
Специальные подклассы сетей Петри
Автоматные
сети.Дляавтоматных сетейвводится ограничение на функции![]() и
и![]() :
:![]() ,
т.е. все переходы имеют одну входную
дугу и одну выходную дугу. Если в начальной
маркировке
,
т.е. все переходы имеют одну входную
дугу и одну выходную дугу. Если в начальной
маркировке![]() есть единственная фишка в некоторой
позиции, то такие сети с
есть единственная фишка в некоторой
позиции, то такие сети с![]() -раскрашиванием
переходов ничем принципиально не
отличаются от так называемых графов
переходов (позиции сети представляют
состояния графа переходов), рассматриваемых
в теории конечных автоматов. Как
следствие, языки таких сетей Петри
являются регулярными. При наличии
большего числа фишек в начальной
маркировке
-раскрашиванием
переходов ничем принципиально не
отличаются от так называемых графов
переходов (позиции сети представляют
состояния графа переходов), рассматриваемых
в теории конечных автоматов. Как
следствие, языки таких сетей Петри
являются регулярными. При наличии
большего числа фишек в начальной
маркировке![]() язык этой сети является «смесью» языков
сетей Петри с тем же графом и с начальными
маркировками
язык этой сети является «смесью» языков
сетей Петри с тем же графом и с начальными
маркировками![]() ,
такими, что
,
такими, что![]()
![]()
![]() .
Напомним, что «смесь» двух формальных
языков
.
Напомним, что «смесь» двух формальных
языков![]() и
и![]() в алфавите
в алфавите![]() определяется так:
определяется так:
![]() ;
;
если
![]() и
и![]() ,
то
,
то
![]()
![]()
![]()
![]() .
.
О чевидно,
что автоматные сети являются ограниченными,
т.к. количество фишек в автоматных сетях
не меняется в результате срабатывания
любого перехода. Из этого, в частности,
следует, что смесь регулярных языков
представляет собой тоже регулярный
язык.
чевидно,
что автоматные сети являются ограниченными,
т.к. количество фишек в автоматных сетях
не меняется в результате срабатывания
любого перехода. Из этого, в частности,
следует, что смесь регулярных языков
представляет собой тоже регулярный
язык.
На рис. 11 приведен пример автоматной сети.
Маркированные графы.Если для некоторой сети Петри выполняется условие:
![]()
то эта сеть называется маркированным графом.
Цикломв маркированном графе называется
«кольцо» переходов![]() ,
такое, что
,
такое, что![]() .
Известны следующие результаты:
.
Известны следующие результаты:
Общее число фишек в позициях, связывающих переходы в цикле, не меняется в результате срабатываний любых переходов.
Переходы в маркированном графе являются живыми, если для каждого его цикла в начальной маркировке есть хотя бы одна фишка в позициях, связывающих переходы этого цикла.
Маркированный граф является безопасной сетью, если для каждого его цикла в начальной маркировке есть ровно одна фишка в позициях, связывающих переходы этого цикла.
М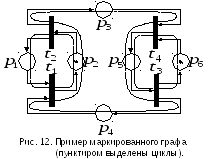 аркированные
графы, как и автоматные сети, представляют
собой ограниченные сети Петри. Как
известно, для таких сетей все задачи их
анализа являются разрешимыми. Однако,
ценой этого является существенная
ограниченность возможностей при
моделировании сложных систем.
аркированные
графы, как и автоматные сети, представляют
собой ограниченные сети Петри. Как
известно, для таких сетей все задачи их
анализа являются разрешимыми. Однако,
ценой этого является существенная
ограниченность возможностей при
моделировании сложных систем.
На рис. 12 приведен пример маркированного графа.
Расширения и обобщения формализма сетей Петри
Обратной стороной простоты и изящества применения формализма сетей Петри при описании относительно простых параллельных систем являются недостатки, проявляющиеся при моделировании более сложных систем. Во-первых, существенным ограничивающим фактором является семантическая монотонность обычных сетей Петри. Во-вторых, абстрактное понимание ресурсов как ничем не отличающихся «фишек» приводит к быстрому росту сложности графа сети при моделировании систем, требующих дифференциации ресурсов. Эти и другие прак тические недостатки базового формализма привели к многочисленным предложениям по его обобщению, модификации и расширению. Рас смотрим некоторые наиболее известные из этих предложений.
Сети
Петри с раскрашенными фишками.
Пусть
![]() - не пустое множество «цветов»
фишек. Для сети Петри с раскрашенными
фишками сохранены определения графа
сети и функции раскрашивания переходов
для задания языков сети. Отличие состоит
в определении понятия начальной
маркировки
- не пустое множество «цветов»
фишек. Для сети Петри с раскрашенными
фишками сохранены определения графа
сети и функции раскрашивания переходов
для задания языков сети. Отличие состоит
в определении понятия начальной
маркировки
![]() сети. Предполагается,
что всякая маркировка сети
сети. Предполагается,
что всякая маркировка сети
![]() определена
как комплект упорядоченных пар позиций
и цветов фишек, соответственно, т.е.
определена
как комплект упорядоченных пар позиций
и цветов фишек, соответственно, т.е.
![]() .
Эквивалентным, но более удобным является
понимание
маркировки как функции
.
Эквивалентным, но более удобным является
понимание
маркировки как функции
![]() ,
сопоставляющей каждой позиции сети
комплект цветов из
,
сопоставляющей каждой позиции сети
комплект цветов из
![]() ,
неформально рассматриваемый как комплект
раскрашенных фишек в этой позиции. Пусть
,
неформально рассматриваемый как комплект
раскрашенных фишек в этой позиции. Пусть
![]() обозначает количество элементов
множества
обозначает количество элементов
множества
![]() в комплекте
в комплекте
![]() :
:
![]() .
Каждому переходу
.
Каждому переходу
![]() сети Петри с раскрашенными фишками
сопоставим некоторую функцию
сети Петри с раскрашенными фишками
сопоставим некоторую функцию
![]() ,
или, в общем случае, бинарное отношение
,
или, в общем случае, бинарное отношение
![]() .
Функция
.
Функция
![]() ,
опредленная ранее для обычных сетей
Петри, для сетей с раскрашенными фишками
обобщается до уровня отношения
,
опредленная ранее для обычных сетей
Петри, для сетей с раскрашенными фишками
обобщается до уровня отношения
![]() следующим образом:
следующим образом:
.
Заметим,
что для всякой пары
![]() комплектов раскра-шенных фишек,
комплектов раскра-шенных фишек,
![]() ,
,
![]() ,
есть
,
есть
![]() вариантов их разбиения на подкомлекты
из заданных количеств раскрашенных
фишек:
вариантов их разбиения на подкомлекты
из заданных количеств раскрашенных
фишек:
![]() ,
,
![]() если
если
![]() и
и![]() для всех
для всех![]() .
.
Другими
словами можно сказать, что значением
![]() для пары - комплекта позиций сети
для пары - комплекта позиций сети
![]() и комплекта цветов фишек
и комплекта цветов фишек
![]() - является число всевозможных комплектов
- является число всевозможных комплектов
![]() пар
пар
![]() комплектов позиций и цветов фишек,
таких, что
комплектов позиций и цветов фишек,
таких, что
![]() и
и
![]() .
.
Если
множество
![]() цветов фишек конечно, то поведение
любой сети с раскрашенными фишками
может быть промоделировано обычной
сетью, в которой каждой позиции
цветов фишек конечно, то поведение
любой сети с раскрашенными фишками
может быть промоделировано обычной
сетью, в которой каждой позиции
![]() исходной сети будет соответствовать
подмножество позиций
исходной сети будет соответствовать
подмножество позиций
![]() ,
а каждому переходу
,
а каждому переходу
![]() - множество переходов, определяемое как
отношением
- множество переходов, определяемое как
отношением
![]() ,
так и возможными разложениями комплектов
раскрашенных входных фишек перехода
на подкомплекты, соответствующие
отдельным позициям. Как правило, в этом
случае, при использовании раскрашенных
фишек хотя и не появляется принципиально
новых возможностей, сложность модели-рующей
сети оказывается существенно меньшей.
,
так и возможными разложениями комплектов
раскрашенных входных фишек перехода
на подкомплекты, соответствующие
отдельным позициям. Как правило, в этом
случае, при использовании раскрашенных
фишек хотя и не появляется принципиально
новых возможностей, сложность модели-рующей
сети оказывается существенно меньшей.
Известны и другие варианты определния сетей Петри с раскрашенными фишками.
С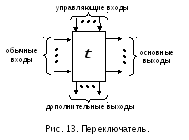 ети
Петри с переключателями.
Вводится новый вид переходов -
«переключателей»,
графически изображаемых так, как показано
на рис.
13.
Такой переход
ети
Петри с переключателями.
Вводится новый вид переходов -
«переключателей»,
графически изображаемых так, как показано
на рис.
13.
Такой переход
![]() имеет комплект обычных входных позиций
и комплект управляющих входных позиций,
а также два комплекта основных и,
соответственно, дополнительных выходных
позиций. Условие срабатывания такого
перехода для маркировки
имеет комплект обычных входных позиций
и комплект управляющих входных позиций,
а также два комплекта основных и,
соответственно, дополнительных выходных
позиций. Условие срабатывания такого
перехода для маркировки
![]() есть условие срабатывания для «обычных»
входных позиций. Если в управляющих
позициях есть необходимые фишки, то
срабатывание перехода приводит, как и
для обычных сетей, к удалению фишек из
всех
входных позиций, а новые фишки появляются
только в основных
выходных
позициях. В противном случае, т.е. если
в управляющих позициях нет необходимого
числа фишек, фишки удаляются только из
обычных входных позиций, а новые фишки
появляются только в дополнительных
выходных позициях.
есть условие срабатывания для «обычных»
входных позиций. Если в управляющих
позициях есть необходимые фишки, то
срабатывание перехода приводит, как и
для обычных сетей, к удалению фишек из
всех
входных позиций, а новые фишки появляются
только в основных
выходных
позициях. В противном случае, т.е. если
в управляющих позициях нет необходимого
числа фишек, фишки удаляются только из
обычных входных позиций, а новые фишки
появляются только в дополнительных
выходных позициях.
Иными
словами, в общем случае в такой сети
заданы не две функции
![]() ,
а четыре:
,
а четыре:![]() ,
задающие для каждого перехода комплекты
обычных входных позиций, управляющих
входных позиций и два комплекта выходных
позиций, основных и дополнительных[.
Условие срабатывания перехода
,
задающие для каждого перехода комплекты
обычных входных позиций, управляющих
входных позиций и два комплекта выходных
позиций, основных и дополнительных[.
Условие срабатывания перехода
![]() при маркировке
при маркировке![]() есть
есть![]() ,
а значение функции переходов при
выполнении этого условия есть
,
а значение функции переходов при
выполнении этого условия есть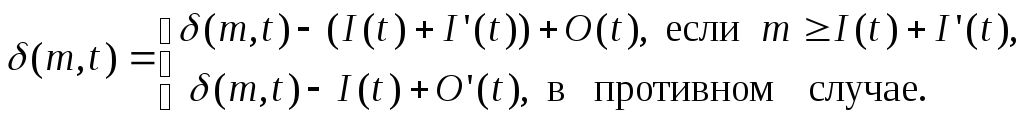
В
случае, если для некоторого
![]()
![]() - пустой комплект (в этом случае комплект
- пустой комплект (в этом случае комплект![]() не влияет на поведение сети, и его тоже
можно считать пустым), то
не влияет на поведение сети, и его тоже
можно считать пустым), то![]() - обычный переход, иначе
- обычный переход, иначе![]() - переключатель (в некоторых работах
без потери принципиальных возможностей
полагают, что для переключателей
- переключатель (в некоторых работах
без потери принципиальных возможностей
полагают, что для переключателей![]() ).
).
Для сетей с переключателями свойство семантической монотонности в общем случае уже не имеет места.
Сети
Петри с ингибиторными дугами.
В таких сетях некоторые входные дуги
переходов (элементы комплектов входных
позиций переходов) могут быть отмечены
как «ингибиторные»
(сдерживающие). Графически такие дуги
изображаются так, как показано на рис.
14. Фактически это означает, что для
переходов в сети задана дополнительно
функция
![]() .
Условие срабатывания перехода
.
Условие срабатывания перехода![]() при маркировке
при маркировке![]() формулируется так:
формулируется так:![]() ,
а значение функции переходов в сети
будет иметь, как и обычно, значение
,
а значение функции переходов в сети
будет иметь, как и обычно, значение
![]() .
Очевидно, что для того, чтобы переход
.
Очевидно, что для того, чтобы переход![]() вообще смог бы сработать хотя бы при
одной маркировке, необходимо, чтобы
выполнялось условие
вообще смог бы сработать хотя бы при
одной маркировке, необходимо, чтобы
выполнялось условие![]() ,
т.е. позиции, связанные с переходом
,
т.е. позиции, связанные с переходом![]() ингибиторными дугами, не должны быть
его обычными входными позициями.
ингибиторными дугами, не должны быть
его обычными входными позициями.
Д ля
сетей с ингибиторными дугами свойство
семантической монотонности, как и для
сетей с переключателями, в общем случае
также не имеет места.
ля
сетей с ингибиторными дугами свойство
семантической монотонности, как и для
сетей с переключателями, в общем случае
также не имеет места.
Сети
Петри с приоритетами.
В таких сетях дополнительно определяется
отношение
приоритетности
переходов
![]() .
Условиями срабатывания перехода
.
Условиями срабатывания перехода![]() при маркировке
при маркировке![]() являются обычное требование
являются обычное требование![]() и дополнительное требование - для этой
маркировки условие срабатывания не
должно быть выполнено для любого более
приоритетного перехода
и дополнительное требование - для этой
маркировки условие срабатывания не
должно быть выполнено для любого более
приоритетного перехода![]() ,
т.е. такого что
,
т.е. такого что![]() .
.
З начение
функции
начение
функции![]() для удовлетворяющих условию срабатывания
переходов в сети определяется обычным
образом.
для удовлетворяющих условию срабатывания
переходов в сети определяется обычным
образом.
Для сетей с приоритетами свойство семантической монотонности в общем случае также не имеет места, так как сети с переключателями и сети с ингибиторными дугами довольно просто моделируются сетями с приоритетами. На рис. 15 и 16 показано, как осуществляется такое моделирование.
С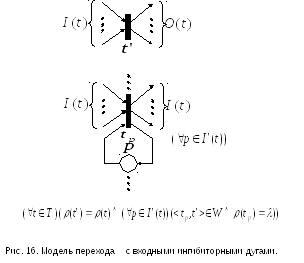 ети
Петри с переходами«исключающее
или».
Наряду с обычными переходами, готовность
к срабатываниям для которых по отношению
к входным дугам реализует дисциплину
«и»,
в сети могут использоваться переходы,
реализующие дисциплину «исключающее
или
»:
переход может сработать, если только в
одной из входных позиций есть фишки, а
в остальных - фишек нет. Если для некоторой
позиции
ети
Петри с переходами«исключающее
или».
Наряду с обычными переходами, готовность
к срабатываниям для которых по отношению
к входным дугам реализует дисциплину
«и»,
в сети могут использоваться переходы,
реализующие дисциплину «исключающее
или
»:
переход может сработать, если только в
одной из входных позиций есть фишки, а
в остальных - фишек нет. Если для некоторой
позиции
![]()
![]() ,
то переход
,
то переход
![]() может сработать при некоторой маркировке
может сработать при некоторой маркировке
![]() ,
если
,
если
![]() ,
а если
,
а если
![]() ,
то - только если
,
то - только если
![]() .
Если
.
Если
![]() ,
то как и для обычных переходов значение
,
то как и для обычных переходов значение
![]() не влияет на возможность срабатывания
перехода
не влияет на возможность срабатывания
перехода
![]() .
Графическое изображение таких переходов
должно каким-то образом отличаться от
графического изображения обычных
переходов (например, оно может быть
таким, как изображено на рис. 17).
.
Графическое изображение таких переходов
должно каким-то образом отличаться от
графического изображения обычных
переходов (например, оно может быть
таким, как изображено на рис. 17).
В се
варианты расширений понятия сети Петри,
в которых условие срабатывания переходов
связано с отсутствием фишек в некоторых
позициях, оказываются равносильными и
настолько расширяющими возможности
формализма сетей Петри, что с использованием
любого из этих вариантов расширения
можно моделировать универсальные
уточнения понятия алгоритма и вычислимой
функции (машины Тьюринга, регистровые
машины, алгорифмы Маркова и т.д.). С другой
стороны, это приводит и к неразрешимости
большинства из теоретических проблем
для расширенных систем, которые являются
полуразрешимыми и даже разрешимыми для
более слабых систем. Для примера покажем,
как сети Петри с ингибиторными дугами
могут моделировать произвольные
регистровые машины.
се
варианты расширений понятия сети Петри,
в которых условие срабатывания переходов
связано с отсутствием фишек в некоторых
позициях, оказываются равносильными и
настолько расширяющими возможности
формализма сетей Петри, что с использованием
любого из этих вариантов расширения
можно моделировать универсальные
уточнения понятия алгоритма и вычислимой
функции (машины Тьюринга, регистровые
машины, алгорифмы Маркова и т.д.). С другой
стороны, это приводит и к неразрешимости
большинства из теоретических проблем
для расширенных систем, которые являются
полуразрешимыми и даже разрешимыми для
более слабых систем. Для примера покажем,
как сети Петри с ингибиторными дугами
могут моделировать произвольные
регистровые машины.
Напомним,
что регистровые машины задаются в форме
специальным образом интерпретированной
стандартной схемы программы с двумя
унарными функциональными символами
![]() ,
,![]() и одним унарным предикатным символом
и одним унарным предикатным символом![]() ,
причем операторы присваивания могут
иметь один из двух видов:
,
причем операторы присваивания могут
иметь один из двух видов:![]() или
или
![]() ,
где
,
где![]() - имя одной из конечного числа ячеек
памяти («регистров»). Один или несколько,
что не принципиально, регистров объявлены
как входные (их начальные значения -
исходные данные), а один или несколько,
возможно других, регистров объявлены
как выходные (их заключительные значения
- результаты работы машины). Интерпретация
- имя одной из конечного числа ячеек
памяти («регистров»). Один или несколько,
что не принципиально, регистров объявлены
как входные (их начальные значения -
исходные данные), а один или несколько,
возможно других, регистров объявлены
как выходные (их заключительные значения
- результаты работы машины). Интерпретация![]() такова: область интерпретации
такова: область интерпретации![]() - множество
- множество![]() натуральных чисел,
натуральных чисел,![]()
![]()
=
=
![]() ,
,![]()
![]()
=
=![]() ,
,![]()
![]()
=
=![]() .
Известно, что для любой частично-рекурсивной
функции можно построить вычисляющую
ее значения регистровую машину.
.
Известно, что для любой частично-рекурсивной
функции можно построить вычисляющую
ее значения регистровую машину.
Пусть задана конкретная регистровая машина. Построим сеть Петри с ингибиторными дугами по следующим правилам:
множество позиций
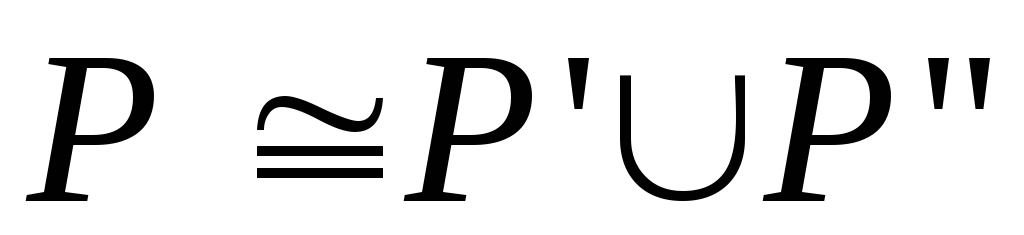 ,
где
,
где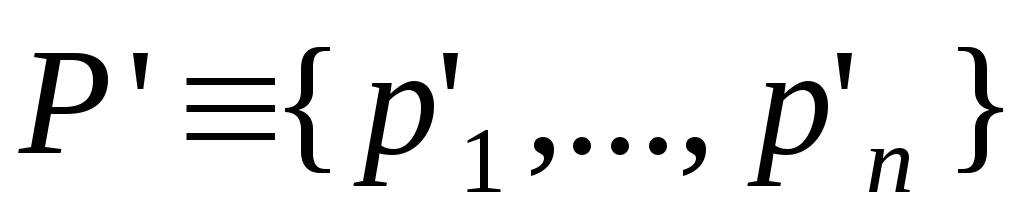 - подмножество позиций, сопоставленных
регистрам машины, а
- подмножество позиций, сопоставленных
регистрам машины, а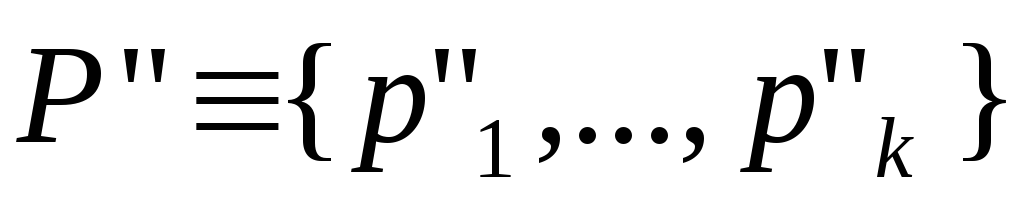 - подмножество позиций, сопоставленных
вершинам управляющего графа схемы
программы;
- подмножество позиций, сопоставленных
вершинам управляющего графа схемы
программы;начальная маркировка
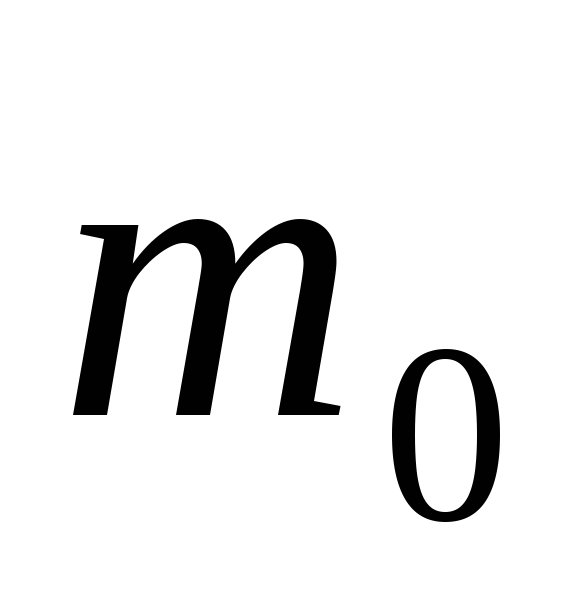 такова:
такова: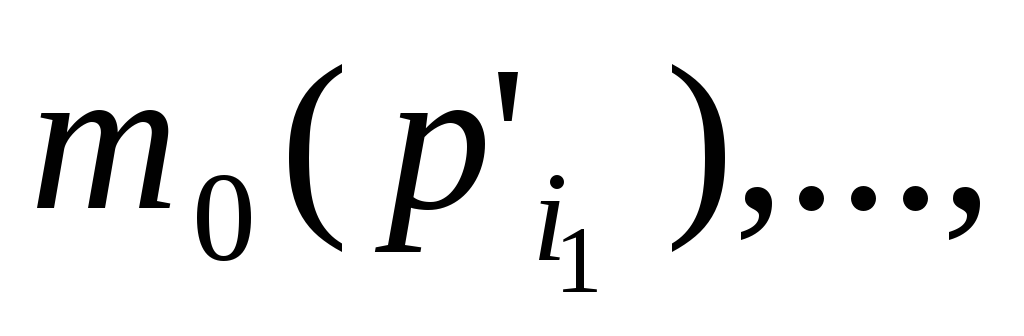
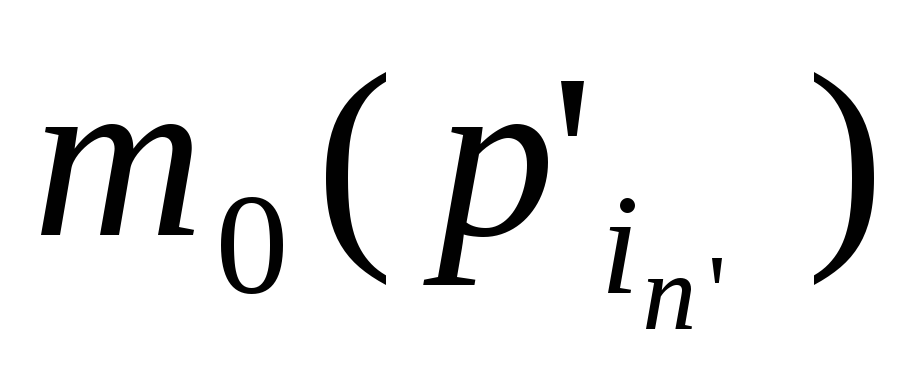 - исходные данные, где
- исходные данные, где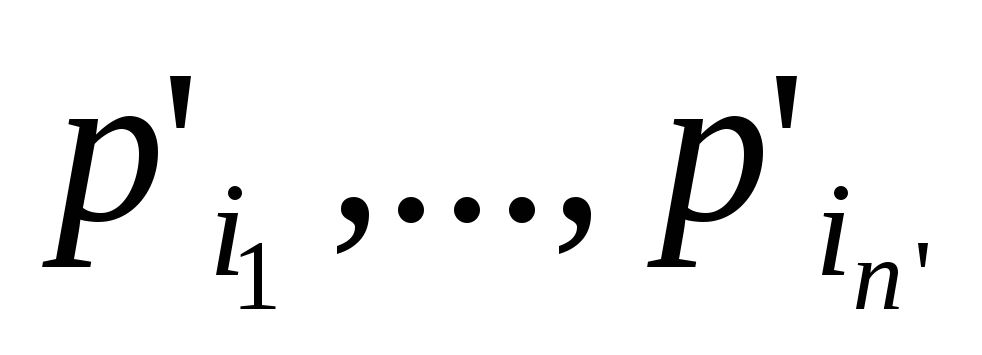 - позиции, сопоставленные входным
регистрам
- позиции, сопоставленные входным
регистрам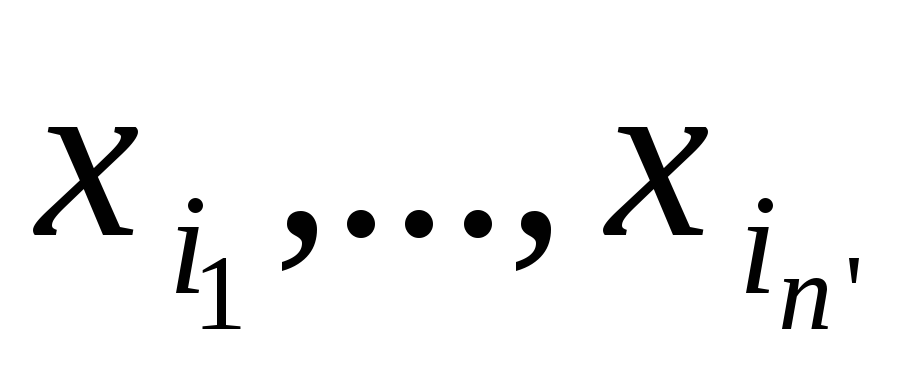 ;
;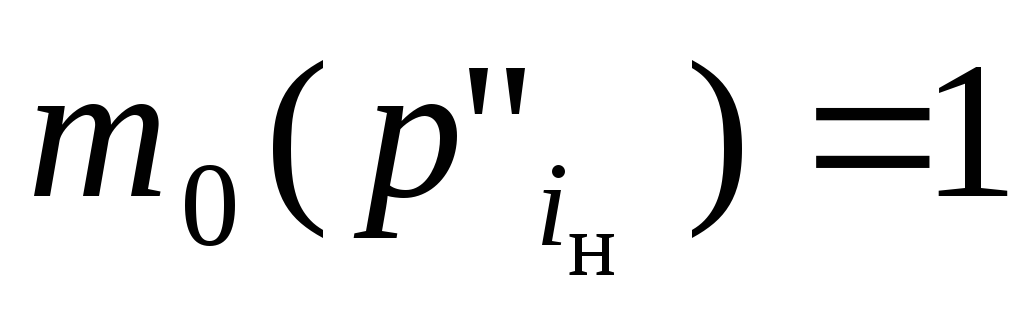 ,
где
,
где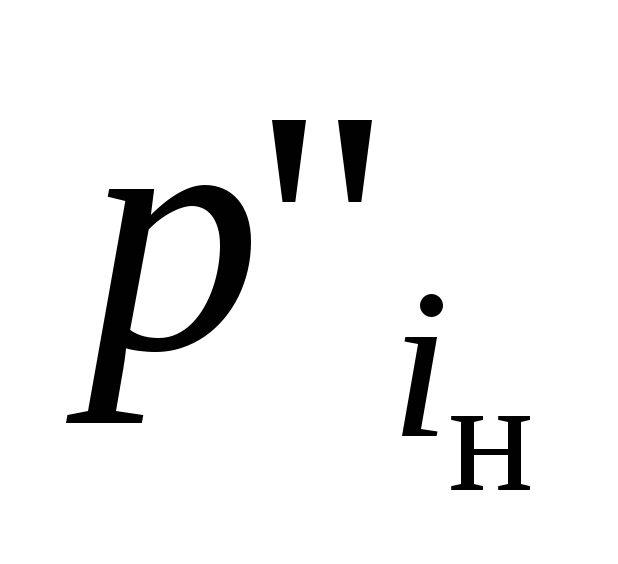 - позиция, сопоставленная начальному
блоку управляющего графа схемы программы,
а для всех остальных позиций
- позиция, сопоставленная начальному
блоку управляющего графа схемы программы,
а для всех остальных позиций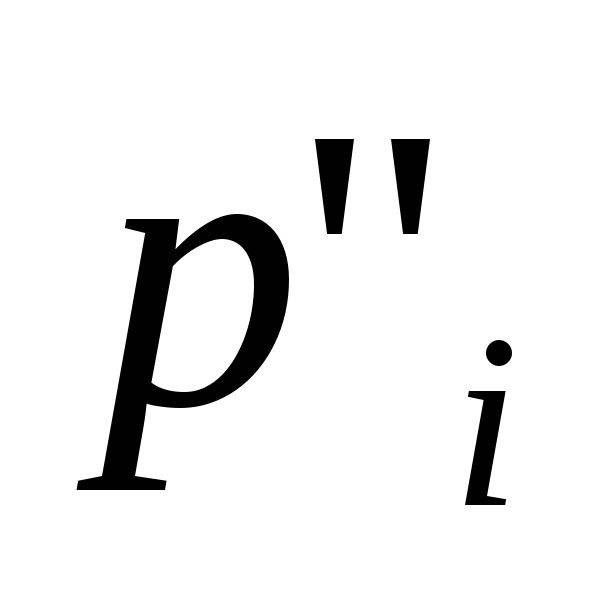 ,
,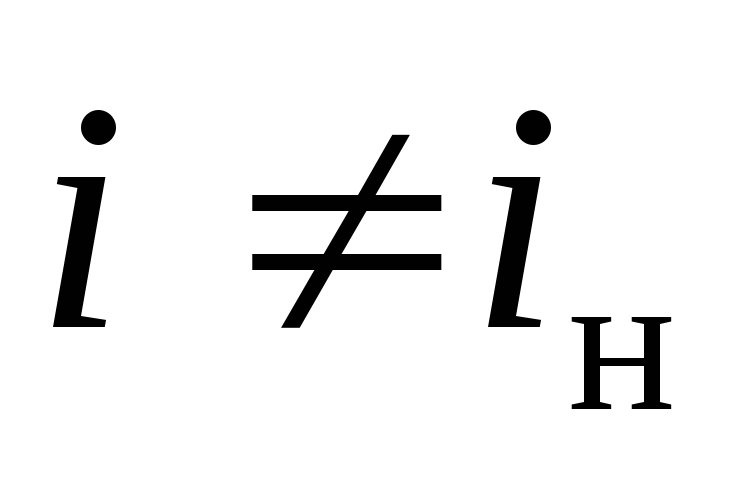 ,
,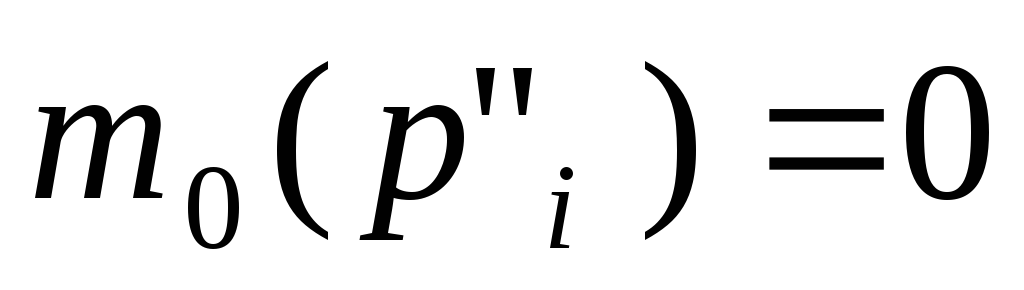 ;
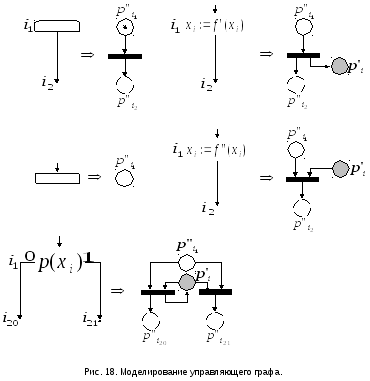
;построение переходов сети иллюстрирует рис. 18. На нем показана трансляция начального и заключительного блока, блоков присваивания и блоков ветвления программы.
Очевидно, что для определенной таким образом сети Петри либо
существует единственная история срабатываний переходов, приводящая сеть к тупиковой маркировке
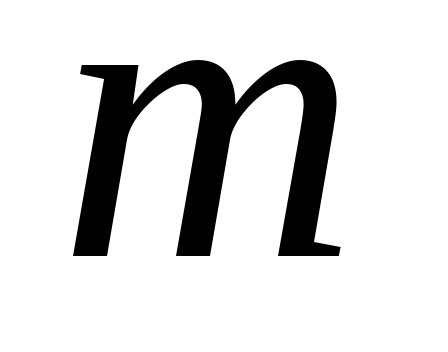 ,
для которой
,
для которой
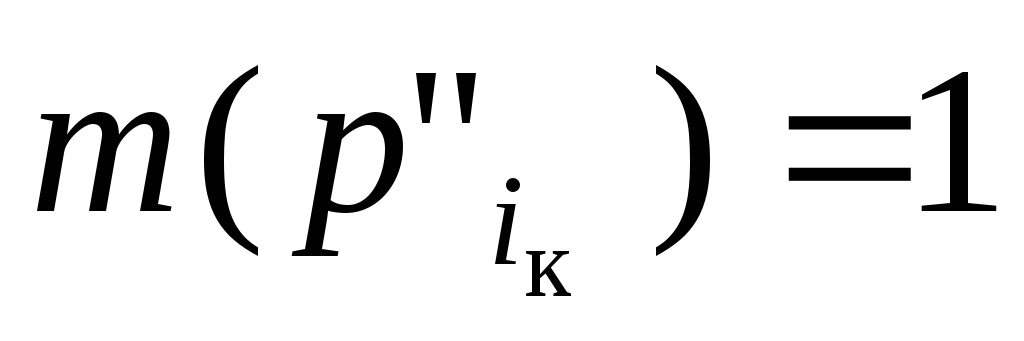 ,
где
,
где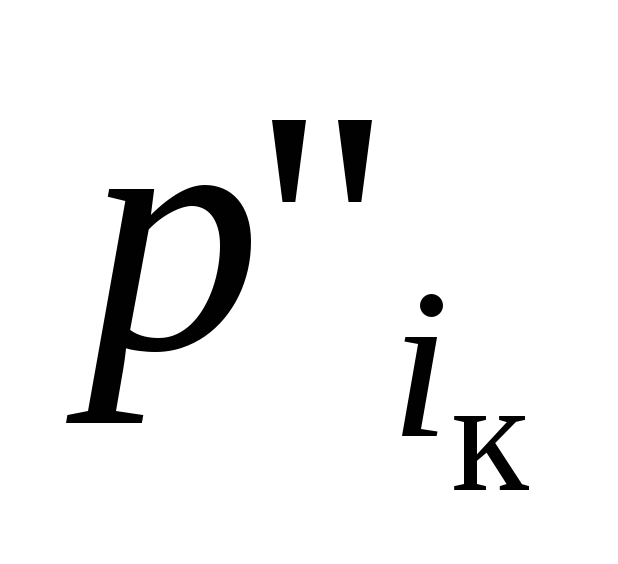 - позиция, сопоставленная заключительному
блоку управляющего графа схемы программы,
а для всех остальных позиций
- позиция, сопоставленная заключительному
блоку управляющего графа схемы программы,
а для всех остальных позиций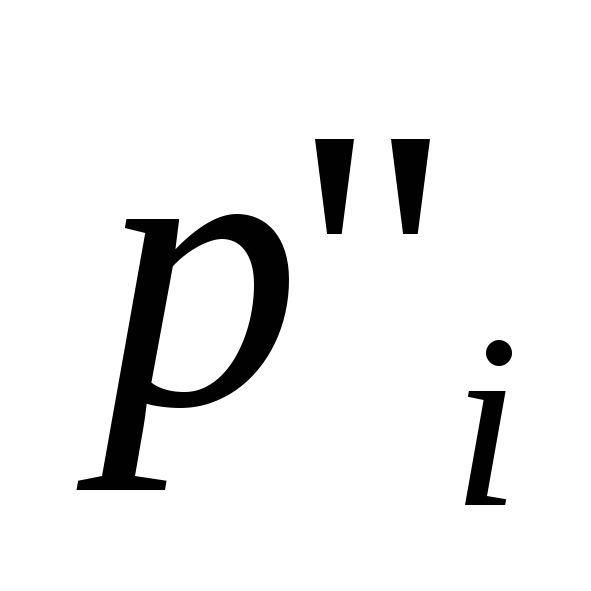 ,
,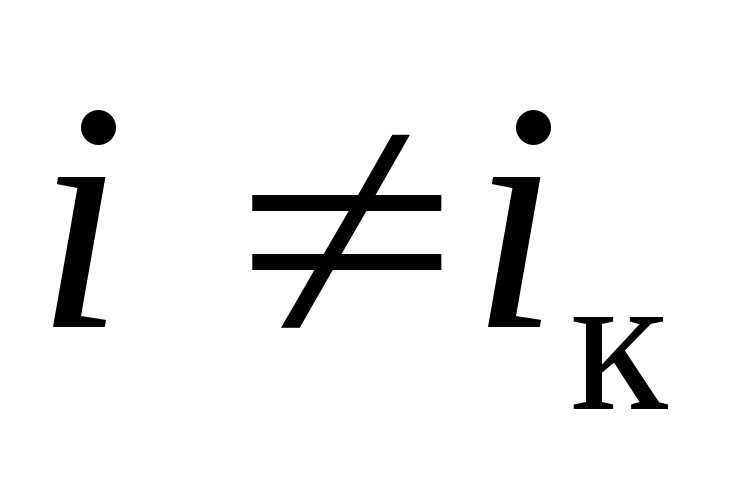 ,
,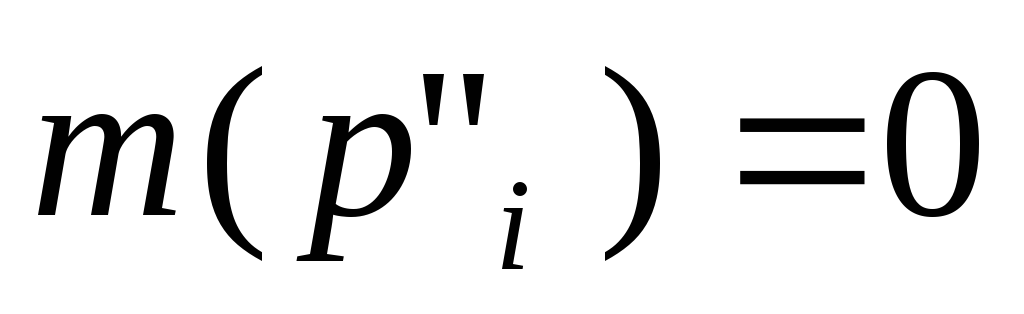 .
.
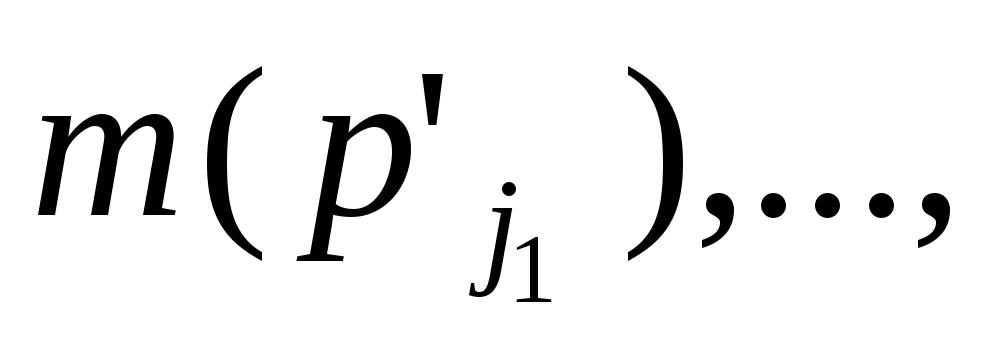
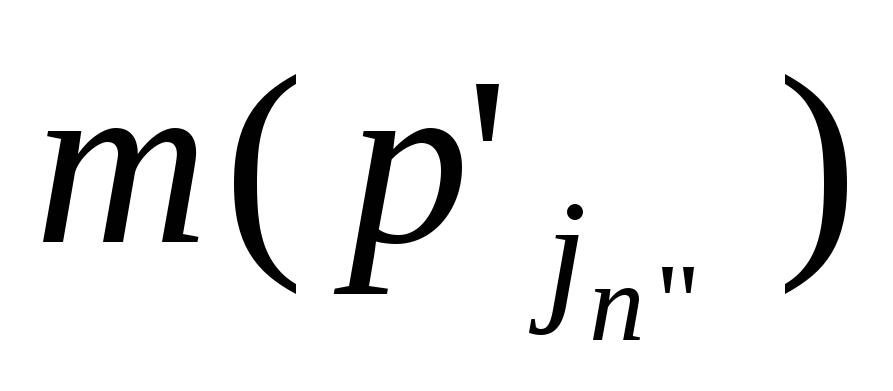 - результаты
работы регистровой машины, где
- результаты
работы регистровой машины, где
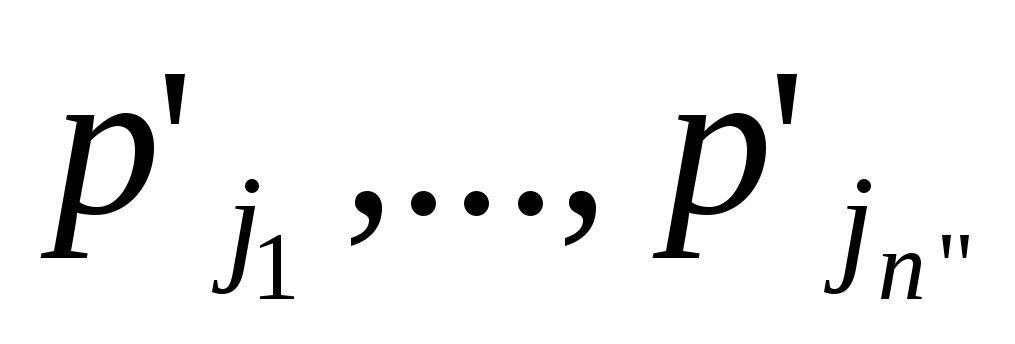 - позиции, сопоставленные выходным
регистрам
- позиции, сопоставленные выходным
регистрам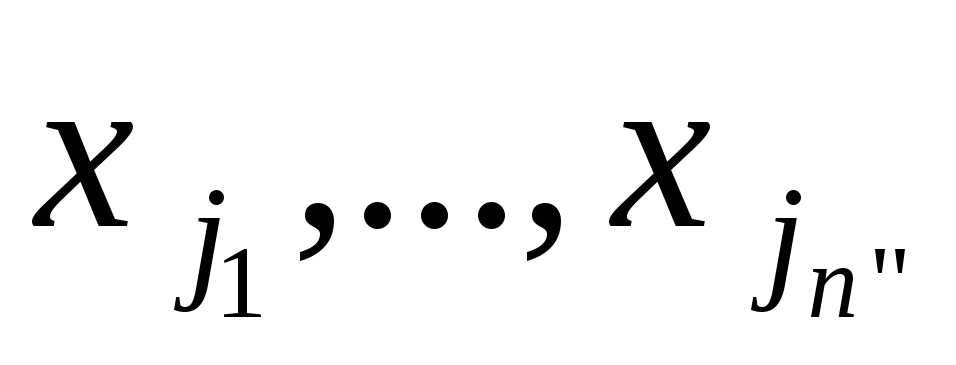 ,
либо
,
либос
 уществует
единственная, потенциально не ограниченная
история срабатываний переходов, не
приводящая сеть к тупиковой маркировке.
В этом случае результаты работы
регистровой машины не определены.
уществует
единственная, потенциально не ограниченная
история срабатываний переходов, не
приводящая сеть к тупиковой маркировке.
В этом случае результаты работы
регистровой машины не определены.
