Сети Петри.

Сетью Петри принято называть тройку , где– граф сети Петри, – конечное множествопозиций (или мест) сети, – конечное множествопереходов сети, ;– функции, задающие комплектывходных и, соответственно, выходных позиций переходов сети (здесь – множество всевозможных конечныхкомплектов элементов множества );-начальная маркировка (разметка) позиций сети, - множество всевозможныхмаркировок; –функция раскраски, где – множествокрасок.

Пользуясь терминологией теории графов, можно сказать, что сети Петри – двудольные мультиорграфы с вершинами двух сортов (позициями, помеченными натуральными числами согласно начальной маркировке, и переходами, помеченными элементами множества согласно функции раскраски). Позиции как вершины графа изображаются в форме кружков, а переходы – в форме линий («полок»), обычно утолщенных. В кружке, соответствующем позиции , значениеизображается либо в форме записи числа в десятичной системе счисления, либо в форме жирных точек («фишек») в количествештук. Метки переходов изображаются рядом с соответствующими «полками».

Обычно в качестве возможных красок допускаются или отдельные буквы, или слова (например, любые или только пустое слово и все однобуквенные слова), или множества слов (например, регулярные или рекурсивные множества слов) в некотором конечном алфавите. Будем далее предполагать, что, в общем случае, – формальный язык, интерпретированный на классе множеств слов в алфавите. Если,– тождественная функция, а буквакак элемент языкаинтерпретируется традиционно как множество слов, включающее единственное однобуквенное слово, то сеть Петри называетсясвободно раскрашенной.

Сети Петри, как правило, рассматриваются с точностью до изоморфизма, то есть имена позиций и переходов являются «связанными» внутри сети и при графическом изображении, вообще говоря, могут не указываться (они необходимы только для ссылок, например, при описании поведения сети):

Определение 1. Сети и, считаютсяидентичными, если существуют взаимно-однозначные отображения и, такие, что.

Основой определения семантики сетей Петри является функция переходов , в общем случае частичная:Здесь «+» и «-» – знаки операций «сложения» и «вычитания» комплектов: ,, где. Функцияобобщается на множество кортежей переходов ():,.Мно-жество маркировок, достижимых из маркировки , обозначается и определяется так: , а множество всех достижимых в сети маркировок (достижимых из начальной маркировки ) так: . Маркировка называетсятупиковой, если для всех не определено, т.е. не выполняется условие.обозначает подмножество всехдостижимых тупиковых маркировок в сети. Кортеж переходов называется историей достижения маркировки , если. Множество всех возможных историй достижения маркировкиобозначим.

Переходы могут классифицироваться по степени их «активности»:

1. «мертвый» переход (не встречается ни в одной истории достижения маркировок из );

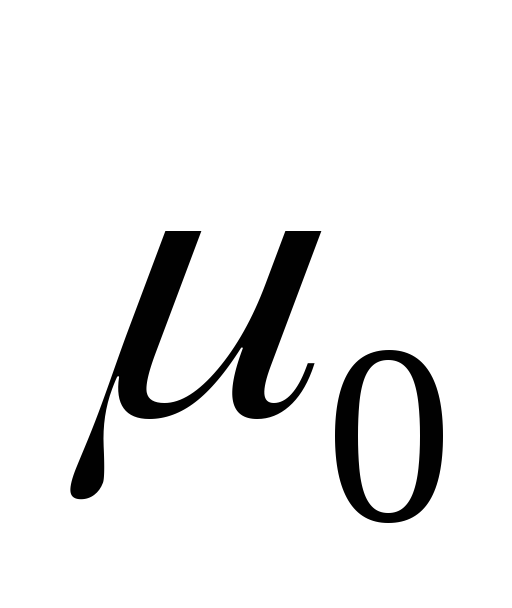2. «потенциально мертвый» переход (существуют маркировки, ни в одно из продолжений историй достижения которых он не входит);

3. «потенциально живой» переход, который входит в хотя бы одну из историй достижения некоторой маркировки из ;

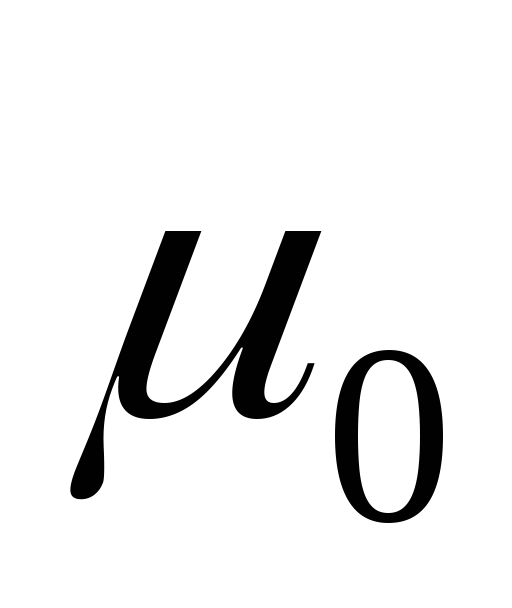4. «живой» переход (входит в одно из продолжений любой истории достижения маркировок из );

5. переход, который входит в некоторую историю достижения маркировок из не менее любого заданного числа раз;

6. переход, для которого существует бесконечная последовательность продолжающих друг друга историй достижения маркировок из , в которые он входит бесконечное число раз.

Сеть называется безопасной, если . Очевидно, что безопасные сети могут быть реализованы логическими схемами с двоичными элементами памяти, представляющими отдельные позиции этой сети.

Сеть называется ограниченной, если . Также очевидно, что ограниченные сети могут быть реализованы конечными автоматами.

Проблема ограниченности сети является разрешимой, то есть для любой сети Петри можно за конечное число шагов определить, является она ограниченной или нет.

• Деревом достижимости сети Петри называется дерево, вершины которого помечены обобщенными маркировками , для которых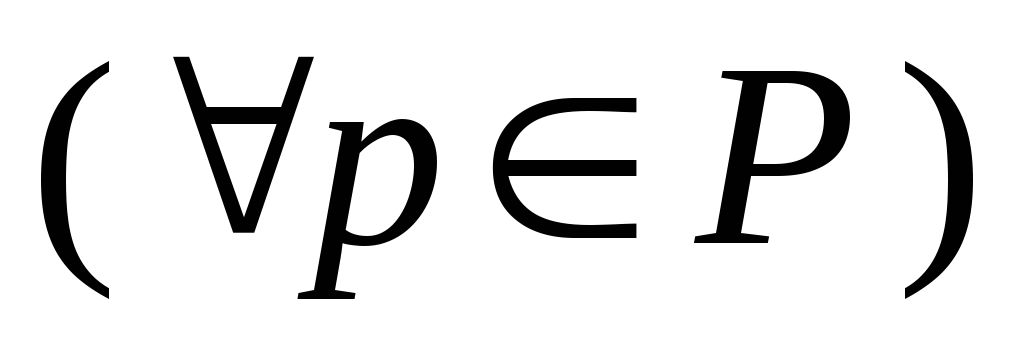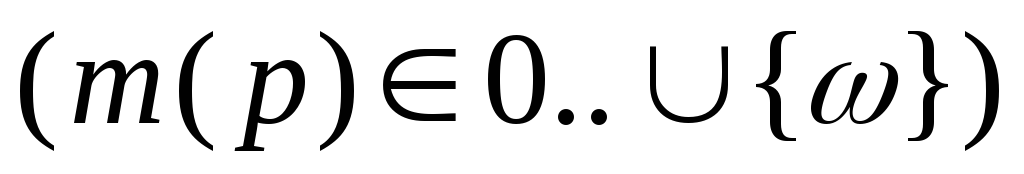. Символобозначает сколь угодно большое число (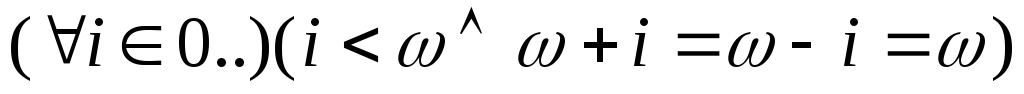). Корневая вершина дерева достижимости помечена начальной маркировкой, а дуги, исходящие из вершины, помеченной маркировкой, помечены всеми возможными переходами, которые могут сработать при маркировке(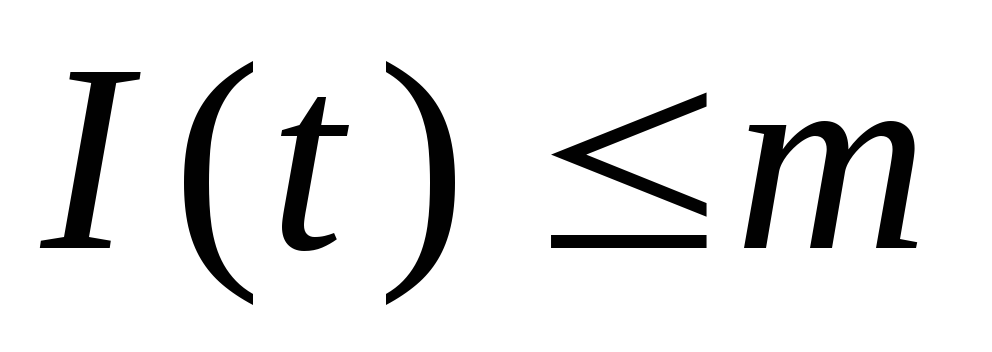), и ведут, соответственно, в вершины, помеченные маркировками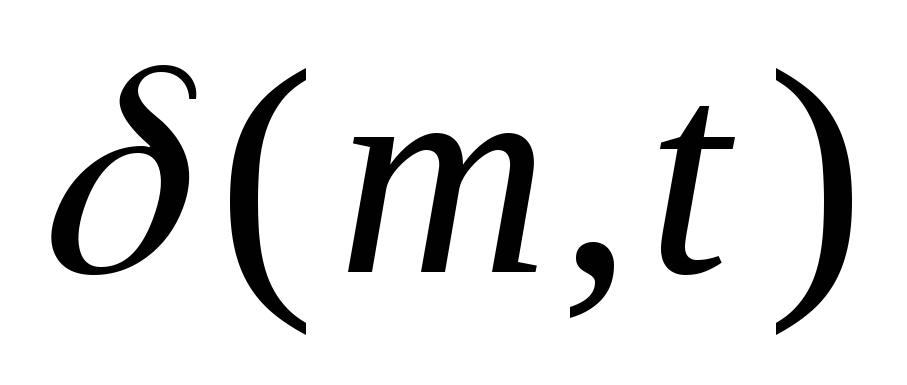. Если в ветви, идущей из корня дерева к маркировке, встречается маркировка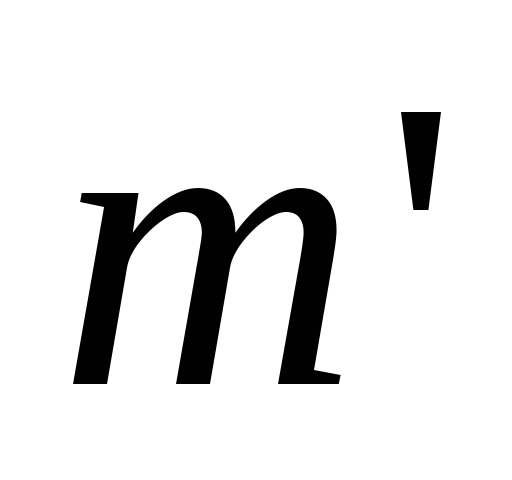, строго меньшая маркировки, то для всех позиций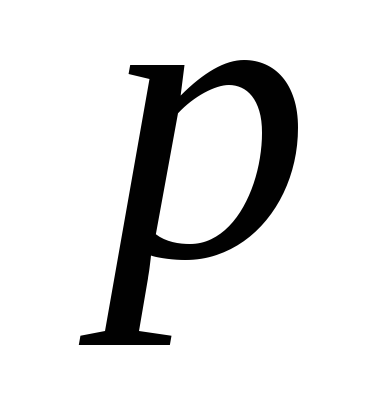, для которых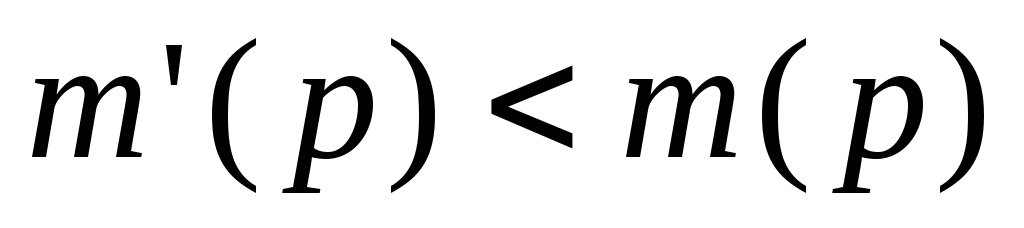, полагаем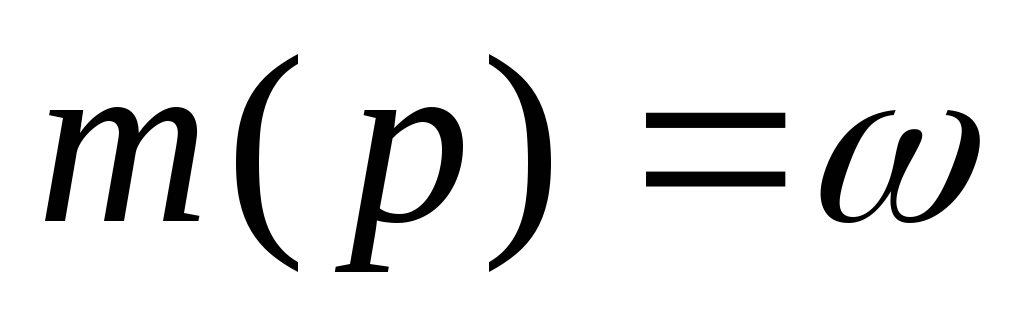. 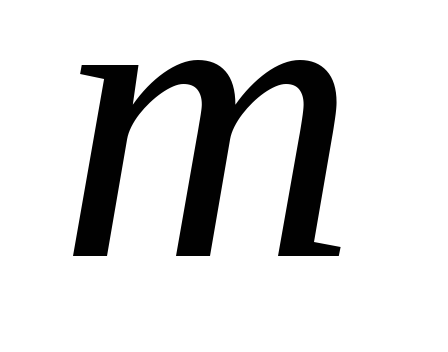Это означает, что количество фишек в этих позициях в достижимых измаркировках может быть сколь угодно большим. Построение дерева достижимости обрывается в следующих двух случаях:

• если вершина помечена обобщенной маркировкой, являющейся тупиковой,

• если в некоторой ветви, идущей из корня дерева, повторно встречается одна и та же обобщенная маркировка.

Доказательство конечности дерева достижимости любой сети Петри базируется на следующих леммах.

Лемма 1. В любом бесконечном направленном дереве с конечными степенями вершин существует бесконечный путь, исходящий из корня.

Лемма 2. Всякая бесконечная последовательность натуральных чисел содержит бесконечную неубывающую подпоследовательность.

Лемма 2. Всякая бесконечная последовательность обобщенных комплектов элементов конечного множества (кратности могут иметь значение ) содержит бесконечную неубывающую подпоследовательность.

Доказательство лемм достаточно очевидно, а доказательство теоремы о конечности дерева достижимости проводится от противного.

Другой вариант доказательства базируется на следующей теореме:

Теорема. Для всякого конечного множества не существует бесконечных множеств попарно не сравнимых обобщенных комплектов его элементов.

Таким образом, построение дерева достижимости для любой сети Петри всегда завершается за конечное число шагов. Следовательно, проблема ограниченности сети является разрешимой: если ни одна из обобщенных маркировок в дереве достижимости не использует значение , то сеть является ограниченной, а в противном случае – нет.

На рис. 1 показан пример сети с заданной начальной маркировкой и построено для нее дерево достижимости.

Дерево достижимости в общем случае не определяет однозначно множество достижимых маркировок. На рис. 2 показаны две разные сети Петри, имеющие одно и то же дерево достижимости, хотя для первой из них существуют достижимые маркировки с любым количеством фишек в позиции , а во второй во всех достижимых маркировках в этой позиции может быть только четное количество фишек.