
Рекурсивные функции
.docРЕКУРСИВНЫЕ ФУНКЦИИ
Рекурсивной
функцией
(РФ) принято называть вычислимую функцию,
аргументы и значения которой суть
натуральные числа из
![]() . Вычислимость понимается интуитивно
как существование эффективных правил
вычисления значения функции по заданным
значениям аргументов из области ее
определения. Теории рекурсивных функций
были одними из первых формальных
уточнений понятия вычислимости. Попытки
построения формальных теорий, описывающих
подкласс
. Вычислимость понимается интуитивно
как существование эффективных правил
вычисления значения функции по заданным
значениям аргументов из области ее
определения. Теории рекурсивных функций
были одними из первых формальных
уточнений понятия вычислимости. Попытки
построения формальных теорий, описывающих
подкласс
![]() общерекурсивных
функций -
всюду определенных рекурсивных функций,
были обречены на неудачу, так как
множество всех ОРФ не является
рекурсивно-перечислимым.
общерекурсивных
функций -
всюду определенных рекурсивных функций,
были обречены на неудачу, так как
множество всех ОРФ не является
рекурсивно-перечислимым.
Для
доказательства этого (от противного)
используется диагональный метод Кантора.
Действительно, предположим, что множество
![]() всех
ОРФ является рекурсивно-перечислимым.
Иными словами, существует вычислимая,
всюду определенная на натуральных
числах «нумерующая» функция
всех
ОРФ является рекурсивно-перечислимым.
Иными словами, существует вычислимая,
всюду определенная на натуральных
числах «нумерующая» функция
![]() ,
областью значений которой является
множество
,
областью значений которой является
множество
![]() .
Определим функцию
.
Определим функцию
![]() .
Очевидно, что функция
.
Очевидно, что функция
![]() при сделанном допущении является
общерекурсивной, т.е. вычислимой и всюду
определенной на натуральных числах.
Так как
при сделанном допущении является
общерекурсивной, т.е. вычислимой и всюду
определенной на натуральных числах.
Так как
![]() ,
то существует такое число
,
то существует такое число
![]() ,
что
,
что
![]() .
Рассмотрим значение
.
Рассмотрим значение
![]() .
С одной стороны, согласно последнему
утверждению,
.
С одной стороны, согласно последнему
утверждению,
![]() .
С другой стороны, по определению функции
.
С другой стороны, по определению функции
![]() ,
,
![]() .
Так как речь идет об одном и том же
конкретном натуральном числе, получим
противоречие, опровергающее исходное
предположение о том, что множество всех
ПРФ является рекурсивно-перечислимым.
.
Так как речь идет об одном и том же
конкретном натуральном числе, получим
противоречие, опровергающее исходное
предположение о том, что множество всех
ПРФ является рекурсивно-перечислимым.
Отсюда следует, что множество ОРФ не может быть определено дедуктивной формальной теорией, множество теорем которой всегда рекурсивно-перечислимо. В то же время, множество всех рекурсивных функций, в том числе и не всюду определенных, согласно тезису А.Черча1, допускает подобную формализацию, известную как теория частично-рекурсивных функций (ЧРФ). Элементы этой теории (теоремы) называются схемами ЧРФ. Аксиомами являются атомарные схемы, интерпретируемые как всюду определенные «базисные» рекурсивные функции. Простейшие правила вывода интерпретируются как способы композиции ЧРФ. Известно несколько равносильных вариантов уточнения этой теории, отличающихся выбором набора базисных функций и деталями определения способов их композиции.
-
Базисные функции:
![]() ,
где
,
где
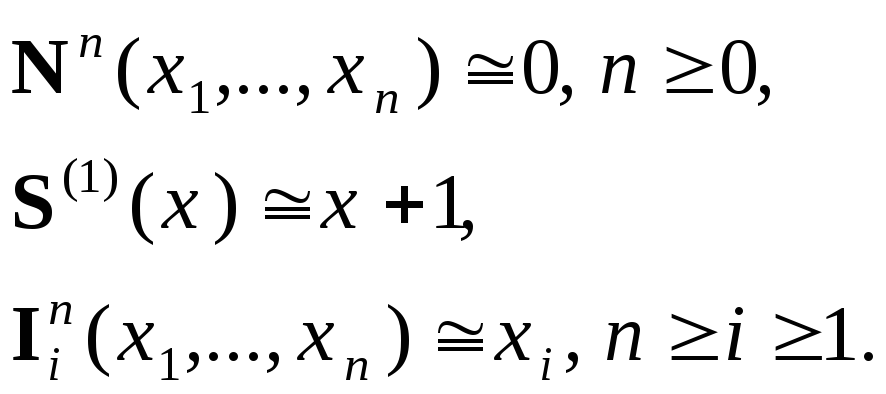
Способы композиции:
примитивная рекурсия
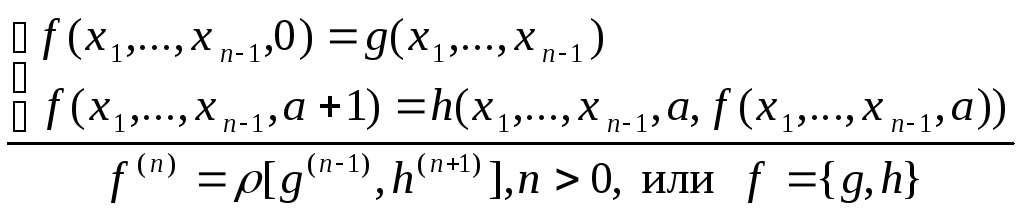 ;
;
суперпозиция
![]() ;
;
оператор
минимизации (![]() -оператор)
-оператор)
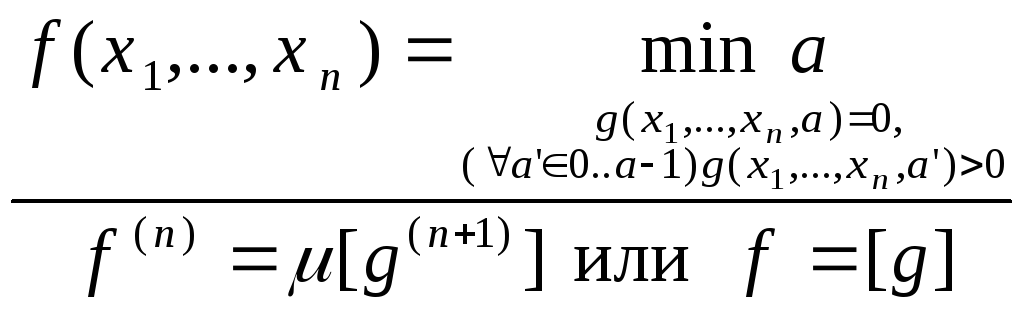 .
.
-
Базисные функции:
![]() ,
где
,
где
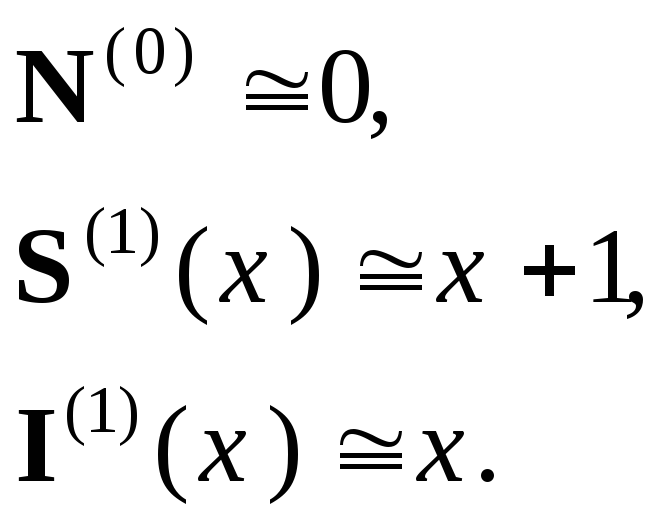
Способы композиции:
введение фиктивного аргумента справа
![]() ,
,
введение фиктивного аргумента слева
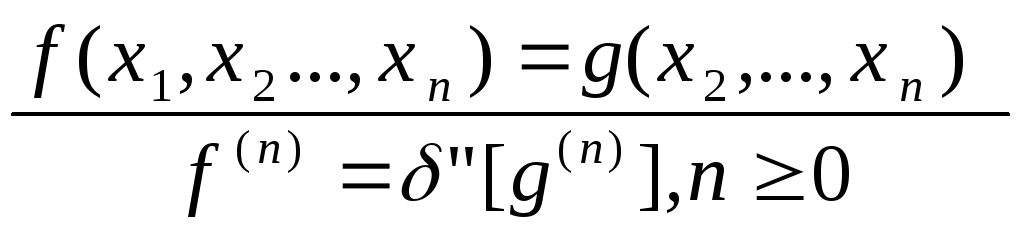 ,
,
примитивная рекурсия
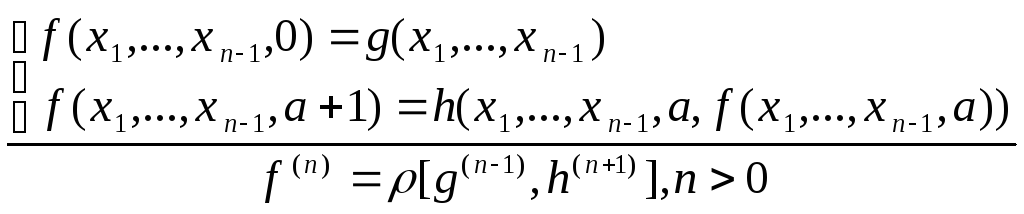 ;
;
суперпозиция
![]() ;
;
оператор
минимизации (![]() -оператор)
-оператор)
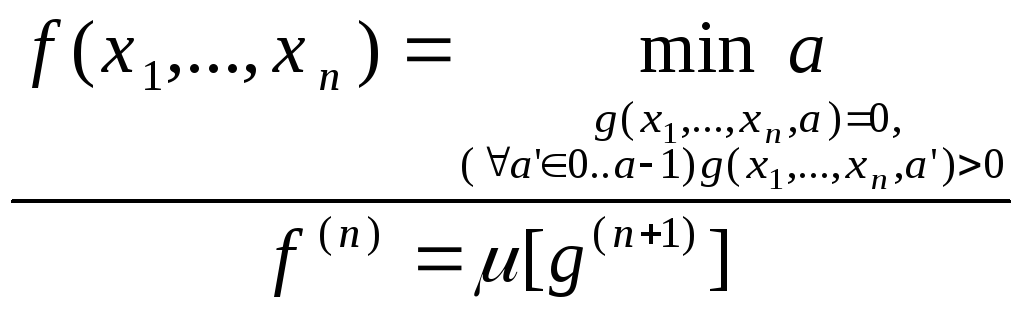 .
.
Нумерация чрф.
Принципы нумерации рекурсивно определенных конструктивных множеств описаны в соответствующем разделе пособия.
Пусть «![]() »
»![]() обозначает номер чрф
обозначает номер чрф
![]() среди всех чрф арности
среди всех чрф арности
![]() .
Определение этих номеров распадается
на три случая:
.
Определение этих номеров распадается
на три случая:
![]() ,
,
![]() и
и
![]() .
.
![]() :
:
«![]() »
»![]() ,
,
«![]() »
»![]() «
«![]() »
»![]() «
«![]() »
»![]() «
«![]() »
»![]() ,
,
«![]() »
»![]() «
«![]() »
»![]() .
.
![]() :
:
«![]() »
»![]() ,
,
«![]() »
»![]() ,
,
«![]() »
»![]() ,
,
«![]() »
»![]() «
«![]() »
»![]() «
«![]() »
»![]() «
«![]() »
»![]() ,
,
«![]() »
»![]() «
«![]() »
»![]() ;
;
«![]() »
»![]() «
«![]() »
»![]() «
«![]() »
»![]() .
.
Для любых
![]() :
:
«![]() »
»![]() ,
,
«![]() »
»![]() ,
,
![]() ,
,
«![]() »
»![]() «
«![]() »
»![]() «
«![]() »
»![]() «
«![]() »
»![]() ,
,
«![]() »
»![]() «
«![]() »
»![]() ;
;
«![]() »
»![]() «
«![]() »
»![]() «
«![]() »
»![]() .
.
Универсальная функция :
![]() «
«![]() »
»![]() ,
где «
,
где «![]() »
»![]() - номер чрф
- номер чрф
![]() среди всех чрф арности
среди всех чрф арности
![]() .
.
Пусть универсальная
функция
![]() реализуется универсальным вычислителем
с нижеследующим алгоритмическим
описанием:
реализуется универсальным вычислителем
с нижеследующим алгоритмическим
описанием:

Здесь
![]() - некоторые прф. Тогда функция
- некоторые прф. Тогда функция
![]() может быть описана как чрф:
может быть описана как чрф:
![]() ,
где
,
где
![]() ,
то есть
,
то есть
![]() .
.
Действительно,
![]() ,
где
,
где
![]() наименьшее
наименьшее
![]() ,
такое, что
,
такое, что
![]() .
.
ТЕОРИЯ УНАРНЫХ ЧРФ
Все учрф интерпретируются как частичные вычислимые функции одного аргумента.
Базисные учрф:
![]() ,
интерпретируемые как всюду определенные
функции:
,
интерпретируемые как всюду определенные
функции:
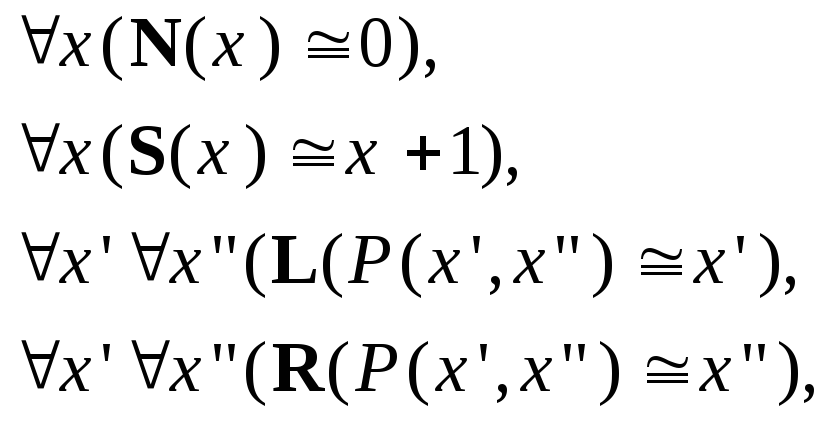
где
![]() - произвольная функция нумерации
упорядоченных пар натуральных чисел,
монотонно возрастающая по обоим
аргументам, т.е.
- произвольная функция нумерации
упорядоченных пар натуральных чисел,
монотонно возрастающая по обоим
аргументам, т.е.
![]() (очевидно, что
(очевидно, что
![]() ).
).
Способы композиции:
композиция
![]() ;
;
суперпозиция
![]() ();
();
![]() -оператор
-оператор
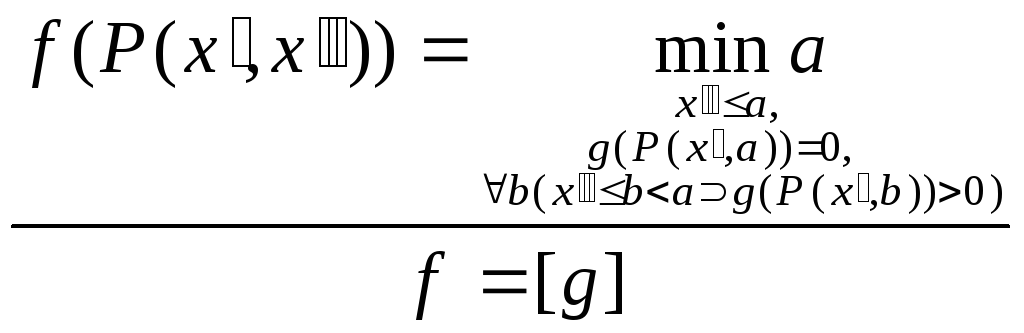 ;
;
оператор
примитивной рекурсии
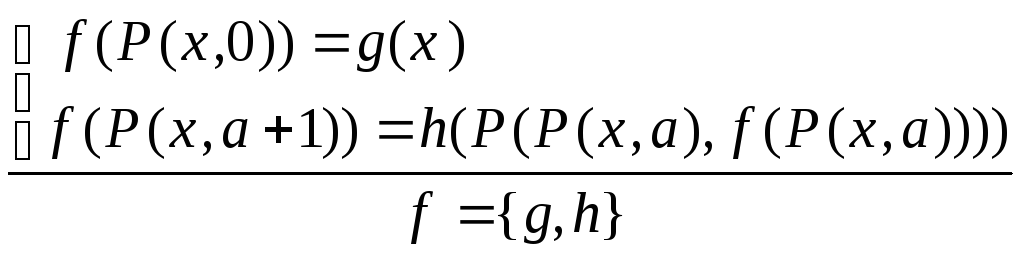 .
.
Определения:
![]() (легко вывести,
что
(легко вывести,
что
![]() ).
).
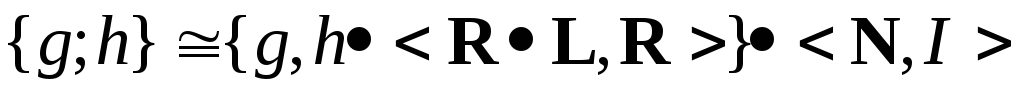 ,
т.е.
,
т.е.
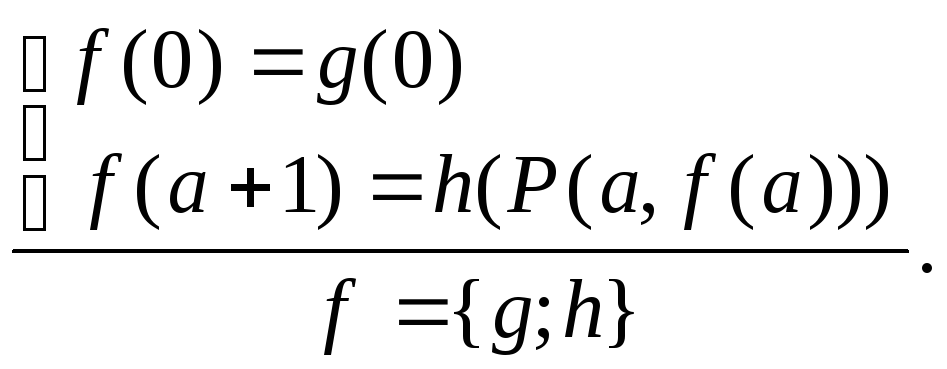
![]() (расстановка
скобок в сложной композиции).
(расстановка
скобок в сложной композиции).
![]()
(легко вывести,
что
![]() ,если
,если
![]() - определено).
- определено).
Приоритет операции
![]() ниже, чем приоритет операции
ниже, чем приоритет операции
![]() .
.
![]() (как показано
далее, оператор суперпозиции является
ассоциативным, и, следовательно,
расстановка скобок в сложной суперпозиции
не играет роли).
(как показано
далее, оператор суперпозиции является
ассоциативным, и, следовательно,
расстановка скобок в сложной суперпозиции
не играет роли).
![]() (
(![]() - всюду не определенная функция).
- всюду не определенная функция).
![]() (
(![]() ).
).
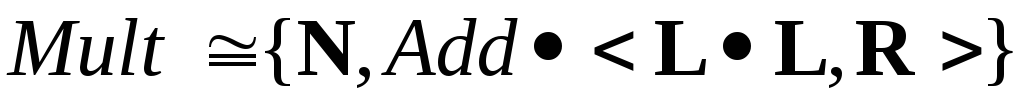 (
(![]() ).
).
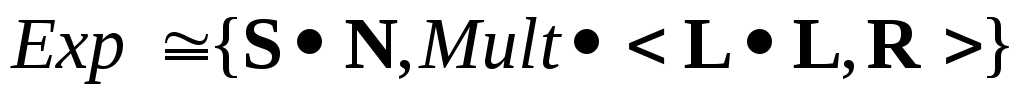 (
(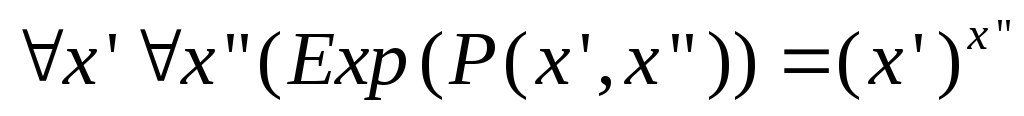 ,
,
![]() ).
).
![]() (
(![]() ,
т.е.
,
т.е.
![]() ).
).
![]() (
(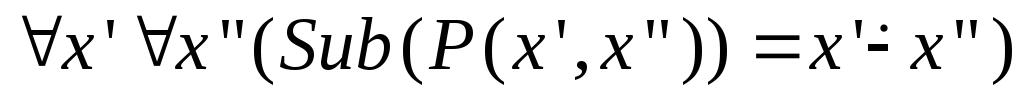 ,
т.е. если
,
т.е. если
![]() ,
то
,
то
![]() ,
иначе
,
иначе
![]() ).
).
Пусть для любой
строго монотонной ОРФ
![]() обратная функция
обратная функция
![]() определяется так:
определяется так:
![]() .
.
Тогда
![]() ,
где
,
где
![]() ,
то есть
,
то есть
![]()
(заметим, что
![]() ).
).
Для
любой функции
![]() определим «итерированную» функцию
определим «итерированную» функцию
![]() ,
такую, что
,
такую, что
![]() :
:
![]() .
.
![]() ,
где
,
где
![]() (заметим,что
(заметим,что
![]() - функция упорядоченной пары натуральных
чисел диагональным методом нумерации,
т.е.
- функция упорядоченной пары натуральных
чисел диагональным методом нумерации,
т.е.
![]() ,
а значение
,
а значение
![]() есть количество элементов в таблице
значений функции
есть количество элементов в таблице
значений функции
![]() ,
находящихся левее и выше диагонали с
номером
,
находящихся левее и выше диагонали с
номером
![]() ).
).
![]() .
.
![]() .
.
Очевидно, что
![]() .
.
Эквивалентность учрф.
Пусть
![]() - метапеременные, множество значений
которых составляют произвольные учрф.
- метапеременные, множество значений
которых составляют произвольные учрф.
Аксиома
1:![]() .
.
Аксиома
2:
![]()
Аксиома
3:
![]()
Аксиома
4:
![]()
Аксиома
5:
![]()
Аксиома
6:
![]()
Аксиома
7:
![]()
Аксиома
8:![]() .
.
Аксиома
9:![]() .
.
Теорема
1:![]() .
.
Аксиома
10:![]() .
.
Аксиома
11:![]() .
.
Аксиома
12:![]() .
.
Теорема
2:
![]() .
.
Доказательство:
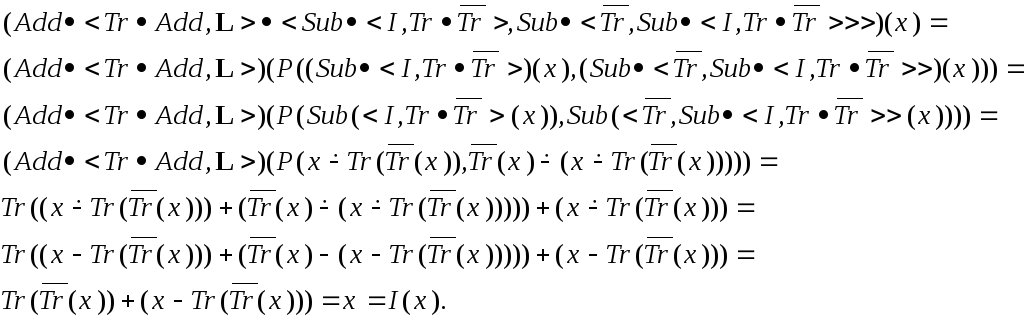 Аксиома
13:
Аксиома
13:
![]() .
.
Аксиома
14:
![]() .
.
Аксиома
15:
![]() .
.
Теорема
3:
![]() .
.
Теорема
4:
![]() .
.
Теорема
5:
![]() .
.
Нумерация учрф.
Пусть «![]() »
обозначает номер учрф
»
обозначает номер учрф
![]() .
Тогда
.
Тогда
«![]() »
»![]() ,
,
«![]() »
»![]() ,
,
«![]() »
»![]() ,
,
«![]() »
»![]() ,
,
«![]() »
»![]() «
«![]() »
»![]() «
«![]() »
»![]() ,
,
«![]() »
»![]() «
«![]() »
»![]() «
«![]() »
»![]() ,
,
«![]() »
»![]() «
«![]() »
»![]() «
«![]() »
»![]() ,
,
«![]() »
»![]() «
«![]() ».
».
Универсальная учрф:
![]() «
«![]() »
»![]() ,
если
,
если
![]() не определено, то и
не определено, то и
![]() «
«![]() »
»![]() не определено.
не определено.
Функция
![]() реализуется универсальным вычислителем
с тем же алгоритмическим описанием, что
и одноименная функция в классической
теории чрф.
реализуется универсальным вычислителем
с тем же алгоритмическим описанием, что
и одноименная функция в классической
теории чрф.

Здесь
![]() - некоторые упрф. Тогда функция
- некоторые упрф. Тогда функция
![]() может быть описана как учрф:
может быть описана как учрф:
![]() ,
где
,
где
![]() ,
то есть
,
то есть
![]()
![]() .
.
Действительно,
![]() ,
где
,
где
![]() наименьшее
наименьшее
![]() ,
такое, что
,
такое, что
![]() .
.
1 Алонцо Черч (1903 г.р.) - один из наиболее выдающихся математиков ХХ века - специалистов в области оснований математики и математической логики.
