Языки сетей Петри.

Вернемся к рассмотрению способов задания семантики сетей Петри в форме множеств слов (формальных языков). Как правило, в качестве области интерпретации рассматривается класс рекурсивно-перечис-лимых множеств слов в алфавите . Известно несколько хорошо изученных вариантов определения языков сетей Петри, как способа определения их семантики. Денотат (семантическое значение) сетиобозначаетсяи определяется в зависимости от типазадания семантики. Полагая, что – конкатенация множеств слов, приведем несколько наиболее часто рассматриваемых в литературе типов семантики:

1. -типа – для определения языка сети Петри рассматриваются истории достижения маркировок из заданного конечного подмножества :

,

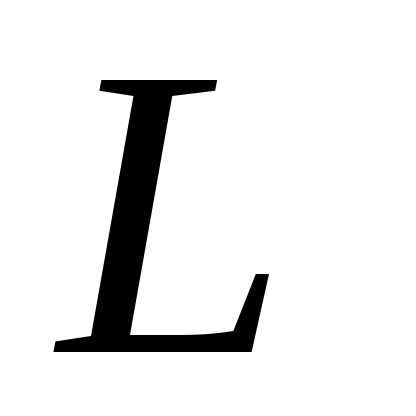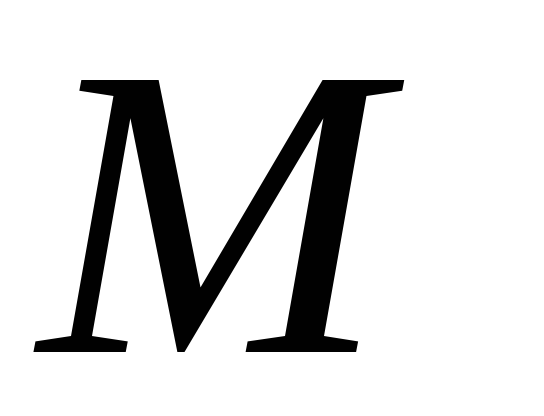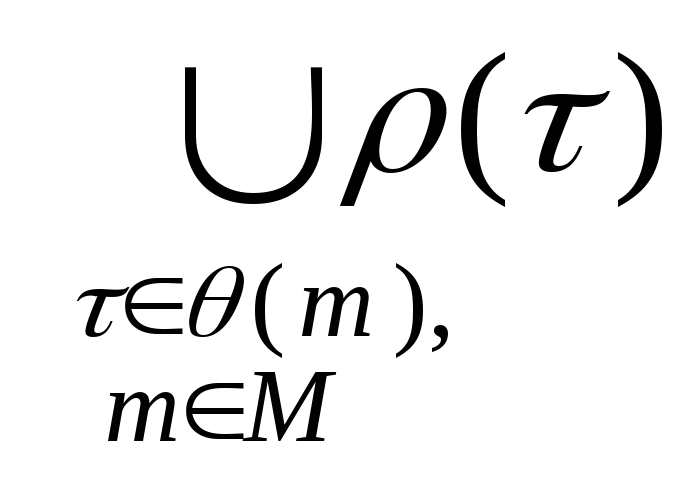2. -типа – для определения языка сети Петри рассматриваются истории достижения любых маркировок 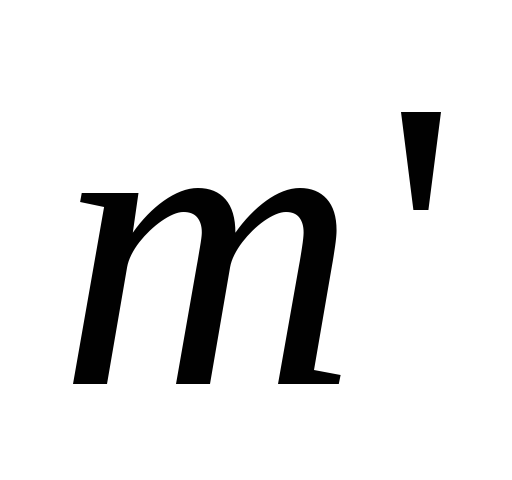, покрывающих любую из маркировок в заданном конечном подмножестве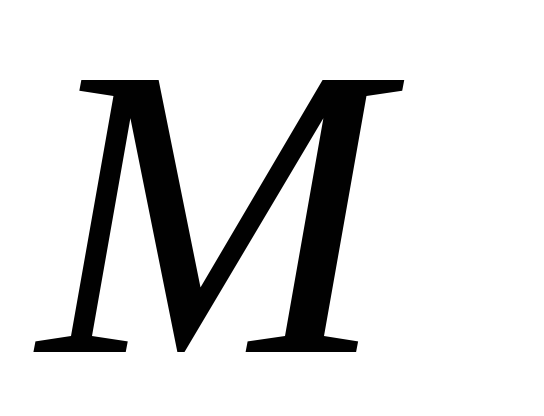(множество заключительных маркировок – ):

,

3. -типа – для определения языка сети Петри рассматриваются истории достижения любых тупиковых маркировок:

,

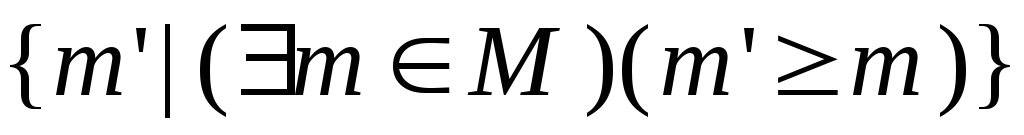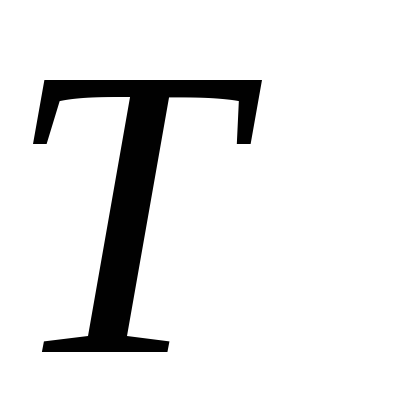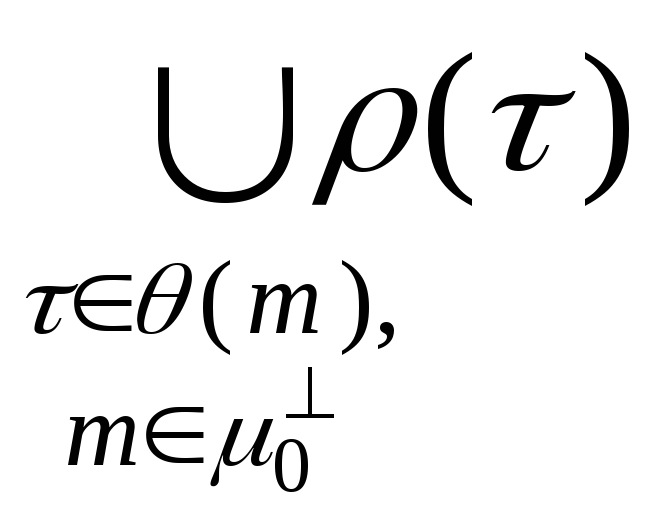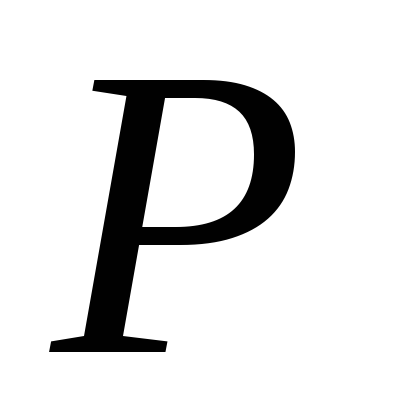4. -типа – для определения языка сети Петри рассматриваются истории достижения любых достижимых в сети маркировок (маркировок из ):

.

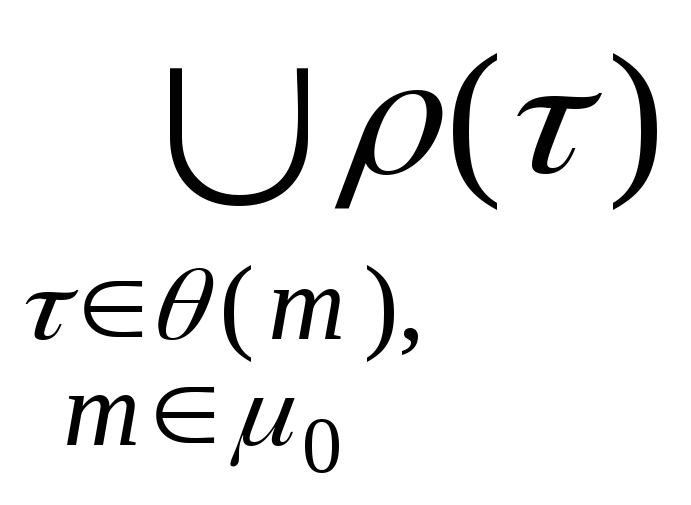В сочетании с тремя основными способами раскрашивания переходов в сети:

• свободного раскрашивания,

• произвольного раскрашивания (произвольными буквами из заданного алфавита),

• -раскрашивания (произвольными буквами из заданного алфавита или символом пустого слова ; в последнем случае переход иногда называют не окрашенным),

получается 12 основных классов формальных языков сетей Петри:

	-раскрашенные	Произвольно раскрашенные	Свободно раскрашенные
-типа
-типа
-типа
-типа

Известны следующие результаты о включениях этих классов языков:

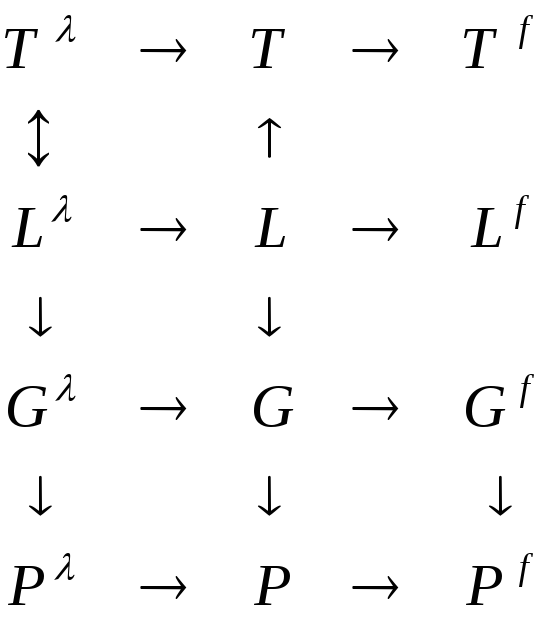
На рис. 7-9 приведены примеры сетей, реализующих некоторые языки -типа (с использованием произвольного и-раскрашивания переходов). На рис. 10 показано, как по сети, реализующей некоторый язык-типа с произвольным или-раскрашиванием переходов, построить реализующую этот же язык сетьс семантикой-типа и тем же способом раскрашивания переходов. При построении множество позиций остается неизменным, а каждому переходу в сетив сетисопоставляется подмножество переходов, окрашенных так же, как и исходный переход в сети. По построению очевидно, что для всякого слова, такого, что для сети , найдется историяповедения сети, такая, что она не приведет не приведет к получению «лишних» фишек (из разностимаркировок), т.е. для сетивыполняется, так как раскраска переходов в сетисохраняется и в сети. Верно также и обратное - если, то есть для сети , то найдется историяповедения сети, такая, что. Иными словами, на этом рисунке дана иллюстрация доказательства включенийи.

При анализе языков сетей Петри важную роль играет довольно очевидный результат. Пустьи- сети отличающиеся только своими начальными маркировкамии, причем такими, что, имеет место соотношение. Тогда очевидно, что если для некоторой последовательности переходовзначениеопределено, то иопределено, причем. Это свойство обычно называют семантической монотонностью сетей Петри. Отсюда, в частности следуют следующие утверждения относительно языков сетей Петри с любым способом раскрашивания переходов:

• ,

• ,

• .
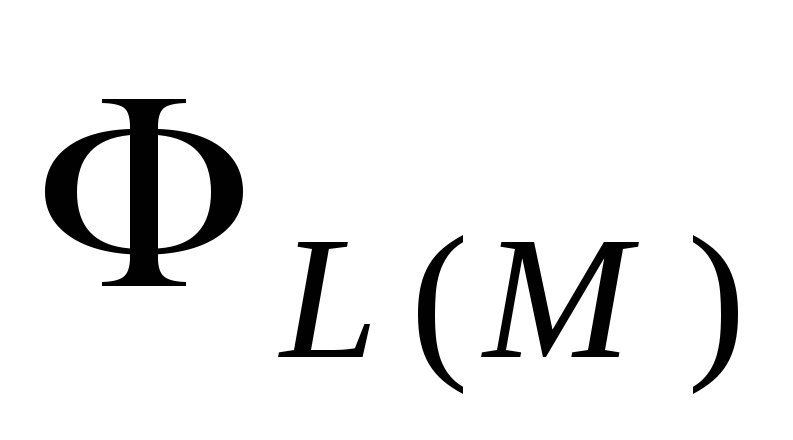
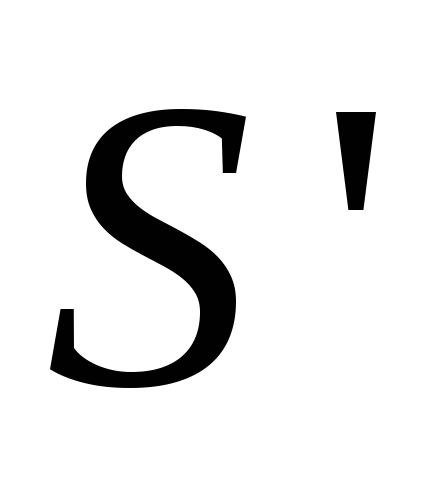
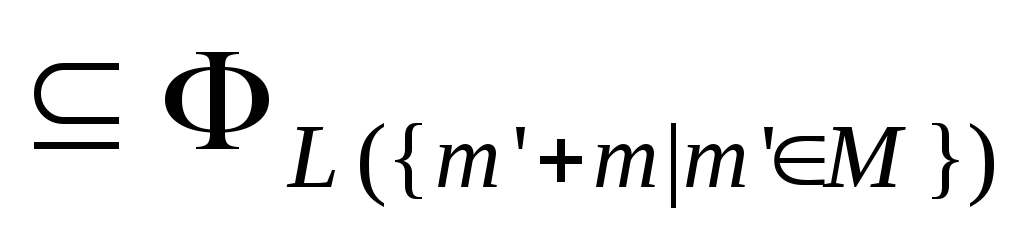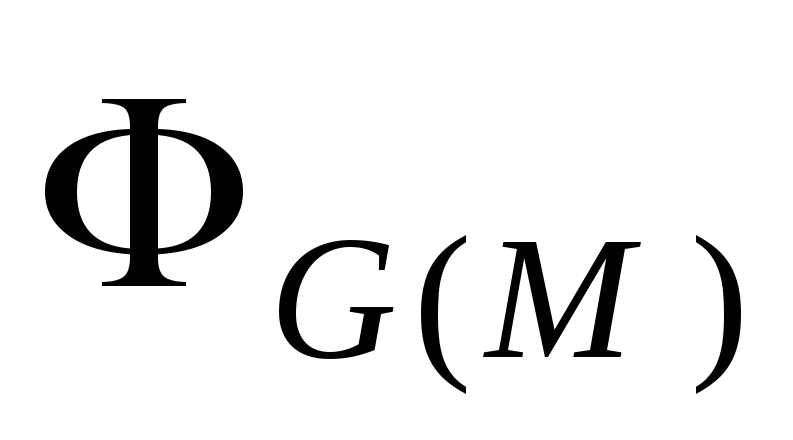
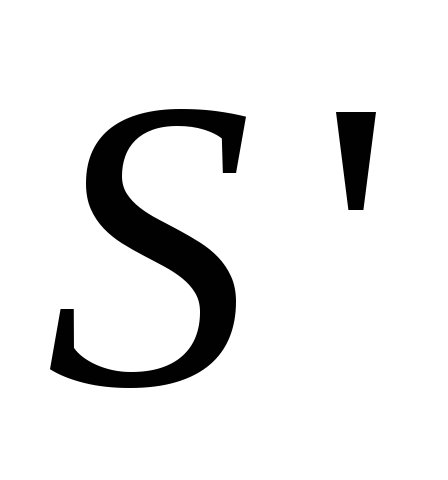
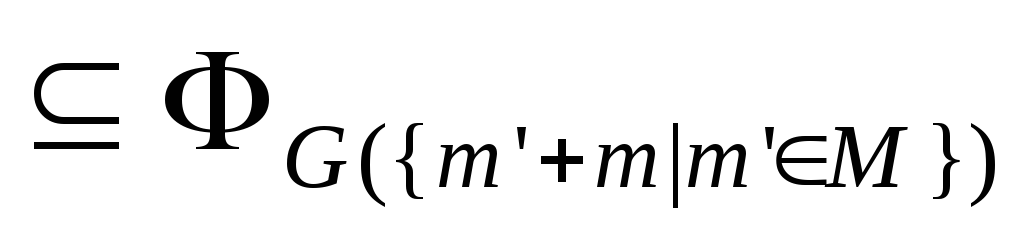
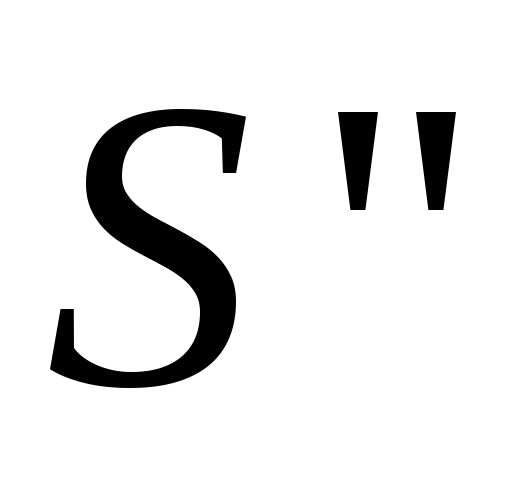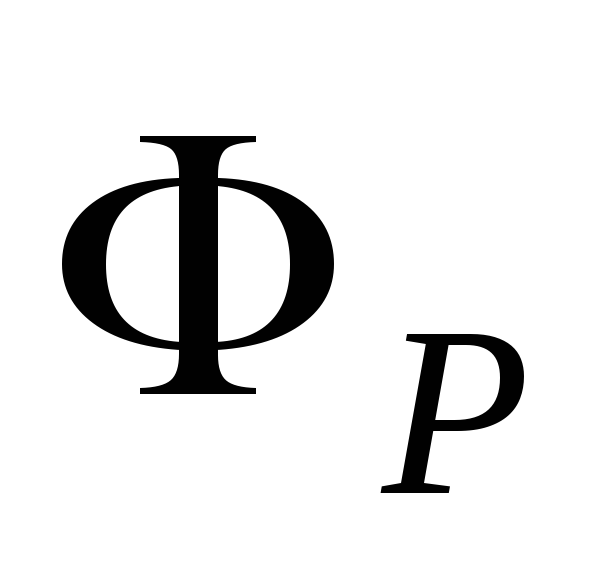
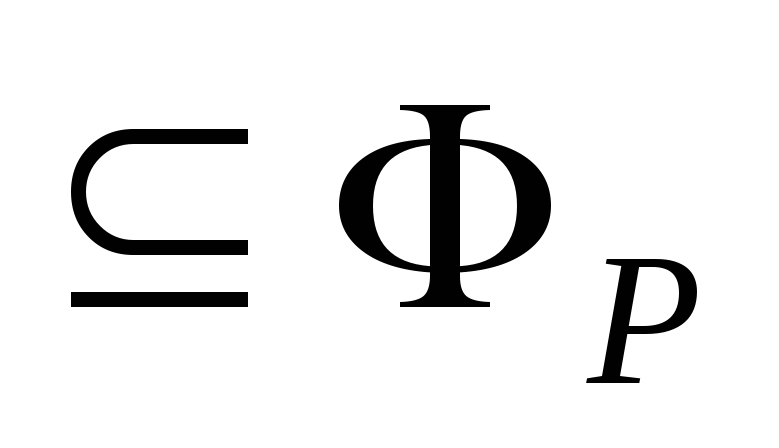