
- •Тема 5. Показатели вариации
- •1. Понятие вариации
- •2. Показатели вариации
- •2.1. Абсолютные и средние показатели вариации
- •2.2. Относительные показатели вариации
- •Анализ характера распределения в вариационных рядах
- •Понятие о закономерности распределения
- •Асимметрия распределения и эксцесс
- •Нормальное распределение
Асимметрия распределения и эксцесс
Выяснение
общего характера распределения
предполагает оценку степени его
однородности, а так же вычисление
показателей асимметрии и эксцесса.
Симметричным является распределение,
в котором частоты любых двух вариантов,
равноотстоящих в обе стороны от центра
распределения, равны между собой. Для
симметричных распределений средняя
арифметическая, мода, медиана совпадают
(т. е. равны). В связи с этим простейший
показатель асимметрии основан на
соотношении показателей центра
распределения: чем больше разница между
средними (![]() ),
тем больше асимметрия ряда. При этом,
если (
)
> 0 – асимметрия правосторонняя (правая
часть кривой длиннее). А если (
)
< 0 – асимметрия левосторонняя (левая
часть кривой длиннее).
),
тем больше асимметрия ряда. При этом,
если (
)
> 0 – асимметрия правосторонняя (правая
часть кривой длиннее). А если (
)
< 0 – асимметрия левосторонняя (левая
часть кривой длиннее).
Для
сравнительного анализа степени асимметрии
нескольких распределений рассчитывают
относительный показатель асимметрии
![]() :
:
![]()
Величина может быть положительной и отрицательной.

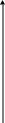 f
f
f
f
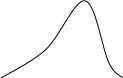 (х-мо)
> 0 (x-мe)
< 0
(х-мо)
> 0 (x-мe)
< 0



 As
>
0 As
<
0
As
>
0 As
<
0
 мо
< мe
<
мо
< мe
<
![]() мо
> мe
>
мо
> мe
>



![]()
![]() x
x
x
x
правосторонняя асимметрия левосторонняя асимметрия
Для симметричных распределений рассчитывается показатель эксцесса (островершинности). Наиболее точным является показатель, основанный на использовании центрального момента четвертого порядка:
![]()
![]()
 f f
f f
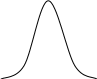
 f Ex > 0 Ex < 0
f Ex > 0 Ex < 0


 2
2
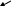 1
1

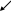 1
1
 3
3

 x
x
x
x
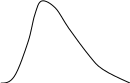
1. Нормальное распределение
2. Островершинное распределение
3. Плосковершинное распределение
Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения. В нормальном распределении Ех = 0.
Оценка показателей асимметрии и эксцесса позволяет сделать вывод о том, можно ли отнести данное эмпирическое распределение к типу кривых нормального распределения.
Нормальное распределение
Если распределение описывается кривой
![]() ,
,![]()
где
t
– нормированное отклонение, равное
![]() ,
,
то такое распределение называется нормальным. Нормальное распределение графически представляется в виде симметричной колоколообразной кривой. Нормальная кривая является идеализированной формой распределения, однако многие распределения приблизительно соответствуют нормальным.
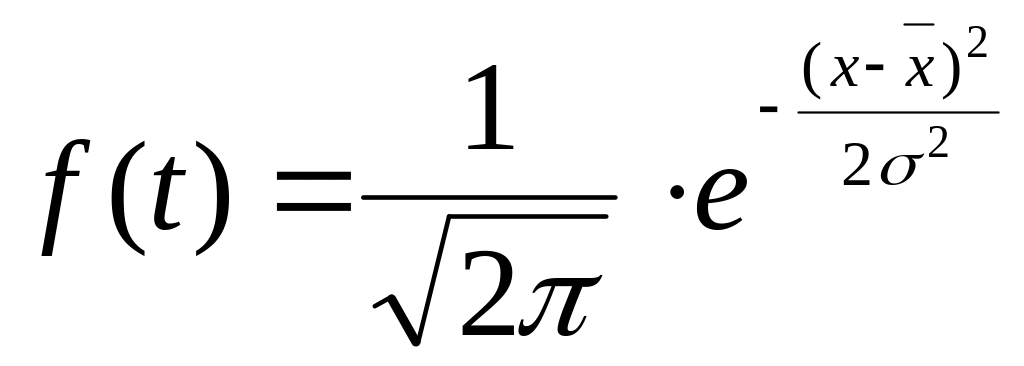
Таким образом, для построения нормальной кривой надо знать два параметра: и .
Е сли
не меняется, но растет величина ,
распределение носит более плосковершинный
характер.
сли
не меняется, но растет величина ,
распределение носит более плосковершинный
характер.
f

 3 1
< 2
< 3
3 1
< 2
< 3
 –
const
–
const

 2
2
 1
1

x
Если не меняется , а увеличивается , в этом случае кривая, не меняя своей формы, сдвигается вправо вдоль оси абсцисс:
f =const
=const
![]() <
<![]() <
<![]()
точка перегиба
x
![]()
Особенности кривой нормального распределения:
1.
Кривая симметрична относительно
максимальной ординаты. Максимальная
ордината соответствует значению
=
Мо
= Ме,
ее величина равна
![]() .
.
2. Кривая асимптотически приближается к оси абсцисс, продолжаясь в обе стороны до бесконечности. Следовательно, чем больше значения отклоняются от , тем реже они встречаются.
3.
Кривая имеет две точки перегиба,
находящиеся на расстоянии
![]() от
(см.
рис. выше)
от
(см.
рис. выше)
4. В промежутке
![]() находится 68,3% всех значений признака.
В промежутке
находится 68,3% всех значений признака.
В промежутке
![]() находится 95,4% всех значений признака.
В промежутке
находится 95,4% всех значений признака.
В промежутке
![]() находится 99,7% всех значений признака.
находится 99,7% всех значений признака.
Нормальное распределение возможно в том случае, когда на величину признака влияет большое число случайных причин. Действие этих причин независимо, и ни одна из них не имеет преобладающего влияния над другими. Для удобства вычислений величину t, зависящую от и , табулируют (таблица значений функции f(t)).
