3. Структурные средние величины.

В отличие от степенных средних, которые в значительной мере являются абстрактной характеристикой совокупности, структурные средние выступают как конкретные величины, совпадающие с вполне определенными вариантами совокупности. Это делает их незаменимыми при решении ряда практических задач. К таким показателям относится мода и медиана.

3.1 Мода.

Модой (М0) статистике называется величина признака (варианты), которая чаще всего встречается в данной совокупности.

Мода широко используется в коммерческой практике, при изучении покупательского спроса, регистрации цен. Мода применяется при экспертных оценках, при определе­нии наиболее ходовых размеров обуви, одежды, что учитывается при планировании их производства.

В дискретном ряду распределения мода – это варианта с наибольшей частотой.

Пример 6. Распределение покупательского спроса по размеру обуви.

Размер обуви	Число купленных пар	Накопленная численность
34	2	2
35	10	12
36	20	32
37	88 (мах)	120
38	19	139
39	9	148
40	1	149
ИТОГО:	149	-

По проведенным данным наибольшим спросом обуви пользуется размер 37. Т. е. В данном примере модой будет размер обуви 37.

М_о = 37

В интервальном вариационном ряду модой приближенно считают центральный вариант так называемого модального интервала, т. е. того интервала, который имеет наибольшую частоту (частость). В пределах интервала надо найти то значение признака, которое является модой. Конкретное значение моды для интервального ряда определяется формулой:

,

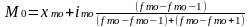где х_мо - нижняя граница модального интервала;

i_мo - величина модального интервала;

f_мо - частота, соответствующая модальному интервалу;

f_мо-1- частота, предшествующая модальному интервалу;

f_мо+1-частота интервала, следующего за модальным.

Пример 7. Распределение работников предприятия по стажу

Стаж (лет)	Число работников	Накопительная численность
До 2 2 - 4 4 - 6 6 - 8 8 - 10 свыше 10	4 23 20 35 (max) 11 7	4 27 47 82 93 100
Итого	100	-

Модальный интервал величины стажа работников: (6 – 8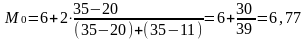) лет.

лет

3.2 Медиана.

Медиана (М_е) – это величина, которая делит численность упорядоченного вариационного ряда на две равные части: одна часть имеет значение варьирующего признака меньше, чем средний вариант, а другая – больше.

Что бы найти медиану в дискретном вариационном ряду, нужно сумму частот разделить пополам (и к полученному результату добавить ½, если сумма частот – нечетная величина). Медианой будет являться то значение признака, где накопленная (кумулятивная) частота составляет половину или больше половины всей суммы частот, а предыдущая накопленная частота меньше половины численности совокупности.

Так в примере 6:

То есть 75-я варианта делит упорядоченный ряд пополам. Для того, чтобы выяснить, каково значение 75-ой варианты, необходимо посчитать накопленную численность. В нашем примере 75-я варианта соответствует четвертому значению варьирующего признака и медианой будет размер обуви 37. Мода и медиана в данном примере совпали, но это происходит не всегда.

Для нахождения медианы в интервальном ряду сначала необходимо определить интервал, в котором она находится (медианный интервал). Медианным будет такой интервал, где накопленная (кумулятивная) частота составляет половину или больше половины всей суммы частот, а предыдущая накопленная частота меньше половины численности совокупности.

Формула медианы в интервальном ряду распределения имеет следующий вид:

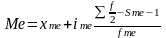
где х_ме - нижняя граница медианного интервала;

i_ме - величина медианного интервала;

f - сумма частот ряда;

S_ме-1 - сумма накопленных частот, предшествующих медианному интервалу;

f_ме - частота медианного интервала.

Найдем медиану для примера 7.

Сначала найдем медианный интервал:

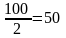
Медианный интервал – стаж работы (6 – 8) лет.

лет

Таким образом, ровно половина рабочих на предприятии имеют стаж работы меньше 6,17 лет.

Медиана используется при статистическом контроле качества продукции и технологическо­го процесса на промышленных предприятиях; при изучении рас­пределения семей по величине дохода и др.

Мода и медиана име­ют преимущество перед средней арифметической для ряда рас­пределения с открытыми интервалами.