2.5. Обработка результатов косвенных измерений
При косвенных измерениях искомая
величина
является функцией ряда других величин
- аргументов
.
.
(2.38)
Результат косвенных измерений оценивается
погрешностью
,
которая определяется погрешностями
аргументов
,
где
,
и наличием статистической связи
(корреляции) между аргументами.
Представим погрешности аргументов
в виде систематической
и случайной
составляющих
. (2.39)
Тогда результат косвенных измерений можно представить через погрешности аргументов
.
(2.40)
Разложим функцию
в ряд Тейлора, отбросим отклонения выше
первого порядка и выразим результат
через среднеарифметические значения
и погрешности аргументов
, (2.41)
где
-
коэффициент влияния i –
го аргумента;
- частная погрешность i –
го аргумента.
Из формулы (2.41) получаем выражение для оценки результата косвенного измерения
,
(2.42)
а также выражения для оценки систематической
и случайной
погрешностей результата косвенного
измерения
;
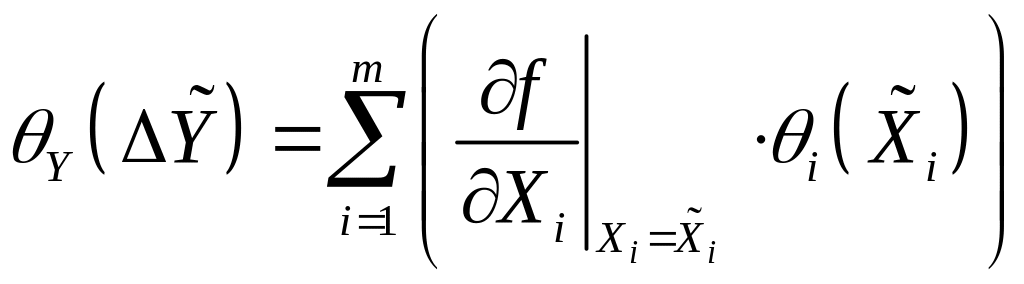(2.43)
.
(2.44)
Из выражения (2.44) можно найти приближенное
выражение для оценки среднеквадратического
отклонения
случайной погрешности результата
косвенного измерения в зависимости от
оценок среднеквадратических отклонений
случайных погрешностей аргументов
,
(2.45)
где
- оценка коэффициента корреляции,
определяющая меру статистической связи
случайных величин
и
.
Все возможные оценки коэффициента
корреляции
лежат в интервале от -1 до +1. Установить
значение
обычно затруднено, поэтому рассматривают
два случая:
(отсутствие статистической связи) и
(полная статистическая связь).
При формула (2.45) преобразуется к виду
,
(2.46)
т.е. оценки среднеквадратических отклонений случайных погрешностей аргументов суммируются геометрически как независимые случайные.
При формула (2.45) преобразуется к виду
,
(2.47)
т.е. оценки среднеквадратических отклонений случайных погрешностей аргументов суммируются алгебраически с учетом знаков.
Результат косвенных измерений записывается в соответствии с выражением (2.24), т.е. также как и при прямых измерениях, но доверительный интервал вычисляется с учетом оценок среднеквадратических отклонений случайных погрешностей аргументов и оценок коэффициентов корреляции между ними.
2.6. Обработка результатов совместных измерений
В практике измерений часто возникает необходимость в экспериментальном определении зависимости между двумя или большим числом измеряемых физических величин. Предположим, что между физическими величинами x и y имеет место аналитическая зависимость, которую представим выражением
,
(2.48)
где
- неизвестные коэффициенты,
.
В результате измерений можно получить
n экспериментальных
точек с координатами
на координатной плоскости XOY,
причем
.
По расположению экспериментальных
точек на координатной плоскости можно
сделать предположение о виде
аппроксимирующей функции. Ее можно
представить какой-либо конкретной
функцией, например, синус, тангенс,
логарифм, экспонента, арктангенс и др.
или полиномом высокой степени. В общем
виде аппроксимирующую функцию представим
в виде
, (2.48)
где
искомые коэффициенты аппроксимирующей
функции,
.
Необходимо определить коэффициенты , используя результаты измерений, выполненные с некоторой погрешностью. Будем считать, что погрешность измерений носит случайный характер и подчиняется нормальному закону распределения плотности вероятности случайных погрешностей. Для решения подобных задач наибольшее распространение получил метод наименьших квадратов.
Погрешности измерения, а также неточный
выбор аппроксимирующей функции являются
причиной возникновения погрешности
между вычисленным значением функции
по измеренному значению аргумента
и измеренным значением функции
.
(2.49)
В соответствии с методом наименьших
квадратов аналитическая зависимость
будет наилучшим образом описывать
экспериментальную, если сумма квадратов
погрешности
будет минимальна.
. (2.50)
Для вычисления
неизвестных коэффициентов
необходимо записать систему
уравнений
. (2.51)
Или после преобразований в развернутом виде
(2.52)
Приведенная система уравнений достаточно просто решается в системе MathCad. Средствами MathCad может быть организована и вся процедура вычисления коэффициентов аппроксимирующей функции по методу наименьших квадратов.