2.3 Передаточные функции внутреннего оптимального замкнутого и разомкнутого контуров сар

Передаточная функция разомкнутой САР будет иметь следующий вид:

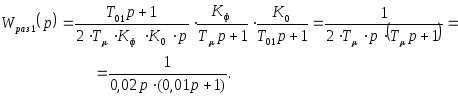
Тогда передаточная функция замкнутой системы с единичной отрицательной обратной связью будет определяться следующим выражением:

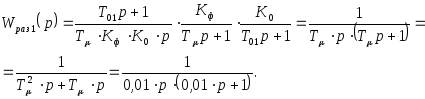
Тогда передаточная функция замкнутой системы с единичной связью будет определяться следующим образом:

Тогда передаточная функция замкнутой системы с единичной отрицательной обратной связью определится следующим образом:

Определение передаточной функции разомкнутой и замкнутой САР при изменении значения постоянной времени

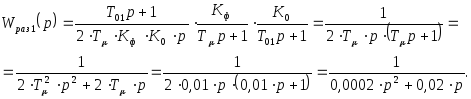
Тогда передаточная функция замкнутой САР при единичной отрицательной обратной связи равно будет определяться следующим выражением:

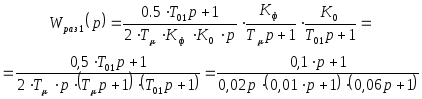
Тогда передаточная функция замкнутой САР будет определяться следующим выражением:

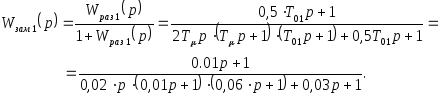
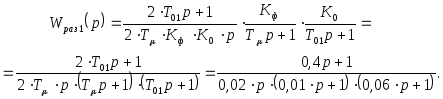
Аналогично двум другим случаям, передаточная функция замкнутого контура САР определится следующим выражением:

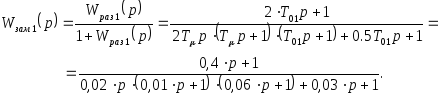
2.4 Аналитический расчёт графиков переходных процессов оптимального внутреннего замкнутого контура

Полученное выражение свидетельствует о соответствии передаточной функций разомкнутого и замкнутого контуров оптимальной САР второго порядка, другими словами внутренний контр оптимизирован по модульному оптимуму. Поэтому переходная функция станет оптимальной и будет определяться выражением:

(10)

Переходные функции оптимальной САР зависят от порядка и номера контура регулирования ОР

В данном случае

Характеристическое уравнение

; (11)

или , где

Корни характеристического уравнения

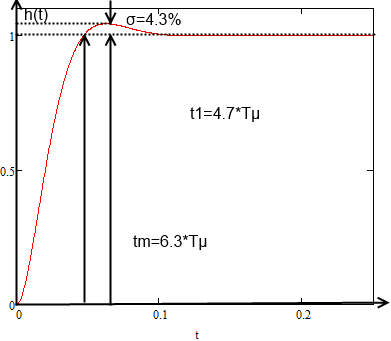
Рис. 5 Кривая переходного процесса по модульному оптимуму

Переходная функция характеризуется следующими показателями

Перерегулирование

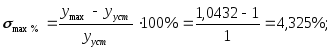
Время первого достижения установившегося значения .

Время первого достижения максимального значения .

Время переходного процесса (вхождения в 2-х процентную зону)

Таким образом, передаточные функции разомкнутого и замкнутого контуров соответствуют оптимальной системе второго порядка, т.е. внутренний контур регулирования двухконтурной САР оптимизирован по модульному оптимуму. Поэтому переходная функция станет оптимальной и будет определяться выражением (10). Такая переходная функция представлена на рис.5.

Параметры переходного процесса также оптимальны. Они получены при оптимальной настройке регулятора, при которой

где постоянная времени обратной связи регулятора

постоянная времени интегрирования регулятора

оптимальное значение коэффициента, определяющего соотношение постоянных времени замкнутого контура.

На динамические показатели замкнутого внутреннего контура оказывает влияние действительная настройка регулятора, а именно, выбор значений постоянных времени регулятора и . Динамически показатели САР в этом случае могут быть оценены по частотным методам оценки качества САР. Для этого необходимо построить логарифмические амплитудную и фазовую частотные характеристики САР с использованием передаточных функций разомкнутой и замкнутой САР.

Наиболее точно динамические показатели могут быть определены путём расчёта переходных процессов по методу структурного моделирования на ЭВМ. При этом желательно исследовать следующие варианты настройки параметров регулятора:

а) изменение постоянной времени интегрирования регулятора:

1) базовый вариант оптимальной настройки;

2)

3)

б) изменение постоянной времени обратной связи регулятора:

1) базовый вариант оптимальной настройки;

2)

3)

Для построения переходных процессов можно воспользоваться приложением MATLAB Simulink, для этого на рис.6 приведём схему для построения соответствующих кривых переходных процессов.

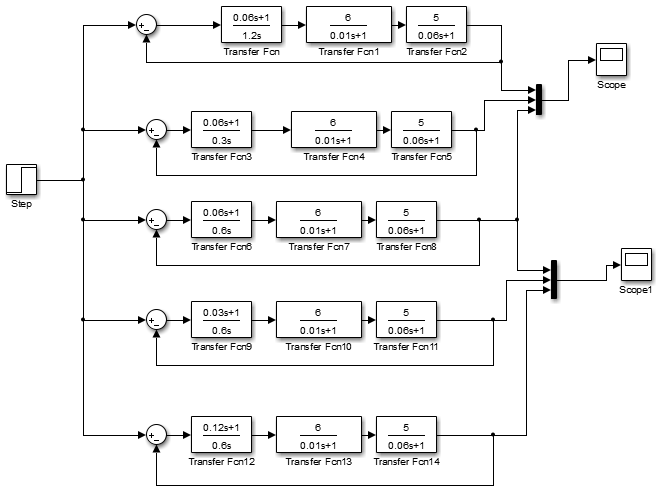
Рис. 6 Схема ОР для исследования кривых переходных процессов

а)

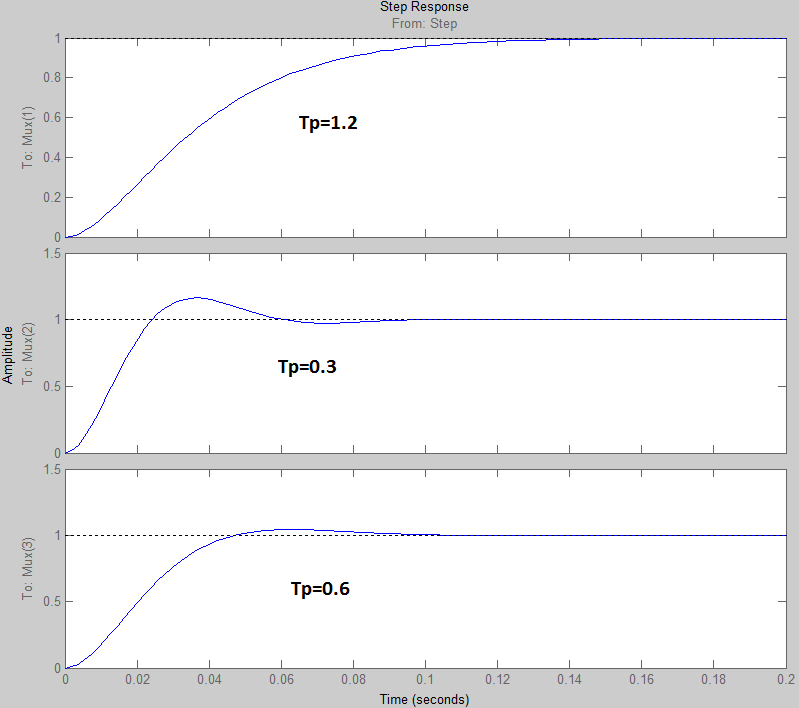
б)

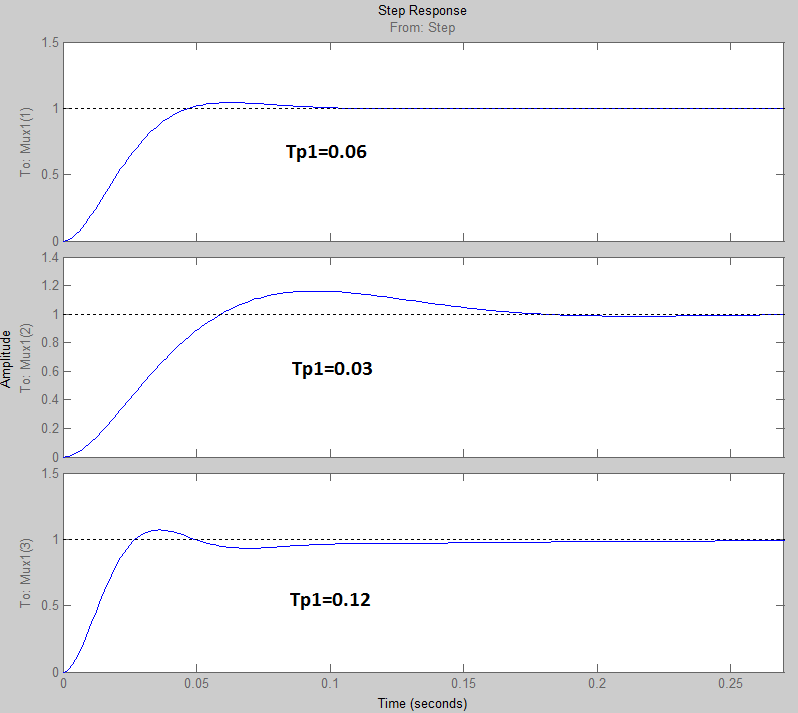
Рис. 6 Кривые переходных процессов:

а) - при изменении б) - при изменении

а)

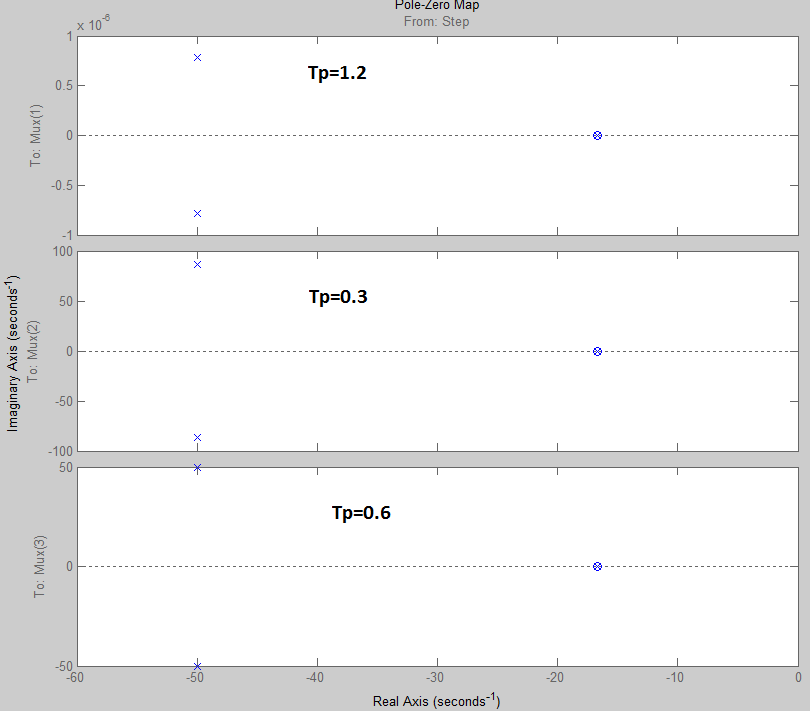
б)

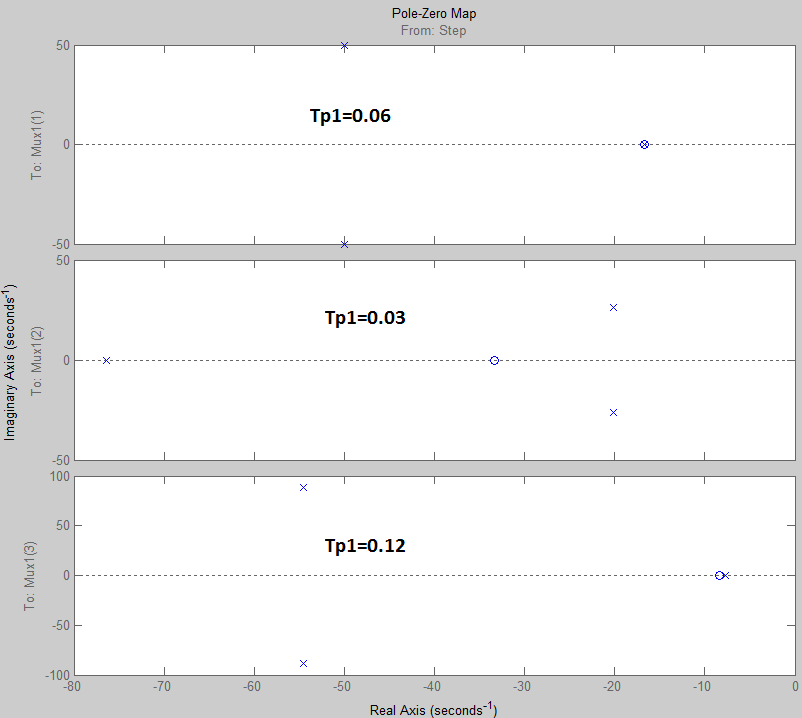
Рис. 7 Распределение нулей и полюсов

а) - при изменении б) - при изменении

Вывод: Итак, анализируя переходные процессы, представленные на рис.6 а, б можно установить, что:

1) При изменении :

1.1) При уменьшении постоянной времени (коэффициента а, а значит значения ) снижается время переходного процесса (другими словами, увеличивается быстродействие), но возрастает перерегулирование

1.2) При снижении постоянной времени , наоборот снижается перерегулирование, но снижается быстродействие (время переходного процесса увеличивается).

2) При изменении

2.1) При уменьшении постоянной времени обратной связи происходит увеличение и уменьшению (т.е. увеличение быстродействия)

2.2) При увеличении также происходит увеличение , но в большей степени по отношению к оптимальной настройке, однако происходит увеличение (т.е. снижение быстродействия).

Теперь можно сделать вывод, что любое отклонение от оптимальной настройки (т.е. изменение либо постоянной времени , либо постоянной времени обратной связи ) приводит либо к увеличению перерегулирования , либо увеличению времени переходного процесса (снижению быстродействия). Поэтому напрашивается вывод о том, что оптимальные настройки являются наиболее благоприятными для переходного процесса и облегчают процесс регулирования объектом.