8. Побудова лінії перетину площин

Рис. 8 Рис. 9

   

На рис. 8 задані дві площини Σ і Ρ з різним ухилом: ухил площині Σ більше, тому інтервали менше, а ухил Ρ менше, тому інтервал більше. Дві площини перетинаються по прямій лінії. Для її побудови досить побудувати дві точки. Такими точками будуть точки перетину однойменних горизонталей, тому перетинатися можуть тільки ті прямі, які лежать в одній площині. Горизонталі, що мають позначку 7, лежать в одній горизонтальній площині, а значить перетинаються (т. М ). Аналогічно будується точка N . Поєднавши дві точки, що належать обом площинам, отримаємо проекцію лінії перетину.

На рис.9 задані дві площини Φ і Λ, що мають однаковий ухил, тому інтервали їх рівні, тому лінія перетину цих площин буде бісекторною (M N ). Будується вона так само, як у попередньому прикладі.

9. Задання прямого кругового конуса

У проекціях з числовими відмітками форма будь-яких поверхонь досить повно характеризується їх горизонталями. Всі способи є різновидом каркасного способу задання поверхонь. Для виконання графічної роботи достатньо знати, як задається прямий круговий конус і топографічна поверхня.

Якщо прямий круговий конус перетнути поруч паралельних площин, розташованих перпендикулярно осі обертання, то вони перетнуть його по концентричних колах-горизонталях. (Рис.10). Якщо відстані між площинами рівні одній одиниці, то відстані між колами на плані будуть рівні інтервалу.

Таким чином, на кресленні прямий круговий конус задається проекцією, що утворює з нанесеними інтервалами (проградуйована проекція твірної), через які можна провести кругові горизонталі, (рис.11).

Рис. 10 Рис. 11

10. Побудова лінії перетину конічної поверхні з площиною.

Конічна поверхня з площиною перетинається по плоскій кривій лінії, яка будується по точках перетину горизонталей площини з горизонталями конуса з такою ж відміткою, тому лежать в одній горизонтальній площині. (Рис.12). Отримані точки з'єднуються плавною кривою лінією.(M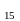 N ).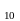

 

Рис. 12 Рис. 13

На рис.12 прямий круговий конус розташований вершиною вгору, тому кожна наступна горизонталь на одну позначку нижче, ніж попередня. У площині точно так само.

На рис. 13 конічна поверхня розташована вершиною вниз і площина дотична до неї. Кожна наступна горизонталь на одну позначку вище попередньої.

Лінію дотику площині виділяти не потрібно, вона залишається тонкою суцільною лінією(M N )

11. Побудова горизонталей на укосах дороги

На відкосах від майданчика горизонталі паралельні краям майданчика, тому-що вони теж є горизонталями. (Рис.9), а всі горизонталі паралельні між собою.

Відкіс від дороги – це площина, дотична до системи конусів, що стоять уздовж бардюри (краю) дороги і розташованих в точках перетину горизонталей дороги з бардюрою дороги або кордоном канавки. Дорога має ухил, а тому горизонталі відкосів від неї не будуть паралельні її краям. Конуси, розташовані вздовж кромки дороги, можуть бути вершинами вгору або вниз.

Рис. 14

На рис 14 зображена площина Σ дотична до сімейства конусів, вершини яких розташовані вгору з одним і тим же нахилом, що утворюють осі обертання. Горизонталь – окружність конуса, розташована на одну позначку нижче ніж вершина, і вершина наступного конуса, розташовані на позначку нижче тому, мають однакову позначку. Тому пряма, проведена через вершину наступного конуса і дотична до горизонталі – окружності попереднього конуса є горизонталь площини Σ.

Решта горизонталі площини Σ будуть паралельні їй.

На рис. 15 показується як будуються на кресленні горизонталі площини, дотичної до конусам. Масштаб ухилу її проводиться на будь-якому з конусів

Рис. 15

Для спрощення побудови досить побудувати:

а) одну горизонталь. б) масштаб падіння, перпендикулярний їй, з нанесеними інтервалами. в) горизонталі площини, проведені через інтервали і паралельні побудованої горизонталі.

 

Рис. 16

На рис 16 зображена площина Σ дотична до сімейства конусів, вершини яких розташовані вниз і знаходяться в точках перетину горизонталей дороги з її межею. Всі конуси з однаковим нахилом, що утворюють до осей обертання. Вершина кожного наступного конуса на одну позначку більше. Так як горизонталь – окружність попереднього конуса і вершина наступного конуса мають одну і ту ж позначку, то дотична, проведена через вершину конуса до кола - горизонталі, і буде горизонталлю площини Σ.

Рис. 17

На рис. 17 показано, як будуються горизонталі площини Σ на кресленні. Масштаб ухилу площини укосу проводиться з вершини будь-якого конуса перпендикулярно горизонталям (через точки дотику горизонталей площині з горизонталями конуса).