О твет: 0 1 2 3 4

0,6561 0,2916 0,0486 0,0036 0,0001

23. Охотник, имеющий 4 патрона, стреляет в цель до первого попадания или пока не израсходует все патроны. Найти математическое ожидание и дисперсию числа израсходованных патронов, если вероятность попадания при каждом выстреле равна 0,25.

Ответ: 2,734; 1,57.

24. Прядильщица обслуживает 1000 веретен. Вероятность обрыва нити на одном веретене в течение одной минуты равна 0,003. Найти вероятность того, что в течение одной минуты произойдет ровно два обрыва, менее двух обрывов, более двух обрывов, хотя бы один обрыв.

Ответ: 0,224; 0,1991; 0,5769; 0,95.

25. Найти закон распределения и функцию распределения числа попаданий в корзину мячом при одном броске, если вероятность попадания при каждом броске равна Р.

Ответ:

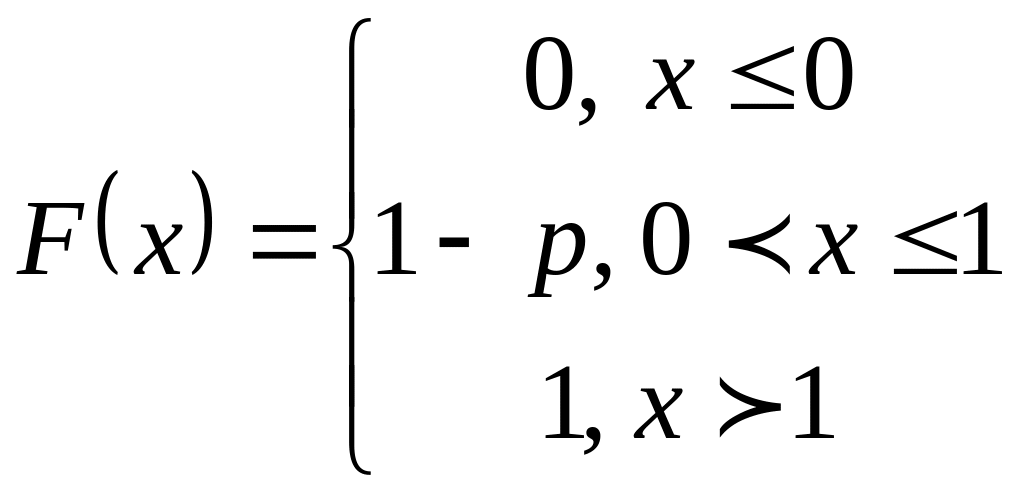
Ответ: 2,996.

З А Д А Н И Е 6

Непрерывные случайные величины

Контрольные вопросы

1. Какая случайная величина называется непрерывной?

2. Что называется функцией распределения?

3. Что называется плотностью вероятности?

4. Какова связь между функцией распределения и плотностью вероятности?

5. Приведите формулы для вычисления математического ожидания и дисперсии непрерывной случайной величины.

26.Функция распределения случайной величины X имеет вид

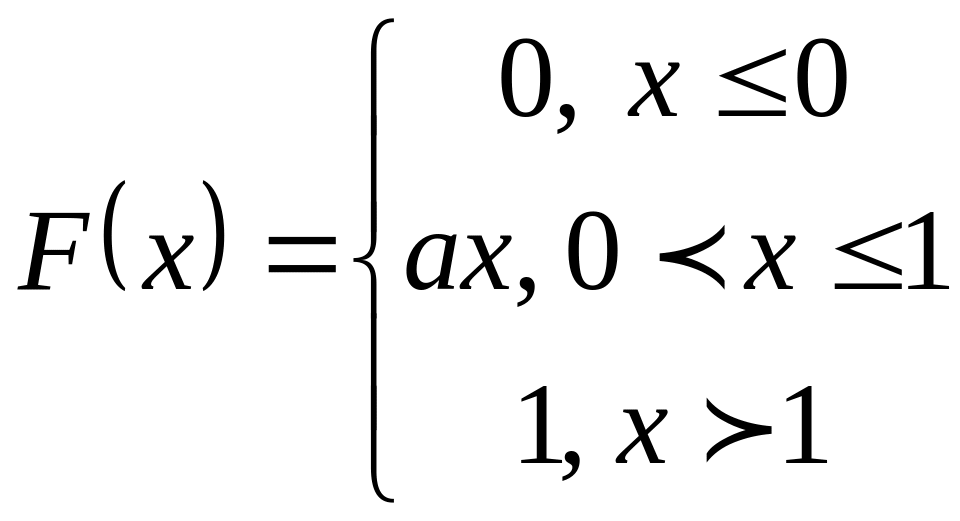
Найти , плотность вероятности, вероятность того, что значение случайной величины попало в интервал от 0,25 до 1,5, математическое ожидание и среднее квадратическое отклонение.

Ответ: =1; M(X) = 0,5; (X) = 0,29; P(0,25‹X‹1,5) =0,75

27. График плотности вероятности случайной величины Х изображен на рисунке ( 0). Написать выражение для плотности распределения, вычислить математическое ожидание, дисперсию, среднее квадратическое отклонение и вероятность попадания в интервал

 Ответ:

1/

M(X) = D(X)= (X)=

- 

P

28. Автобус некоторого маршрута идет строго по расписанию с интервалом 5 мин. Найти вероятность того, что пассажир, подошедший к остановке, будет ожидать автобус не более 3 мин.

Ответ: 0,6.

29. Плотность вероятности случайной амплитуды боковой качки корабля определяется формулой (закон Релея):

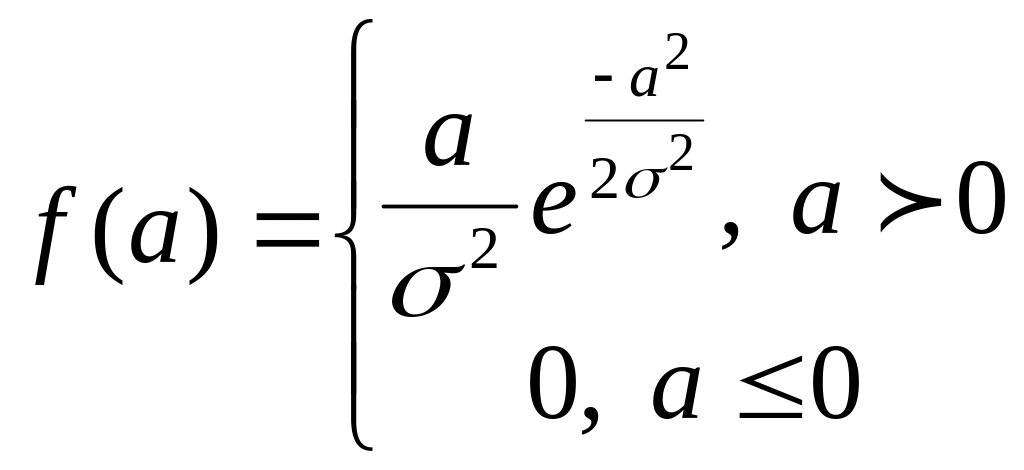
где ² – дисперсия угла крена. Одинаково ли часто встречаются амплитуды меньше и больше средней?

Ответ:

30. Найти математическое ожидание и дисперсию случайной величины Х, подчиненной закону распределения Лапласа

Ответ: 0; 2.

З А Д А Н И Е 7

Нормальный закон распределения и системы случайных величин

Контрольные вопросы

1. Что такое нормальный закон распределения?

2. Чем вызван почти универсальный характер нормального распределения?

3. Что такое коэффициент корреляции? Что он характеризует?

4. Какова связь между некоррелированностью и независимостью?

31.Случайная величина Х распределена нормально с параметрами =10 и =2. Найти вероятность того, что значение случайной величины Х попадет в интервал (12: 14)

Ответ: 0,1359.

32Случайные ошибки измерения подчинены нормальному закону с параметрами =0 и =20 мм. Найти вероятность того, что при трех независимых измерениях ошибка хотя бы одного из них не превзойдет по абсолютной величине 4 мм.

Ответ: 0,4.

33Случайная величина Х распределена нормально с параметрами =10 и =5. Найти интервал, в который с вероятностью 0,9973 попадет значение Х в результате опыта.

Ответ: (-5; 25).

34Бомбардировщик пролетает вдоль места длиною 30 и шириною 8 м. Случайные величины Х и У – расстояние от места разрыва бомбы до осей симметрии моста – независимы и подчинены нормальному закону распределения с математическими ожиданиями, равными нулю и средними квадратическими отклонениями, равными соответственно 6 и 4 м. Найти вероятность попадания при одной сброшенной бомбе и вероятность хотя бы одного попадания при двух бомбах.

Ответ: 0,674; 0,894.

35.Дана система случайных величин Х и У. Найти безусловные и условные математические ожидания и дисперсию компонент Х и У, а также коэффициент корреляции

Х У	2	-1	3
0,1	0,25	0,05	0,10
0,2	0,45	0,10	0,05

Ответ: М(Х) = 1,7; D(Х) ==1,41; М(Y) = 0,16; D(Y) == 0,028;

М(ХY = 0, 1) = 158; М(ХY = 0, 2) = 1912;

М(YХ = 2) = 23140; М(YХ = -1) =1/6;

М(Y/Х = 3) == 2/15;