
Методички / Numeration
.docФальк В.Н.
Нумерация рекурсивных множеств
конструктивных объектов.
Нумерацией
элементов множества
![]() (или, короче, нумерацией множества
(или, короче, нумерацией множества
![]() )
назовем конструктивно определенное
взаимно-однозначное отображение
)
назовем конструктивно определенное
взаимно-однозначное отображение
![]() на множество
на множество
![]() всех натуральных чисел (для счетных
множеств) или на его подмножество
всех натуральных чисел (для счетных
множеств) или на его подмножество
![]() (для конечных множеств из
(для конечных множеств из
![]() элементов). Далее, как правило, будут
рассматриваться только счетные множества,
так как для конечных множеств теоретических
проблем не возникает. Очевидно, что если
для счетного множества существует хотя
бы одна нумерация, то существует
неограниченное количество различных
нумераций (счетное только в силу
требования их конструктивного
определения). Если рассматривается
некоторая конкретная нумерация или
выбор конкретной нумерации не имеет
принципиального значения, то далее
«
элементов). Далее, как правило, будут
рассматриваться только счетные множества,
так как для конечных множеств теоретических
проблем не возникает. Очевидно, что если
для счетного множества существует хотя
бы одна нумерация, то существует
неограниченное количество различных
нумераций (счетное только в силу
требования их конструктивного
определения). Если рассматривается
некоторая конкретная нумерация или
выбор конкретной нумерации не имеет
принципиального значения, то далее
«![]() »
»![]() обозначает номер элемента
обозначает номер элемента
![]() в нумерации элементов множества
в нумерации элементов множества
![]() .
Множество с некоторой конкретной
нумерацией будем называть нумерованным
множеством (понятие нумерованного
множества является аналогом понятия
именованного множества, введенного
В.Н. Редько, для бесконечных счетных
множеств).
.
Множество с некоторой конкретной
нумерацией будем называть нумерованным
множеством (понятие нумерованного
множества является аналогом понятия
именованного множества, введенного
В.Н. Редько, для бесконечных счетных
множеств).
Рассмотрим
некоторые приемы нумерации при
общепринятых способах определения
конструктивных множеств. Множество
![]() натуральных чисел нумерует само себя:
натуральное число есть его номер во
множестве натуральных чисел. Множество
натуральных чисел нумерует само себя:
натуральное число есть его номер во
множестве натуральных чисел. Множество
![]() ,
полученное включением в счетное множество
,
полученное включением в счетное множество
![]() нового элемента
нового элемента
![]() ,
будем обозначать
,
будем обозначать
![]() и нумеровать так: «
и нумеровать так: «![]() »
»![]() ,
для всех
,
для всех
![]() «
«![]() »
»![]() «
«![]() »
»![]()
![]() 1.
Используя эту нумерацию, легко определить
множество
1.
Используя эту нумерацию, легко определить
множество
![]() – свободное объединение нумерованного
счетного множества
– свободное объединение нумерованного
счетного множества
![]() и не пустого конечного множества
и не пустого конечного множества
![]() (
(![]() и
и
![]() не пересекаются,
не пересекаются,
![]() обозначается как
обозначается как
![]() ):
):
![]()
![]() и его нумерацию: если
и его нумерацию: если
![]() ,
то «
,
то «![]() »
»![]() «
«![]() »
»![]() ,
если
,
если
![]() ,
то «
,
то «![]() »
»![]() «
«![]() »
»![]()
![]() .
.
Введенная
выше нумерация множества, полученного
операцией включения нового элемента,
обладает свойством сохранения порядка
номеров элементов, которые они имели
место в исходном множестве
![]() .
Для возможности использования любой
обладающей этим свойством нумерации
множества, полученного включением в
бесконечное нумерованное множество
нового элемента, введем по определению
обобщенную операцию
.
Для возможности использования любой
обладающей этим свойством нумерации
множества, полученного включением в
бесконечное нумерованное множество
нового элемента, введем по определению
обобщенную операцию
![]() с натуральным параметром
с натуральным параметром
![]() (очевидно, что для всякого бесконечного
нумерованного множества
(очевидно, что для всякого бесконечного
нумерованного множества
![]() существуют такие
существуют такие
![]() и нумерованное множество
и нумерованное множество
![]() ,
что
,
что
![]() ,
причем «
,
причем «![]() »
»![]() ):
):
![]() .
.
Очевидно,
что «![]() »
»![]() ,
а для всех
,
а для всех
![]() «
«![]() »
»![]() «
«![]() »
»![]() ,
если «
,
если «![]() »
»![]() ,
и «
,
и «![]() »
»![]() «
«![]() »
»![]() ,
если «
,
если «![]() »
»![]() .
.
Множество
![]() – свободное объединение (
– свободное объединение (![]() )
двух бесконечных нумерованных множеств
)
двух бесконечных нумерованных множеств
![]() и
и
![]() определим как
определим как
![]()
![]() ,
откуда следует его нумерация: если
,
откуда следует его нумерация: если
![]() ,
то «
,
то «![]() »
»![]() «
«![]() »
»![]() ,
если
,
если
![]() ,
то «
,
то «![]() »
»![]() «
«![]() »
»![]() .
Определенная таким образом операция
свободного объединения двух бесконечных
нумерованных множеств тоже обладает
свойством сохранения порядка следования
элементов, имевшем место в объединяемых
множествах. Однако, это не единственный
способ определения с этим свойством.
Для общего случая можно ввести операцию
объединения, параметризованную
произвольной общерекурсивной унарной
функцией
.
Определенная таким образом операция
свободного объединения двух бесконечных
нумерованных множеств тоже обладает
свойством сохранения порядка следования
элементов, имевшем место в объединяемых
множествах. Однако, это не единственный
способ определения с этим свойством.
Для общего случая можно ввести операцию
объединения, параметризованную
произвольной общерекурсивной унарной
функцией
![]() .
Тогда
.
Тогда

Очевидно,
что рассмотренная ранее нумерация
свободного объединения двух бесконечных
нумерованных множеств является частным
случаем для
![]() ,
т.е.
,
т.е.
![]() для всех
для всех
![]() .
Если не использовать сведение к нумерации
свободного объединения двух счетных
нумерованных множеств, то можно определить
и нумерацию свободного объединения
.
Если не использовать сведение к нумерации
свободного объединения двух счетных
нумерованных множеств, то можно определить
и нумерацию свободного объединения
![]() конечного числа
конечного числа
![]() счетных множеств таким образом, что
если
счетных множеств таким образом, что
если
![]() ,
то «
,
то «![]() »
»![]()
![]() «
«![]() »
»![]() .
.
Действительно,
пусть
![]() ,
где
,
где
![]()
Особое
значение для практической нумерации
конструктивных множеств имеет нумерация
множества упорядоченных пар
![]() элементов
элементов
![]() и
и
![]() двух бесконечных нумерованных множеств
двух бесконечных нумерованных множеств
![]() и
и
![]() ,
т.е. элементов их декартова произведения
,
т.е. элементов их декартова произведения

![]() .
Известно несколько удобных способов
нумерации декартова произведения,
удовлетворяющих требованию монотонности
нумерации: «
.
Известно несколько удобных способов
нумерации декартова произведения,
удовлетворяющих требованию монотонности
нумерации: «![]() »
»![]() «
«![]() »
»![]() ,
если «
,
если «![]() »
»![]() «
«![]() »
»![]() ,
и
«
,
и
«![]() »
»![]() «
«![]() »
»![]() ,
если «
,
если «![]() »
»![]() «
«![]() »
»![]() .
Опишем основные из них.
.
Опишем основные из них.
-
«Диагональная» нумерация:
«![]() »
»![]() ,
где
,
где
![]() «
«![]() »
»![]() ,
,
![]() «
«![]() »
»![]() .
.
Этот способ нумерации иллюстрирует приведенная ниже таблица:
-

0
1
2
3
4
…
0
0
1
3
6
10
1
2
4
7
11
2
5
8
12
3
9
13
4
14
…
-
Нумерация на основе кодирования номеров элементов. Пусть
 и
и
 – представления в системе счисления
с основанием
– представления в системе счисления
с основанием
 (коды) номеров «
(коды) номеров « »
» и «
и « »
» (ноль кодируется пустым кодом нулевой
длины). Приведем эти коды к одинаковой
длине
(ноль кодируется пустым кодом нулевой
длины). Приведем эти коды к одинаковой
длине
 путем добавления к более короткому
коду лидирующих нулей. Определим
представление в той же системе счисления
(код) номера «
путем добавления к более короткому
коду лидирующих нулей. Определим
представление в той же системе счисления
(код) номера « »
» как
как
 .
В программных реализациях наиболее
часто используются значения
.
В программных реализациях наиболее
часто используются значения
 и
и
 .
.
-
Рекурсивно определенные нумерации. Приведем один из вариантов.
Пусть
![]() ,
«
,
«![]() »
»![]() ,
«
,
«![]() »
»![]() «
«![]() »
»![]() для всех
для всех
![]() .
Тогда
.
Тогда
![]()
![]() определим как свободное объединение
определим как свободное объединение
![]()
![]() ,
и нумерация
,
и нумерация
![]() будет такой: «
будет такой: «![]() »
»![]()
![]() «
«![]() »
»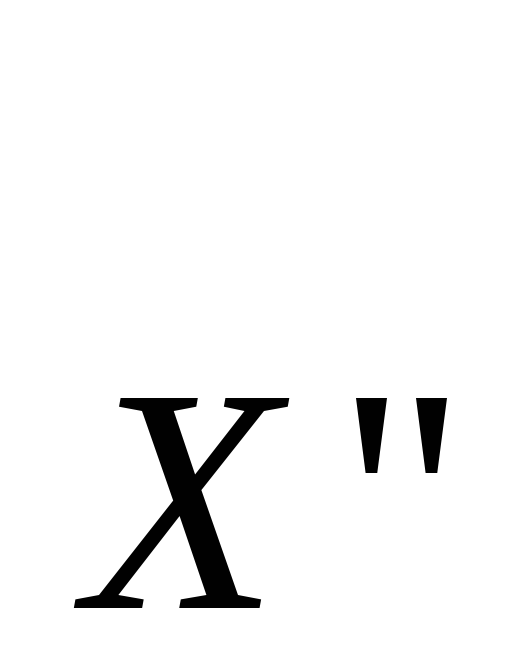 ,
для всех
,
для всех
![]() ,
а для всех
,
а для всех
![]() «
«![]() »
»![]() «
«![]() »
»![]() .
Нетрудно видеть, что для этой нумерации
представление номера «
.
Нетрудно видеть, что для этой нумерации
представление номера «![]() »
»![]() в двоичной системе счисления (двоичный
код) будет иметь вид:
в двоичной системе счисления (двоичный
код) будет иметь вид:
 ,
где
,
где
![]() «
«![]() »
»![]() ,
а
,
а
![]() – двоичное представление номера «
– двоичное представление номера «![]() »
»![]() .
.
Основными,
наиболее известными видами конечных
наборов элементов некоторого базового
конечного или счетного множества
объектов, являются кортежи
(упорядоченные конечные последовательности
элементов базового множества), комплекты
(неупорядоченные конечные последовательности
элементов базового множества), конечные
подмножества
базового множества, конечные
упорядоченные подмножества
базового множества. Введем обозначения
для различных множеств таких наборов
для конечного или счетного базового
множества
![]() .
.
![]() – множество всех
кортежей элементов счетного множества
– множество всех
кортежей элементов счетного множества
![]() ;
;
![]() – множество всех
кортежей из
– множество всех
кортежей из
![]() элементов счетного множества
элементов счетного множества
![]() ;
;
![]() – множество всех
комплектов элементов счетного множества
– множество всех
комплектов элементов счетного множества
![]() ;
;
![]() – множество всех
комплектов из
– множество всех
комплектов из
![]() элементов множества
элементов множества
![]() ;
;
![]() – множество всех
конечных подмножеств элементов множества
– множество всех
конечных подмножеств элементов множества
![]() ;
;
![]() – множество всех
подмножеств из
– множество всех
подмножеств из
![]() элементов множества
элементов множества
![]() ;
;
![]() – множество всех
конечных упорядоченных подмножеств
элементов множества
– множество всех
конечных упорядоченных подмножеств
элементов множества
![]() ;
;
![]() – множество всех
упорядоченных подмножеств из
– множество всех
упорядоченных подмножеств из
![]() элементов множества
элементов множества
![]() .
.
Соответственно,
сами объекты этих множеств – кортежи,
комплекты, конечные подмножества и
конечные упорядоченные подмножества
– будем, соответственно, изображать
так (далее все
![]() ):
):
![]() – кортеж элементов
множества
– кортеж элементов
множества
![]() ,
,
![]() – комплект элементов
множества
– комплект элементов
множества
![]() ,
,
![]() – конечное
подмножество элементов множества
– конечное
подмножество элементов множества
![]() ,
,
![]() – конечное
упорядоченное подмножество элементов
множества
– конечное
упорядоченное подмножество элементов
множества
![]() .
.
В качестве примера
использования этих обозначений рассмотрим
классификацию различных видов графов.
Известно, что в общем случае граф
определяется как упорядоченная пара,
которую составляют конечное множество
![]() «вершин» графа и объект
«вершин» графа и объект
![]() ,
характеризующий связи вершин графа. В
зависимости от математического уточнения
,
характеризующий связи вершин графа. В
зависимости от математического уточнения
![]() различают следующие варианты графов:
ориентированные и не ориентированные
графы, обыкновенные графы и мультиграфы,
с петлями (с возможностью связей вершин
самих с собой) и без петель. Не ограничивая
общности, будем считать, что множества
вершин различных графов – конечные
подмножества натуральных чисел:
различают следующие варианты графов:
ориентированные и не ориентированные
графы, обыкновенные графы и мультиграфы,
с петлями (с возможностью связей вершин
самих с собой) и без петель. Не ограничивая
общности, будем считать, что множества
вершин различных графов – конечные
подмножества натуральных чисел:
![]() .
Для простоты вначале предположим, что
рассматриваются только такие графы, в
которых нет изолированных вершин (т.е.
вершин, не находящихся в соответствующей
для этого вида графов связи с, вообще
говоря, другой вершиной графа). В этом
случае задание графа сводится к заданию
его компонента
.
Для простоты вначале предположим, что
рассматриваются только такие графы, в
которых нет изолированных вершин (т.е.
вершин, не находящихся в соответствующей
для этого вида графов связи с, вообще
говоря, другой вершиной графа). В этом
случае задание графа сводится к заданию
его компонента
![]() ,
зная который можно определить и множество
,
зная который можно определить и множество
![]() вершин этого графа. С учетом этих
замечаний получим варианты:
вершин этого графа. С учетом этих
замечаний получим варианты:
-
 – ориентированный
граф (орграф) с петлями,
– ориентированный
граф (орграф) с петлями, -
 – мультиорграф
с петлями,
– мультиорграф
с петлями, -
 – орграф без
петель,
– орграф без
петель, -
 – мультиорграф
без петель,
– мультиорграф
без петель, -
 – не ориентированный
граф (граф) с петлями,
– не ориентированный
граф (граф) с петлями, -
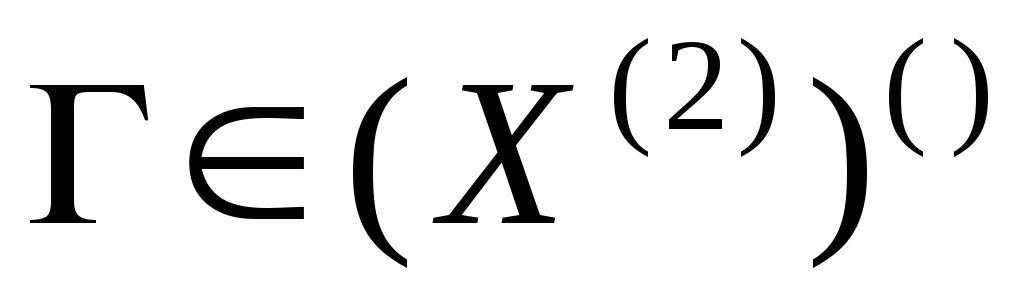 – мультиграф с
петлями.
– мультиграф с
петлями. -
 – граф без петель,
– граф без петель, -
 – мультиграф без
петель.
– мультиграф без
петель.
Если базовым
множеством является нумерованное
счетное множество, то можно без потери
общности считать, что базовым является
само множество натуральных чисел
![]() .
Далее рассматриваются некоторые
возможные способы нумерации множеств
основных структур с базисным множеством
.
Далее рассматриваются некоторые
возможные способы нумерации множеств
основных структур с базисным множеством
![]() .
Полагая, что из контекста всегда ясно,
о чем идет речь – об объекте определенной
структуры или об его номере, для
наглядности и простоты нотации сохраним
ранее введенные обозначения для различных
наборов и для их номеров в соответствующих
множествах. Наличие правого нижнего
индекса
.
Полагая, что из контекста всегда ясно,
о чем идет речь – об объекте определенной
структуры или об его номере, для
наглядности и простоты нотации сохраним
ранее введенные обозначения для различных
наборов и для их номеров в соответствующих
множествах. Наличие правого нижнего
индекса
![]() у закрывающей скобки означает, что
рассматривается номер объекта во
множестве наборов того же вида объектов
и с тем же числом элементов. Отсутствие
индекса означает, что рассматривается
номер объекта во множестве всех наборов
того же вида (с любым числом элементов).
Например,
у закрывающей скобки означает, что
рассматривается номер объекта во
множестве наборов того же вида объектов
и с тем же числом элементов. Отсутствие
индекса означает, что рассматривается
номер объекта во множестве всех наборов
того же вида (с любым числом элементов).
Например,
![]() обозначает номер комплекта из чисел
обозначает номер комплекта из чисел
![]() среди всех комплектов из четырех
натуральных чисел.
среди всех комплектов из четырех
натуральных чисел.
-
Нумерация множества кортежей из заданного числа
 натуральных чисел:
натуральных чисел:
![]() ,
,![]() для
для
![]() .
.
-
Нумерация множества всех возможных кортежей из любого числа
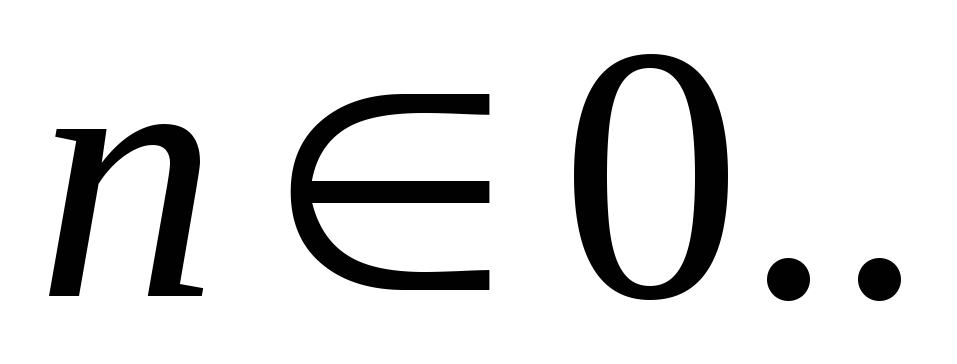 натуральных чисел:
натуральных чисел:
![]() .
.
-
Нумерация множества комплектов из заданного числа
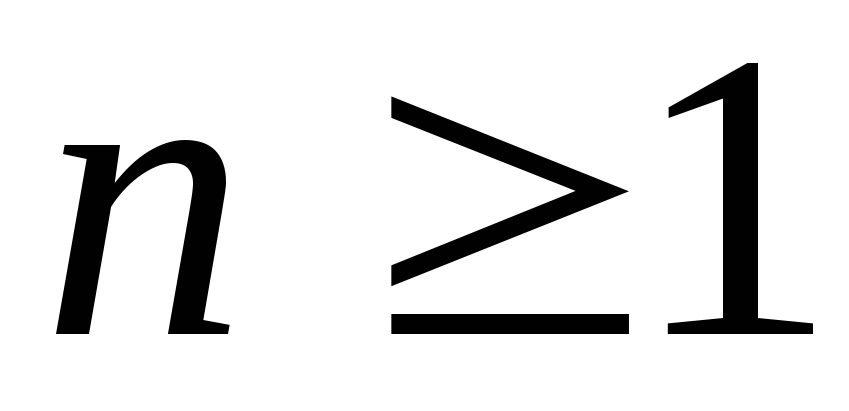 натуральных чисел. Так как порядок
перечисления элементов комплекта может
быть любым, не ограничивая общности,
предположим, что для комплекта натуральных
чисел
натуральных чисел. Так как порядок
перечисления элементов комплекта может
быть любым, не ограничивая общности,
предположим, что для комплекта натуральных
чисел
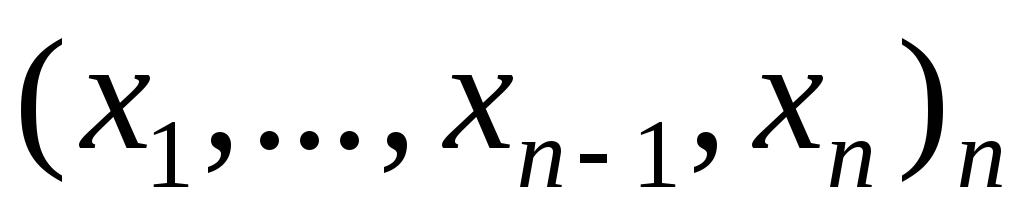 выполняется условие:
выполняется условие:

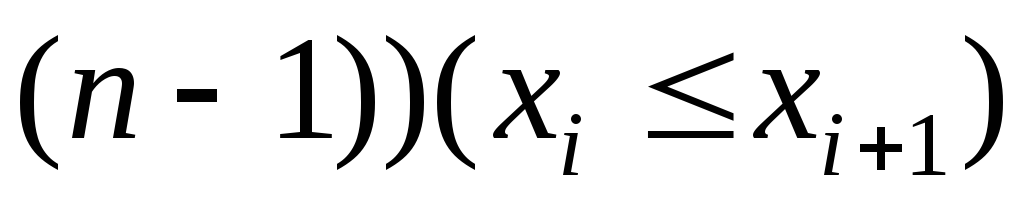 .
Нетрудно заметить, что разнообразие
комплектов из
.
Нетрудно заметить, что разнообразие
комплектов из
 натуральных чисел сводится к разнообразию
кортежей из
натуральных чисел сводится к разнообразию
кортежей из
 натуральных чисел:
натуральных чисел:
 ,
где
,
где
 ,
а для всех
,
а для всех

 .
. -
Нумерация множества всех возможных комплектов из любого числа
 натуральных чисел. Используя те же
построения, что и в п.3, сведем разнообразие
всех комплектов
натуральных чисел. Используя те же
построения, что и в п.3, сведем разнообразие
всех комплектов
 из любого числа натуральных чисел к
разнообразию всех возможных кортежей
из любого числа натуральных чисел к
разнообразию всех возможных кортежей
 натуральных чисел.
натуральных чисел. -
Нумерация множества подмножеств натуральных чисел с заданным числом элементов
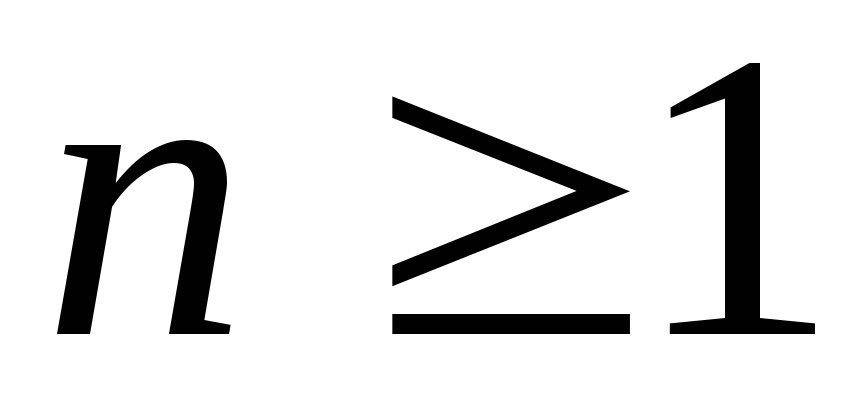 .
Аналогично случаю комплектов (п. 3),
упорядочим элементы подмножества
.
Аналогично случаю комплектов (п. 3),
упорядочим элементы подмножества
 натуральных чисел так, что выполняется
условие:
натуральных чисел так, что выполняется
условие:
 .
Тогда, очевидно, разнообразие подмножеств
натуральных чисел из
.
Тогда, очевидно, разнообразие подмножеств
натуральных чисел из
 элементов сводится к разнообразию
кортежей из
элементов сводится к разнообразию
кортежей из
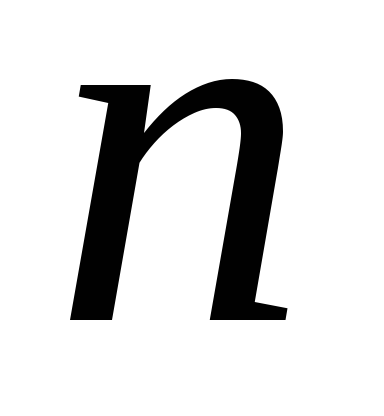 натуральных чисел:
натуральных чисел:

 ,
где
,
где
 ,
а для всех
,
а для всех

 .
. -
Нумерация множества всех возможных конечных подмножеств натуральных чисел с любым числом элементов
 .
Принцип построения кортежа натуральных
чисел
.
Принцип построения кортежа натуральных
чисел
 ,
представляющего подмножество
,
представляющего подмножество
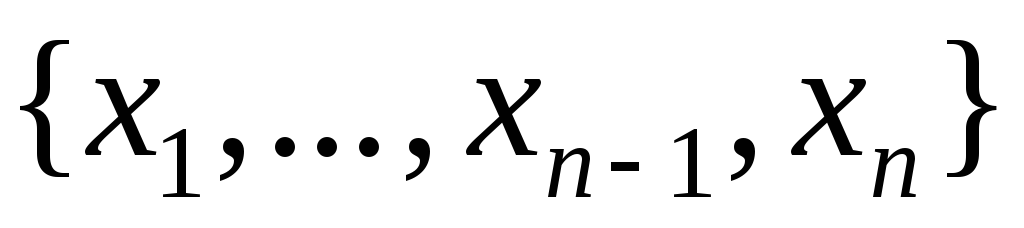 ,
тот же, что и в п.5.
,
тот же, что и в п.5. -
Нумерация множества упорядоченных подмножеств натуральных чисел с заданным числом элементов
 .
Разнообразие упорядоченных подмножеств
.
Разнообразие упорядоченных подмножеств

 натуральных чисел из
натуральных чисел из
 элементов сводится к разнообразию
кортежей
элементов сводится к разнообразию
кортежей
 из
из
 натуральных чисел следующим образом:
для всех
натуральных чисел следующим образом:
для всех

 .
Заметим, что, как и для объектов других
рассмотренных структур,
.
Заметим, что, как и для объектов других
рассмотренных структур,
 .
. -
Нумерация множества всех возможных конечных упорядоченных подмножеств натуральных чисел с любым числом элементов
 .
Принцип построения кортежа натуральных
чисел
.
Принцип построения кортежа натуральных
чисел
 ,
представляющего упорядоченное
подмножество
,
представляющего упорядоченное
подмножество
 ,
тот же, что и в п.7.
,
тот же, что и в п.7.
