- •Національний університет кораблебудування імені адмірала Макарова
- •Курсовий проект (робота)
- •1 Постановка задачі 3
- •2 Теоретичні відомості 7
- •Постановка задачі
- •1.2 Вирішувані задачі
- •2 Теоретичні відомості
- •2.1 Маткад
- •2.2 Періодичні сигнали
- •2.3 Неперіодичні сигнали
- •2.4 Спектральний метод аналізу лінійних радіотехнічних кіл
- •2.5 Часовий метод аналізу лінійних радіотехнічних кіл
- •3 Дослідження сигналу
- •4 Дослідження кола
- •Висновки
- •Список літератури
2.2 Періодичні сигнали
Електричні коливання, які представляють собою зміну в часі струму, напруги, заряду або іншої величини, що відображають повідомлення, називаються радіотехнічними сигналами.
Найбільш важливим класом неперервних детермінованих сигналів є періодичні сигнали. Періодичні сигнали при -∞<t<+∞ задовольняють умові:
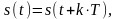 (1)
(1)
де k – будь-яке ціле число; Т– період сигналу. Найпростішим з періодичних сигналів, які широко використовуються в радіотехніці в якості вимірювальних, є гармонійне коливання:
 (2)
(2)
де А0 – амплітуда коливання ; ω0=2∙π∙f0 – кутова частота, f0 – циклічна частота; φ0 – початкова фаза коливання. Періодичний сигнал s(t) можна розкласти в ряд Фур'є. Тригонометричний ряд Фур'є визначається виразом:
 (3)
(3)
Коефіцієнти а0/2 (постійна складова), аn ( косинусні складові), bn ( синусні складові) розраховуються за формулами:
|
(4) |
|
(5) |
|
(6) |
Сукупність коефіцієнтів an і bn називається спектром періодичного сигналу. Тригонометричний ряд Фур'є може бути записаний і в іншій формі:
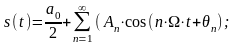 (7)
(7)
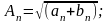 (8)
(8)
 (9)
(9)
Формули (8) і (9) показують, що коефіцієнти An і θn є, відповідно, модулем і аргументом комплексних чисел виду (an + jbn), тому при введенні формул в системі MathCAD доцільно використовувати функції модуля і аргументу комплексного числа і записувати формули (8) і (9) у вигляді:
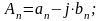 (10)
(10)
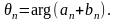 (11)
(11)
Коефіцієнти An, θn, an, bn, пов’язані між собою виразами:
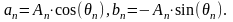 (12)
(12)
Сукупність коефіцієнтів An називається амплітудно-частотним спектром, а сукупність коефіцієнтів θn називається фазочастотним спектром періодичного сигналу s(t). Ряди (3) і (7) являють собою розкладання сигналу s(t) за гармонійними функціями. Самі функції виду:

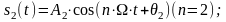 (13)
(13)
…

називають першою, другою та n-ю гармоніками, відповідно, A1, A2, ... An – амплітудами, а θ1, θ2 ,.. , θn – початковими фазами гармонік.
Як випливає з формул (3-9 ), частотний спектр періодичних сигналів є дискретним або лінійчатим. Тому при побудові амплітудних і фазових спектральних діаграм необхідно відзначати значення амплітуд і фаз тільки на частотах 0, Ὠ, 2 Ὠ, ... n Ὠ. Спектральні діаграми мають вигляд сукупності ліній ("паличок"), висоти яких дорівнюють відповідним значенням амплітуд і фаз.
Наведені вище формули є загальними і справедливі для періодичних сигналів будь-якого виду. У разі, якщо періодичний сигнал s(t) парний або непарний, наведені формули для розрахунку амплітудного і фазового спектрів значно спрощуються і мають наступний вигляд:
для парного сигналу:
 (14)
(14)
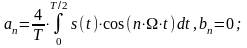 (15)
(15)
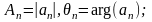 (16)
(16)
для непарного сигналу:
 (17)
(17)
 (18)
(18)
Формули ряду Фур'є (3) і (7) дозволяють точно синтезувати (відновити) сигнал з його спектру, проте в цих формулах виконується підсумовування нескінченно великого числа доданків. На практиці для синтезу сигналу використовують формулу з кінцевим числом доданків:
 (19)
(19)
де N – обране число;
для парних сигналів формула (19) приймає вигляд:
 (20)
(20)
для непарних сигналів
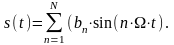 (21)
(21)
Основними енергетичними характеристиками дійсного сигналу s(t) є його потужність і енергія. Миттєва потужність сигналу:
 (22)
(22)
Енергія періодичного сигналу визначається за формулою:
 (23)
(23)
Середня за період потужність періодичного сигналу:
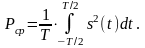 (24)
(24)
Ефективною (або активною) шириною спектра періодичного сигналу називається область частот, в якій зосереджена велика частина (не менше 90%) середньої потужності сигналу. Зазвичай активна ширина спектра визначається за обраним рівнем . Щоб знайти активну частину спектра, наприклад, за рівнем 0,05, необхідно на побудованій амплітудної спектральної діаграмі провести рівень, який відповідає 0,05 від значення амплітуди максимальної гармоніки, і визначити номер останньої гармоніки Na, величина якої перевищує обраний рівень. Потужність, що міститься в активній частині спектра, знаходиться за наступною формулою:
 (25)
(25)
При синтезі сигналу по активній частині спектра підсумовування в виразах (20, 21, 22) виконується до значення N=Na.
Різниця між вихідним сигналом s(t) і сигналом, синтезованим за активної частини спектра sa(t), можна оцінити чисельно за допомогою середньоквадратичного відхилення:
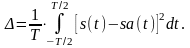 (26)
(26)