МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«Тюменский государственный нефтегазовый университет»
Институт менеджмента и бизнеса
Кафедра «Математические методы в экономике»
Математическая статистика
Методические указания для практических и лабораторных работ
по дисциплинам «Математика», «Теория вероятностей»,
«Теория вероятностей и математическая статистика»
для студентов всех форм обучения
всех направлений бакалавриата
Тюмень
ТюмГНГУ
2011
Утверждено редакционно-издательским советом
Тюменского государственного нефтегазового университета
Составители: Овчинникова с.В., к.С.Н., доцент
Сартакова А.В., ст. преподаватель
Федеральное государственное бюджетное образовательное учреждение высшего
профессионального образования
«Тюменский государственный нефтегазовый университет», 2011 г.
Введение
Получение высшего образования по всем направлениям бакалавриата требует высокой математической культуры, достаточного глубокого владения рядом специальных математических методов и умения непосредственного их применения в профессиональной деятельности. Методические указания рассчитаны на проведения практических и лабораторных занятий по данному разделу математики. Основной целью МУ является овладение методами математического аппарата для решения прикладных математических задач. В помощь студенту предлагается подробное решение практической работы «Расчет числовых характеристик выборки. Определения закона распределения случайной величины» и лабораторной работы «Построение теоретической линии регрессии в случае линейной корреляционной зависимости».
Также во время проведения практических и лабораторных занятий происходит формирование следующих общекультурных и профессиональных компетенций: способен к обобщению, анализу, восприятию информации, постановке цели и выбору путей её достижения, владеет культурой мышления, способен логически верно, аргументировано и ясно строить устную и письменную речь, способен собрать и проанализировать исходные данные, необходимые для расчета экономических и социально-экономических показателей, характеризующих деятельность хозяйствующих субъектов, способен осуществлять сбор, анализ и обработку данных, необходимых для решения поставленных экономических задач, способен использовать для решения коммуникативных задач современные технические средства и информационные технологии.
Практическая работа
«Расчет числовых характеристик выборки.
Определения закона распределения случайной величины»
Рейтинговая оценка работы:
выполнение – 10 баллов;
защита – 5 баллов.
Цель работы: ознакомление со способами построения рядов распределения и методом расчёта их числовых характеристик, применение критериев согласия.
Содержание работы:
Построить интервальный вариационный ряд. Гистограмму.
Перейти от интервального вариационного ряда к дискретному, заменив частичные интервалы их серединами. Построить полигон, кумуляту частот, частостей.
Найти эмпирическую функцию распределения.
Найти числовые характеристики выборки: моду, медиану, выборочное среднее, выборочное среднее квадратическое отклонение, коэффициент вариации, асимметрию, эксцесс.
Сделать предварительный выбор закона распределения случайной величины.
Проверить согласованность эмпирической и теоретической функций распределения выбранного закона распределения с помощью критериев согласия χ2-Пирсона, Колмогорова при уровне значимости α=0,05.
Определить интервальные оценки для генеральной средней, генерального среднего квадратического отклонения нормального закона распределения с надёжностью γ=0,95.
Методика выполнения практической работы.
В течение пятидесяти дней фиксировались цены акций компании “Фауна”. Отклонения от номинальной стоимости даны в таблице:
27,1 |
28 |
28,6 |
28,8 |
28,7 |
28,6 |
28,5 |
28,5 |
29,2 |
28,7 |
29 |
29 |
29,1 |
28,6 |
27,2 |
28,2 |
28,5 |
28,6 |
28,8 |
29,3 |
29,3 |
29,3 |
29,1 |
29 |
29,5 |
29,6 |
29,7 |
28,7 |
28,5 |
28,7 |
28,3 |
28,3 |
28,2 |
28,2 |
28,4 |
29,8 |
29,8 |
29,9 |
28,7 |
28,6 |
29,2 |
29 |
29,2 |
29,3 |
29,4 |
29,9 |
28,8 |
28,9 |
30,1 |
29,6 |
1. Для построения интервального ряда определим интервальный шаг выборки, воспользовавшись формулой Стерджеса h=(xmax-xmin)/(1+3,322lgn), где n – объём выборки (в нашем случае 50), xmax, xmin – соответственно наибольшее и наименьшее значения признака.
h=(30,1-27,1)/(1+3,322lg50)=0,45
0,5.
За начало первого интервала примем х1= xmin - h/2=26,9. В результате получим интервальный ряд.
Интервал (хi;хi+1] наблюдённых значений |
Частота ni |
Частость wi=ni/n |
26,9-27,4 |
2 |
0,04 |
27,4-27,9 |
0 |
0 |
27,9-28,4 |
7 |
0,14 |
28,4-28,9 |
18 |
0,36 |
28,9-29,4 |
14 |
0,28 |
29,4-29,9 |
8 |
0,16 |
29,9-30,4 |
1 |
0,02 |
Частота – это количество значений признака, встречающееся в данном интервале. Например, в интервал (27,9;28,4] попадает 7 значений отклонений цены от номинальной стоимости.
Гистограмма – это ступенчатая фигура, состоящая из прямоугольников. Их основаниями служат частичные интервалы, а высоты равны частотам (частостям). Ее график изображен на рис.1.
2
Рис.1. Гистограмма
xi |
27,15 |
27,65 |
28,15 |
28,65 |
29,15 |
29,65 |
30,15 |
Частота ni |
2 |
0 |
7 |
18 |
14 |
8 |
1 |
Частость wi=ni/n |
0,04 |
0 |
0,14 |
0,36 |
0,28 |
0,16 |
0,02 |
Полигон частот (многоугольник распределения) – ломаная, соединяющая точки с координатами (xi, ni) или (xi, wi). Его график отражен ниже на рис.2.
Рис.2. Полигон
частот
Кумулята – это
кривая накопленных частот (частостей).
Для её построения найдём
.
Ее графическое
изображение на рис.3.
xi |
27,15 |
27,65 |
28,15 |
28,65 |
29,15 |
29,65 |
30,15 |
Частость wi=ni/n |
0,04 |
0 |
0,14 |
0,36 |
0,28 |
0,16 |
0,02 |
Накопленная частость |
0,04 |
0,04 |
0,18 |
0,54 |
0,82 |
0,98 |
1 |
Рис.3. Кумулята
3. Эмпирической
функцией распределения F*(x)
называется относительная частота того,
что признак примет значение, меньшее
заданного x,
т.е. F*(x)=w(X<x)=
.
Она является аналогом функции распределения
случайной величины X.
Запишем эмпирическую функцию:
4. Модой Мо вариационного ряда называется варианта, которая имеет наибольшую частоту. Мо=28,65.
Медианой Ме вариационного ряда называется значение признака приходящееся на середину ранжированного ряда наблюдений.
Если n=2k+1 (нечётное число), то Ме=хк+1; если n=2k (чётное число), то Ме=(хк+1+хк)/2. Ме=28,65.
Выборочной средней
называют
среднее арифметическое значение признака
выборочной совокупности:
.
Выборочная дисперсия
Среднее
квадратическое отклонение
.
Найдём коэффициент
вариации
.
Определим коэффициент асимметрии, которая характеризует асимметрию полигона вариационного ряда
Вычислим эксцесс, показывающий степень “крутости” выборочного распределения относительно нормального распределения:
5.
Предварительный закон распределения
может определяться по величине
коэффициента вариации наблюдённых
данных. Например, для нормального закона
распределения он приближённо соответствует
интервалу [0,01; 0,40], для экспоненциального
– [0,6;1,3], для логарифмического –
[0,35;0,8].
Равенство выборочного
среднего и выборочной дисперсии может
служить основанием выбора пуассоновского
распределения. Для теоретического
показательного закона распределения
характерно равенство выборочного
среднего и выборочного среднего
квадратического отклонения. В случае
нормального закона распределения
асимметрия и эксцесс близки к нулю.
Гипотеза о нормальности закона
распределения может быть принята, если
выполняются неравенства:
и
,
где
Вычислим
Основываясь на значениях коэффициентов вариации (находится в интервале [0,01; 0,40]), асимметрии (близок к нулю), эксцесса (близок к нулю) можно предположить, что признак подчинён нормальному закону распределения.
Плотность вероятности
.
Тогда функция
распределения имеет вид
.
Здесь
- точечная оценка параметра а,
- параметра
.
6. Для строгой проверки гипотезы о нормальном распределении признака применим критерии согласия. Они позволяют ответить на вопрос являются ли неизбежные расхождения между эмпирическим и теоретическим распределениями случайными или теоретический закон подобран неудачно.
а) χ2-Пирсона. При его использовании сравниваются эмпирические ni и теоретические (предполагаемые) ni′ частоты.
Для расчёта вероятностей рi попадания случайной величины Х в интервал [xi, хi+1] используем функцию Лапласа (см. приложение 1) в соответствии со свойством нормального распределения:
Например,
Составим
вспомогательную таблицу:
i |
Интервалы [xi, хi+1] |
Эмпирические частоты ni |
Вероятности pi |
Теоретические частоты ni′=npi |
(ni- ni′)2 |
|
1 |
26,9-27,4 |
2 |
0,0073 |
|
5,31 |
0,47 |
2 |
27,4-27,9 |
0 |
0,0493 |
|||
3 |
27,9-28,4 |
7 |
0,1695 |
|||
4 |
28,4-28,9 |
18 |
0,3053 |
15,27 |
7,48 |
0,49 |
5 |
28,9-29,4 |
14 |
0,2893 |
14,47 |
0,22 |
0,01 |
6 |
29,4-29,9 |
8 |
0,1387 |
|
0,09 |
0,01 |
7 |
29,9-30,4 |
1 |
0,0352 |
|||
|
Σ |
50 |
0,9946 |
49,76 |
- |
χ2набл=0,99 |
Учитывая, что в рассматриваемом эмпирическом распределении частоты первого, второго и последнего интервалов (n1=2; n2=0 и n7=1) меньше пяти, при использовании критерия χ2 Пирсона целесообразно объединить указанные интервалы с соседними.
Итак, фактически
наблюдаемое значение статистики
=0,99.
Так как новое число
интервалов (с учётом объединения крайних)
m=4,
а нормальный закон имеет два параметра
a
и σ
(r=2),
то число степеней свободы k=m-r-1=4-2-1=1.
Соответствующее критическое значение
статистики при уровне значимости α=0,05
(см. приложение 5). Так как
,
то нет оснований отвергать гипотезу о
распределении случайной величины по
нормальному закону.
б) Воспользуемся критерием Колмогорова. При его использовании сравниваются эмпирическая F*(x) и теоретическая (предполагаемая) F(x)функции распределения. Для построения теоретической функции распределения для нормального закона распределения воспользуемся ее выражением через функцию Лапласа:
.
Например,
Составим вспомогательную таблицу
xi |
27,15 |
27,65 |
28,15 |
28,65 |
29,15 |
29,65 |
30,15 |
F*(x)= |
0,04 |
0,04 |
0,18 |
0,54 |
0,82 |
0,98 |
1 |
F(x) |
0,002 |
0,023 |
0,12 |
0,371 |
0,692 |
0,908 |
0,985 |
|F*(x)-F(x)| |
0,038 |
0,017 |
0,06 |
0,169 |
0,128 |
0,072 |
0,015 |
Вычислим значения D=max |F*(x)-F(x)|=0,169;
λнабл=
.
При уровне значимости α=0,05 табличное значение λα=1,36 (см. приложение 4). Так как λнабл< λα, то нет оснований отвергать гипотезу о распределении случайной величины по нормальному закону.
7. Для нахождения интервальных оценок параметров нормального распределения воспользуемся формулами
,
S(1-q)<σГ<S(1+q),
где
- исправленное среднее квадратическое
отклонение, t,q
– определяются по доверительной
вероятности γ и объёму выборки n
(см. приложения 2,3)
,
t(γ; n)=t(0,95; 50)=2,009, q(γ; n) =q(0,95; 50)=0,21.
;
0,482< σГ<0,738.
Первое неравенство означает, что математическое ожидание отклонения цены акции от номинальной с вероятностью 95% попадёт в интервал (28,68; 29,02).
Лабораторная работа
«Построение теоретической линии регрессии в случае линейной корреляционной зависимости»
Рейтинговая оценка работы:
выполнение – 10 баллов;
защита – 5 баллов.
Цель работы: ознакомиться с методикой построения линий регрессии с последующим анализом достоверности полученных параметров.
Содержание работы:
Построить корреляционное поле.
Найти частоты признаков.
Вычислить выборочный коэффициент корреляции.
Записать выборочные уравнения прямой и обратной линий регрессии.
Построить их на корреляционном поле.
Оценить коэффициент корреляции генеральной совокупности.
Проверить значимость выборочного коэффициента корреляции по критерию Стьюдента при уровне значимости α=0,05.
Найти корреляционное отношение.
Проверить значимость корреляционного отношения по критерию Стьюдента при уровне значимости α=0,05.
Проверить значимость уравнения прямой линии регрессии по критерию Фишера при уровне значимости α=0,05.
Методика выполнения лабораторной работы.
Для исследования зависимости объема производства (Y) от основных фондов (Х) получены статистические данные по 25 предприятиям за год.
Y X |
10 |
20 |
30 |
40 |
12 |
4 |
2 |
|
|
18 |
1 |
6 |
5 |
2 |
24 |
|
|
2 |
3 |
Необходимо установить вид зависимости между объемом производства и основными фондами.
Число 4 в таблице означает, что пара чисел (12, 10) встретилась в выборке 4 раза. Это число называется частотой и обозначается в дальнейшем nij. Значения признаков обозначаются хi, yj, i=1,…, l; j=1,…, m.
Для предварительного установления вида зависимости Y и X построим корреляционное поле (рис. 4). Нетрудно видеть, что оно располагается вдоль прямой. Это свидетельствует о линейности связи.
Рис. 4
Найдем частоты признаков ni=
, nj=
,
записав их в дополнительные столбец
и строку корреляционной таблицы. Объем
выборки
Y X |
10 |
20 |
30 |
40 |
ni |
|
|
|
||||||||||||
12 |
|
|
|
|
6 |
80 |
960 |
13,33 |
||||||||||||
18 |
|
|
|
|
14 |
360 |
6480 |
25,71 |
||||||||||||
24 |
|
|
|
|
5 |
180 |
4320 |
36 |
||||||||||||
nj |
5 |
8 |
7 |
5 |
n=25 |
|
11760 |
|
||||||||||||
|
66 |
132 |
138 |
108 |
|
|
|
|
||||||||||||
|
660 |
2640 |
4140 |
4320 |
11760 |
|
|
|
Выборочный коэффициент корреляции вычисляется по формуле
и показывает тесноту линейной связи
между признаками. Чем ближе rв
по абсолютной величине к 1, тем теснее
связь.
;
;
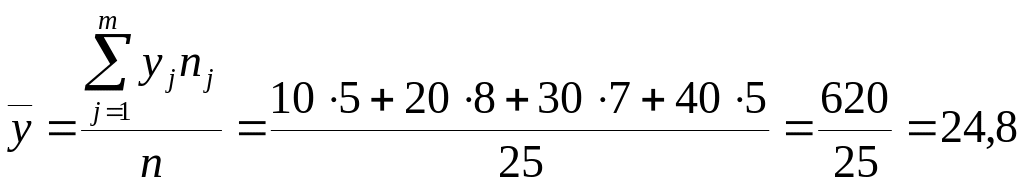Для вычисления
а) находят произведение частоты nij на варианту yj, которое записывают в правом верхнем углу клетки, содержащее значение частоты. Например, в правых верхних углах третьей строки записаны произведения 2·30=60, 3·40=120.
б) Складывают все числа, помещенные в правых верхних углах одной строки, и их сумму заносят в клетку этой же строки столбца . Например, в третьей строке 60+120=180.
в) Умножают варианту хi на полученные значения и заносят в клетку столбца . Например, в третьей строке 24·180=4320.
г) Сложив все числа
найденного столбца, получают сумму
.
Для контроля аналогичные вычисления производят по столбцам.
Найдем искомый выборочный коэффициент корреляции:
Коэффициент
детерминации
означает, что 55% общей дисперсии объема
производства обусловлено вариацией
основных фондов.
4. Выборочное уравнение прямой линии регрессии Y на Х имеет вид:
Запишем уравнение обратной линии регрессии Х на Y.
5. Построим эти прямые на корреляционном поле по двум точкам соответствующим наибольшему и наименьшему значениям вариант (рис.1).
6. Построим доверительный интервал коэффициента корреляции генеральной совокупности.
rв-Δ<rГ<rв+Δ,
где
.
0,47<rГ<1,01.
7. Проверим значимость выборочного коэффициента корреляции по критерию Стьюдента.
tкр(23;0,05)=2,07. (см. приложение 7)
|tнабл|> tкр нет основания отвергать гипотезу о коррелированности Х и Y.
8. Общей мерой тесноты связи линейной и нелинейной корреляционной зависимости между признаками является корреляционное отношение.
.
Чем ближе значение корреляционного отношения к 1, тем сильнее связь между признаками.
Вычислим условные
средние
занеся их в последнюю колонку корреляционной
таблицы. Например,
.
Равенство
свидетельствует, что корреляционная
связь между признаками линейная.
9. Проверим значимость корреляционного отношения по критерию Стьюдента.
tкр(k-2;α)=tкр(23;0,05)=2,07. (см. приложение 7)
|tнабл|> tкр нет основания отвергать гипотезу о коррелированности Х и Y.
10. Проверим значимость уравнения прямой линии регрессии по критерию Фишера.
где k – число оцениваемых параметров;
- сумма квадратов,
обусловленная регрессией;
- сумма квадратов
отклонений зависимой переменной от
средней;
- остаточная сумма
квадратов, характеризующая влияние
неучтенных факторов.
Вычислим
,
подставляя значения признака Х
в уравнение прямой линии регрессии
xi |
12 |
18 |
24 |
|
13,8 |
25,26 |
36,72 |
Уравнение линейной регрессии содержит два параметра, следовательно k=2.
;
Fкр= F(α, k1, k2)F(α, k-1, n-k)=F(0,05; 1; 23)=4,28 (см. приложение 6).
Fнабл>Fкр, следовательно, уравнение значимо описывает зависимость между признаками.
Задания для практической работы
№1. Даны значения овальности валиков ( в мк.): |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
25 |
29 |
33 |
21 |
29 |
25 |
29 |
27 |
29 |
31 |
31 |
31 |
29 |
|||||||||||
29 |
27 |
27 |
29 |
31 |
23 |
35 |
33 |
27 |
29 |
35 |
37 |
31 |
|||||||||||
29 |
27 |
29 |
29 |
29 |
29 |
31 |
29 |
27 |
25 |
31 |
25 |
27 |
|||||||||||
27 |
27 |
19 |
25 |
27 |
33 |
29 |
33 |
31 |
33 |
29 |
29 |
29 |
|||||||||||
29 |
29 |
35 |
27 |
27 |
29 |
27 |
29 |
31 |
29 |
31 |
29 |
31 |
|||||||||||
31 |
29 |
21 |
23 |
29 |
37 |
29 |
31 |
29 |
31 |
29 |
29 |
23 |
|||||||||||
29 |
39 |
29 |
39 |
39 |
27 |
31 |
37 |
31 |
29 |
27 |
31 |
27 |
|||||||||||
29 |
27 |
29 |
29 |
31 |
25 |
27 |
29 |
29 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
№2. Даны значения овальности валиков ( в мк.): |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
19 |
25 |
29 |
31 |
27 |
29 |
29 |
27 |
29 |
29 |
29 |
23 |
33 |
|||||||||||
31 |
27 |
33 |
37 |
33 |
29 |
31 |
31 |
35 |
19 |
37 |
29 |
25 |
|||||||||||
29 |
31 |
25 |
31 |
29 |
25 |
31 |
31 |
27 |
29 |
29 |
29 |
27 |
|||||||||||
29 |
23 |
33 |
29 |
29 |
29 |
27 |
29 |
31 |
29 |
31 |
29 |
29 |
|||||||||||
35 |
27 |
27 |
27 |
29 |
29 |
29 |
25 |
29 |
29 |
29 |
35 |
27 |
|||||||||||
31 |
35 |
29 |
29 |
27 |
27 |
23 |
31 |
29 |
35 |
27 |
29 |
31 |
|||||||||||
29 |
27 |
31 |
29 |
29 |
35 |
25 |
29 |
27 |
29 |
31 |
39 |
31 |
|||||||||||
27 |
21 |
23 |
27 |
25 |
31 |
29 |
29 |
33 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
№3. Даны значения диаметров шестерён обработанных на станке: |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
21 |
29 |
27 |
29 |
27 |
29 |
31 |
29 |
29 |
23 |
29 |
39 |
31 |
|||||||||||
29 |
31 |
29 |
31 |
29 |
31 |
33 |
31 |
25 |
27 |
25 |
31 |
29 |
|||||||||||
27 |
23 |
27 |
33 |
29 |
25 |
29 |
35 |
27 |
29 |
25 |
23 |
31 |
|||||||||||
29 |
27 |
33 |
29 |
37 |
25 |
31 |
31 |
29 |
31 |
35 |
27 |
29 |
|||||||||||
27 |
29 |
33 |
29 |
27 |
29 |
21 |
29 |
27 |
29 |
29 |
33 |
29 |
|||||||||||
27 |
27 |
29 |
27 |
27 |
31 |
29 |
25 |
29 |
33 |
31 |
29 |
29 |
|||||||||||
27 |
29 |
29 |
35 |
27 |
29 |
35 |
29 |
33 |
29 |
29 |
31 |
29 |
|||||||||||
31 |
31 |
27 |
23 |
31 |
31 |
29 |
29 |
19 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
№4. Даны значения температуры масла заднего моста автомобиля ГАЗ - 53 при средних скоростях: |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
4 |
8 |
10 |
6 |
8 |
6 |
10 |
8 |
10 |
10 |
10 |
12 |
12 |
|||||||||||
12 |
12 |
14 |
12 |
14 |
10 |
8 |
12 |
12 |
8 |
8 |
10 |
10 |
|||||||||||
10 |
10 |
8 |
8 |
10 |
8 |
14 |
10 |
8 |
12 |
12 |
6 |
12 |
|||||||||||
10 |
12 |
8 |
10 |
8 |
12 |
12 |
8 |
16 |
10 |
12 |
14 |
14 |
|||||||||||
8 |
10 |
12 |
10 |
8 |
10 |
8 |
16 |
8 |
10 |
10 |
12 |
10 |
|||||||||||
14 |
12 |
14 |
12 |
10 |
10 |
12 |
6 |
10 |
12 |
8 |
8 |
8 |
|||||||||||
8 |
14 |
12 |
8 |
10 |
10 |
6 |
6 |
10 |
8 |
14 |
10 |
4 |
|||||||||||
8 |
10 |
6 |
12 |
12 |
10 |
4 |
8 |
10 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
№5. Даны значения механической скорости проходки на ста скважинах при одном и том же числе израсходованных долот: |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
5 |
9 |
11 |
13 |
9 |
11 |
7 |
13 |
11 |
13 |
9 |
11 |
11 |
|||||||||||
15 |
9 |
13 |
15 |
11 |
9 |
17 |
7 |
13 |
11 |
11 |
11 |
9 |
|||||||||||
11 |
9 |
9 |
11 |
13 |
9 |
9 |
13 |
7 |
11 |
9 |
11 |
13 |
|||||||||||
13 |
7 |
17 |
11 |
11 |
15 |
9 |
13 |
9 |
5 |
11 |
9 |
13 |
|||||||||||
7 |
13 |
9 |
13 |
11 |
11 |
15 |
9 |
13 |
11 |
11 |
13 |
17 |
|||||||||||
13 |
15 |
9 |
9 |
11 |
13 |
11 |
5 |
15 |
11 |
11 |
15 |
9 |
|||||||||||
15 |
11 |
9 |
11 |
13 |
11 |
7 |
13 |
7 |
11 |
11 |
13 |
9 |
|||||||||||
9 |
13 |
9 |
13 |
13 |
9 |
11 |
9 |
13 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
№6. Даны значения механической скорости проходки на ста скважинах при одном и том же числе израсходованных долот: |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
7 |
11 |
5 |
9 |
11 |
13 |
11 |
13 |
9 |
11 |
9 |
11 |
9 |
|||||||||||
11 |
13 |
15 |
11 |
13 |
11 |
13 |
11 |
11 |
13 |
11 |
11 |
9 |
|||||||||||
5 |
9 |
11 |
9 |
11 |
7 |
13 |
11 |
13 |
13 |
11 |
13 |
13 |
|||||||||||
15 |
9 |
17 |
9 |
13 |
13 |
15 |
9 |
13 |
11 |
9 |
11 |
7 |
|||||||||||
11 |
7 |
5 |
9 |
11 |
11 |
9 |
15 |
11 |
13 |
17 |
7 |
13 |
|||||||||||
13 |
15 |
15 |
9 |
11 |
11 |
13 |
17 |
9 |
11 |
7 |
9 |
13 |
|||||||||||
9 |
11 |
9 |
7 |
7 |
9 |
11 |
17 |
11 |
13 |
9 |
13 |
9 |
|||||||||||
9 |
11 |
15 |
13 |
9 |
11 |
13 |
9 |
11 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
№7. Даны значения температуры смазочного масла коробки передач автомобиля ГАЗ - 53 при средних скоростях: |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
25 |
29 |
28 |
25 |
30 |
29 |
28 |
27 |
30 |
31 |
28 |
30 |
27 |
|||||||||||
30 |
32 |
30 |
33 |
31 |
28 |
33 |
30 |
33 |
33 |
31 |
30 |
29 |
|||||||||||
34 |
31 |
26 |
30 |
35 |
29 |
26 |
34 |
27 |
28 |
26 |
28 |
30 |
|||||||||||
29 |
31 |
26 |
31 |
31 |
30 |
27 |
29 |
33 |
29 |
24 |
29 |
31 |
|||||||||||
28 |
30 |
29 |
31 |
32 |
32 |
30 |
25 |
30 |
33 |
28 |
26 |
30 |
|||||||||||
28 |
34 |
31 |
30 |
32 |
36 |
34 |
30 |
32 |
30 |
32 |
27 |
27 |
|||||||||||
30 |
35 |
29 |
30 |
28 |
37 |
30 |
32 |
32 |
30 |
28 |
32 |
29 |
|||||||||||
34 |
30 |
26 |
33 |
32 |
27 |
29 |
26 |
31 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
№8. Даны значения температуры смазочного масла коробки передач автомобиля ГАЗ - 53 при средних скоростях: |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
26 |
31 |
32 |
26 |
30 |
33 |
30 |
36 |
26 |
32 |
29 |
31 |
27 |
|||||||||||
33 |
30 |
35 |
30 |
29 |
32 |
30 |
28 |
30 |
27 |
31 |
31 |
32 |
|||||||||||
30 |
29 |
33 |
30 |
26 |
25 |
27 |
30 |
33 |
24 |
31 |
30 |
28 |
|||||||||||
27 |
30 |
34 |
30 |
31 |
33 |
30 |
32 |
25 |
32 |
29 |
28 |
27 |
|||||||||||
23 |
25 |
33 |
30 |
35 |
24 |
30 |
29 |
30 |
37 |
28 |
28 |
29 |
|||||||||||
30 |
34 |
26 |
30 |
29 |
31 |
27 |
32 |
31 |
30 |
37 |
29 |
30 |
|||||||||||
34 |
29 |
30 |
35 |
31 |
31 |
30 |
32 |
23 |
24 |
32 |
25 |
28 |
|||||||||||
28 |
33 |
26 |
34 |
26 |
25 |
30 |
36 |
35 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
№9. Даны значения числа израсходованных долот на 100 скважин при механической скорости проходки 18м/час: |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
25 |
25 |
24 |
25 |
30 |
24 |
30 |
28 |
32 |
22 |
26 |
28 |
26 |
|||||||||||
31 |
31 |
25 |
33 |
25 |
29 |
29 |
30 |
29 |
30 |
28 |
23 |
30 |
|||||||||||
33 |
30 |
30 |
28 |
24 |
28 |
28 |
26 |
25 |
26 |
29 |
27 |
29 |
|||||||||||
27 |
34 |
29 |
32 |
26 |
29 |
28 |
29 |
30 |
27 |
30 |
28 |
32 |
|||||||||||
34 |
23 |
26 |
30 |
26 |
31 |
27 |
30 |
27 |
33 |
28 |
26 |
30 |
|||||||||||
30 |
31 |
29 |
27 |
30 |
30 |
29 |
27 |
26 |
28 |
29 |
36 |
29 |
|||||||||||
28 |
33 |
27 |
30 |
33 |
26 |
31 |
34 |
29 |
29 |
32 |
33 |
31 |
|||||||||||
29 |
24 |
26 |
28 |
28 |
29 |
27 |
29 |
29 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
№10. Даны значения числа израсходованных долот на 100 скважин при механической скорости проходки 18м/час: |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
28 |
30 |
28 |
27 |
28 |
29 |
29 |
32 |
30 |
29 |
29 |
31 |
28 |
|||||||||||
33 |
35 |
27 |
31 |
31 |
35 |
29 |
27 |
30 |
28 |
33 |
23 |
30 |
|||||||||||
31 |
27 |
30 |
30 |
32 |
24 |
28 |
30 |
29 |
30 |
26 |
25 |
31 |
|||||||||||
27 |
29 |
34 |
32 |
33 |
29 |
30 |
30 |
36 |
26 |
25 |
28 |
30 |
|||||||||||
29 |
34 |
27 |
32 |
29 |
31 |
30 |
31 |
26 |
25 |
29 |
31 |
28 |
|||||||||||
33 |
27 |
32 |
30 |
31 |
34 |
28 |
26 |
38 |
29 |
30 |
30 |
29 |
|||||||||||
27 |
31 |
30 |
28 |
34 |
30 |
26 |
30 |
30 |
28 |
32 |
30 |
29 |
|||||||||||
26 |
25 |
31 |
33 |
33 |
26 |
29 |
32 |
31 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
№11. 100 сверл были подвергнуты испытанию на твердость. При этом фиксировалась твердость лапки. Результаты испытания представлены следующим рядом значений: |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
36,1 |
37,2 |
31,2 |
38,6 |
34,1 |
37,2 |
30,6 |
37,2 |
35,1 |
36,9 |
34,3 |
35,2 |
||||||||||||
39,3 |
32,7 |
34,7 |
36,8 |
39,2 |
28,4 |
30,1 |
35,1 |
36,7 |
38,2 |
40,7 |
36,8 |
||||||||||||
29,3 |
28,3 |
40,3 |
34,6 |
37,3 |
32,1 |
41,3 |
33,3 |
40,4 |
34,8 |
37,1 |
41,2 |
||||||||||||
35,4 |
34,7 |
34,7 |
43,3 |
41,2 |
35,4 |
40,8 |
37 |
39,1 |
33,2 |
39,2 |
37,3 |
||||||||||||
34,7 |
39,3 |
36,9 |
32,8 |
34,8 |
36,8 |
38,4 |
37 |
40,6 |
42,1 |
38,1 |
36,7 |
||||||||||||
32,7 |
31,3 |
32,4 |
41,3 |
30,3 |
39,3 |
37,3 |
32,5 |
34,3 |
39,3 |
33,1 |
33,4 |
||||||||||||
36,8 |
32 |
39,4 |
36,3 |
35,4 |
37,3 |
34,7 |
32,4 |
36,7 |
39 |
30,9 |
35,3 |
||||||||||||
39,4 |
35,4 |
36,8 |
41,2 |
45 |
33,4 |
33,4 |
38,6 |
36,9 |
36,1 |
39,3 |
32,7 |
||||||||||||
38,3 |
43,4 |
35,4 |
37,1 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
№12. 100 сверл были подвергнуты испытанию на твердость. При этом фиксировалась твердость лапки. Результаты испытания представлены следующим рядом значений: |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
14,5 |
14,6 |
15,1 |
15,5 |
16,3 |
16,8 |
17,9 |
16,3 |
14,5 |
14,9 |
13,6 |
15,4 |
||||||||||||
15,5 |
11,3 |
15,5 |
18,1 |
16,8 |
12,2 |
15,2 |
15,7 |
15,2 |
16,9 |
15,7 |
17,7 |
||||||||||||
12,8 |
14,2 |
15,5 |
16,1 |
14,3 |
16,5 |
14,5 |
17,8 |
14,2 |
16,3 |
11,7 |
13,2 |
||||||||||||
17,9 |
14,9 |
15,2 |
17,3 |
16,9 |
16,9 |
17,4 |
17,5 |
14,6 |
16,5 |
14,3 |
19,2 |
||||||||||||
13,2 |
16,1 |
14,6 |
14,3 |
15,1 |
15,9 |
11,3 |
17,7 |
16,8 |
15,7 |
18,7 |
16,8 |
||||||||||||
15,3 |
15,9 |
16,6 |
14,8 |
15,9 |
11,7 |
13,6 |
18,2 |
11,6 |
13,9 |
14,1 |
15,2 |
||||||||||||
15,3 |
18,5 |
17,4 |
13,4 |
11,2 |
13,8 |
12,6 |
13,5 |
13,8 |
12,9 |
15,4 |
15,3 |
||||||||||||
16,9 |
15,4 |
14,3 |
14,9 |
19,8 |
16,6 |
19,5 |
15,2 |
16,5 |
13,1 |
15,1 |
14,9 |
||||||||||||
16,6 |
16,2 |
15,5 |
14,8 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
№13. Даны значения внутреннего диаметра гайки в мм: |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
4,49 |
4,45 |
4,63 |
4,79 |
4,68 |
4,63 |
4,55 |
4,51 |
4,46 |
4,45 |
4,68 |
4,71 |
||||||||||||
4,43 |
4,63 |
4,54 |
4,36 |
4,54 |
4,55 |
4,62 |
4,66 |
4,77 |
4,69 |
4,52 |
4,57 |
||||||||||||
4,63 |
4,78 |
4,42 |
4,45 |
4,65 |
4,43 |
4,62 |
4,55 |
4,42 |
4,28 |
4,69 |
4,73 |
||||||||||||
4,66 |
4,48 |
4,49 |
4,32 |
4,17 |
4,65 |
4,52 |
4,95 |
4,92 |
4,48 |
4,65 |
4,46 |
||||||||||||
4,57 |
4,68 |
4,77 |
4,13 |
4,59 |
4,51 |
4,43 |
4,46 |
4,61 |
4,32 |
4,59 |
4,48 |
||||||||||||
4,49 |
4,51 |
4,31 |
4,68 |
4,87 |
4,48 |
4,53 |
4,54 |
4,52 |
4,41 |
4,39 |
4,16 |
||||||||||||
4,25 |
4,38 |
4,35 |
4,25 |
4,38 |
4,22 |
4,34 |
4,74 |
4,85 |
4,53 |
4,36 |
4,27 |
||||||||||||
4,55 |
4,13 |
4,55 |
4,52 |
4,49 |
4,79 |
4,75 |
4,74 |
4,69 |
4,56 |
4,59 |
4,53 |
||||||||||||
4,12 |
4,57 |
4,52 |
4,82 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
№14. Даны значения ширины пера круглой плашки в мм: |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
3,59 |
3,48 |
3,66 |
3,59 |
3,53 |
3,49 |
3,51 |
3,31 |
3,68 |
3,87 |
3,57 |
3,68 |
||||||||||||
3,51 |
3,43 |
3,46 |
3,61 |
3,32 |
3,65 |
3,52 |
3,95 |
3,92 |
3,48 |
3,65 |
3,46 |
||||||||||||
3,69 |
3,73 |
3,52 |
3,49 |
3,79 |
3,66 |
3,48 |
3,49 |
3,32 |
3,17 |
3,63 |
3,42 |
||||||||||||
3,43 |
3,62 |
3,55 |
3,42 |
3,48 |
3,55 |
3,62 |
3,66 |
3,77 |
3,69 |
3,52 |
3,57 |
||||||||||||
3,6 |
3,7 |
3,55 |
3,13 |
3,55 |
3,43 |
3,69 |
3,54 |
3,36 |
3,54 |
3,49 |
3,45 |
||||||||||||
3,63 |
3,55 |
3,51 |
3,46 |
3,45 |
3,25 |
3,38 |
3,35 |
3,36 |
3,38 |
3,02 |
3,34 |
||||||||||||
3,99 |
3,33 |
3,23 |
3,19 |
3,88 |
3,27 |
3,14 |
3,83 |
3,96 |
3,85 |
3,74 |
3,85 |
||||||||||||
3,77 |
3,13 |
3,59 |
3,78 |
3,45 |
3,65 |
3,52 |
3,57 |
3,22 |
3,65 |
3,79 |
3,68 |
||||||||||||
3,75 |
3,74 |
3,69 |
3,53 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
№15. Даны значения обследуемого признака Х - толщины резца в мм: |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
25,3 |
25,7 |
28,7 |
23,2 |
26,9 |
21,7 |
22,8 |
22,2 |
23,6 |
24,5 |
28,5 |
23,6 |
||||||||||||
23,2 |
24,2 |
25,2 |
25,4 |
24,6 |
27,4 |
28,2 |
23,1 |
24,6 |
27,5 |
24,9 |
25,5 |
||||||||||||
23,4 |
21,6 |
25,1 |
24,3 |
24,6 |
24,8 |
26,2 |
25,7 |
26,9 |
25,5 |
26,2 |
23,9 |
||||||||||||
26,2 |
24,3 |
25,2 |
24,3 |
26,3 |
23,8 |
24,1 |
25,3 |
25,9 |
24,8 |
27,9 |
26,5 |
||||||||||||
22,6 |
25,2 |
25,9 |
21,3 |
29,2 |
24,9 |
24,5 |
27,7 |
21,3 |
27,3 |
23,5 |
25,4 |
||||||||||||
25,2 |
27,8 |
26,6 |
25,5 |
26,3 |
23,8 |
25,3 |
24,8 |
26,8 |
25,2 |
27,3 |
24,2 |
||||||||||||
22,5 |
24,8 |
25,9 |
25,7 |
26,5 |
26,9 |
26,3 |
25,5 |
26,8 |
24,9 |
26,2 |
27,1 |
||||||||||||
26,8 |
26,1 |
27,4 |
24,9 |
25,1 |
26,5 |
26,9 |
25,5 |
26,8 |
26,6 |
27,7 |
29,5 |
||||||||||||
25,7 |
25,4 |
25,1 |
24,5 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
№16. Даны значения обследуемого признака Х - себестоимости ед. продукции в руб: |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
73 |
77 |
78 |
88 |
76 |
78 |
86 |
96 |
84 |
79 |
77 |
75 |
90 |
|||||||||||||||||||||||
79 |
87 |
83 |
79 |
73 |
92 |
89 |
75 |
84 |
86 |
85 |
74 |
77 |
|||||||||||||||||||||||
81 |
87 |
85 |
92 |
80 |
88 |
76 |
79 |
71 |
88 |
83 |
76 |
76 |
|||||||||||||||||||||||
89 |
79 |
83 |
88 |
79 |
90 |
76 |
75 |
91 |
83 |
82 |
84 |
85 |
|||||||||||||||||||||||
87 |
89 |
85 |
85 |
79 |
92 |
86 |
84 |
77 |
92 |
93 |
91 |
91 |
|||||||||||||||||||||||
85 |
84 |
87 |
81 |
83 |
80 |
82 |
76 |
81 |
90 |
75 |
83 |
87 |
|||||||||||||||||||||||
95 |
77 |
91 |
84 |
84 |
83 |
93 |
73 |
79 |
71 |
88 |
88 |
74 |
|||||||||||||||||||||||
82 |
73 |
78 |
83 |
95 |
82 |
78 |
81 |
88 |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
№17. Даны значения обследуемого признака Х - себестоимости в руб: |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
82 |
83 |
73 |
76 |
79 |
89 |
95 |
85 |
84 |
95 |
75 |
77 |
90 |
|||||||||||||||||||||||
88 |
81 |
78 |
86 |
84 |
77 |
83 |
88 |
84 |
86 |
85 |
87 |
84 |
|||||||||||||||||||||||
87 |
73 |
76 |
83 |
87 |
89 |
73 |
78 |
76 |
76 |
74 |
88 |
82 |
|||||||||||||||||||||||
79 |
89 |
82 |
79 |
77 |
79 |
97 |
84 |
80 |
75 |
81 |
73 |
78 |
|||||||||||||||||||||||
76 |
84 |
75 |
90 |
83 |
77 |
84 |
90 |
92 |
85 |
91 |
85 |
79 |
|||||||||||||||||||||||
71 |
85 |
87 |
82 |
94 |
92 |
76 |
93 |
90 |
73 |
82 |
77 |
92 |
|||||||||||||||||||||||
93 |
88 |
84 |
81 |
93 |
81 |
91 |
78 |
79 |
81 |
88 |
92 |
84 |
|||||||||||||||||||||||
88 |
76 |
73 |
85 |
83 |
96 |
74 |
83 |
83 |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
№18. Даны значения обследуемого признака Х - себестоимости в руб: |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
80 |
81 |
83 |
92 |
88 |
86 |
85 |
93 |
81 |
76 |
92 |
93 |
84 |
|||||||||||||||||||||||
75 |
83 |
78 |
83 |
86 |
81 |
92 |
78 |
96 |
86 |
84 |
83 |
93 |
|||||||||||||||||||||||
92 |
93 |
84 |
84 |
81 |
84 |
76 |
77 |
76 |
74 |
80 |
91 |
88 |
|||||||||||||||||||||||
75 |
95 |
76 |
78 |
75 |
77 |
65 |
75 |
86 |
83 |
83 |
77 |
85 |
|||||||||||||||||||||||
73 |
76 |
74 |
92 |
91 |
86 |
83 |
79 |
89 |
83 |
92 |
83 |
79 |
|||||||||||||||||||||||
87 |
86 |
90 |
90 |
82 |
78 |
87 |
76 |
89 |
84 |
90 |
82 |
79 |
|||||||||||||||||||||||
89 |
95 |
81 |
89 |
78 |
91 |
88 |
83 |
81 |
92 |
73 |
70 |
88 |
|||||||||||||||||||||||
80 |
73 |
81 |
84 |
85 |
89 |
81 |
74 |
85 |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
№19. Имеются следующие данные о производительности труда 100 рабочих (в шт.): |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
78 |
90 |
90 |
86 |
81 |
77 |
83 |
86 |
74 |
82 |
85 |
92 |
86 |
|||||||||||||||||||||||
83 |
73 |
73 |
84 |
85 |
88 |
81 |
78 |
83 |
88 |
76 |
87 |
85 |
|||||||||||||||||||||||
83 |
76 |
77 |
86 |
84 |
83 |
84 |
83 |
89 |
87 |
76 |
82 |
89 |
|||||||||||||||||||||||
82 |
81 |
76 |
83 |
87 |
71 |
78 |
85 |
84 |
81 |
83 |
88 |
81 |
|||||||||||||||||||||||
92 |
82 |
80 |
79 |
82 |
86 |
74 |
91 |
78 |
93 |
84 |
81 |
84 |
|||||||||||||||||||||||
76 |
74 |
81 |
93 |
83 |
92 |
91 |
83 |
79 |
84 |
78 |
92 |
75 |
|||||||||||||||||||||||
84 |
81 |
78 |
76 |
90 |
88 |
86 |
85 |
84 |
89 |
73 |
75 |
80 |
|||||||||||||||||||||||
87 |
89 |
74 |
89 |
83 |
80 |
96 |
79 |
90 |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
№20. Имеются следующие данные о производительности труда 100 рабочих ( в шт.): |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
93 |
93 |
90 |
74 |
97 |
80 |
87 |
77 |
74 |
82 |
82 |
76 |
83 |
|||||||||||||||||||||||
84 |
82 |
85 |
81 |
84 |
85 |
81 |
88 |
83 |
88 |
92 |
76 |
83 |
|||||||||||||||||||||||
86 |
79 |
76 |
83 |
84 |
81 |
84 |
83 |
89 |
92 |
78 |
93 |
74 |
|||||||||||||||||||||||
79 |
89 |
73 |
90 |
85 |
79 |
78 |
81 |
93 |
86 |
83 |
83 |
76 |
|||||||||||||||||||||||
81 |
77 |
81 |
71 |
82 |
91 |
84 |
85 |
81 |
78 |
88 |
84 |
75 |
|||||||||||||||||||||||
83 |
74 |
81 |
83 |
76 |
87 |
88 |
91 |
74 |
88 |
89 |
87 |
90 |
|||||||||||||||||||||||
84 |
81 |
85 |
73 |
85 |
90 |
83 |
86 |
82 |
87 |
89 |
83 |
82 |
|||||||||||||||||||||||
96 |
84 |
81 |
92 |
81 |
75 |
79 |
87 |
80 |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
№21. Даны значения отклонений диаметра ролика от номинального размера ( в мм. ): |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
0,01 |
0,01 |
0,13 |
0,05 |
0,11 |
0,08 |
0,17 |
0,05 |
0,03 |
0,11 |
0,13 |
0,14 |
||||||||||||||||||||||||
0,14 |
0,06 |
0,12 |
0,13 |
0,04 |
0,03 |
0,05 |
0,11 |
0,06 |
0,1 |
0,05 |
0,06 |
||||||||||||||||||||||||
0,12 |
0,08 |
0,04 |
0,08 |
0,08 |
0,13 |
0,13 |
0,09 |
0,16 |
0,08 |
0,01 |
0,1 |
||||||||||||||||||||||||
0,15 |
0,12 |
0,17 |
0,17 |
0,16 |
0,04 |
0,06 |
0,09 |
0,03 |
0,04 |
0,04 |
0,11 |
||||||||||||||||||||||||
0,05 |
0,07 |
0,04 |
0,11 |
0,05 |
0,08 |
0,1 |
0,14 |
0,06 |
0,09 |
0,03 |
0,06 |
||||||||||||||||||||||||
0,09 |
0,09 |
0,12 |
0,09 |
0,1 |
0,06 |
0,11 |
0,09 |
0,14 |
0,06 |
0,1 |
0,06 |
||||||||||||||||||||||||
0,08 |
0,12 |
0,08 |
0,08 |
0,08 |
0,02 |
0,09 |
0,06 |
0,12 |
0,1 |
0,11 |
0,09 |
||||||||||||||||||||||||
0,1 |
0,11 |
0,13 |
0,09 |
0,04 |
0,09 |
0,02 |
0,07 |
0,07 |
0,15 |
0,07 |
0,07 |
||||||||||||||||||||||||
0,06 |
0,14 |
0,06 |
0,15 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
№22. Даны значения производительности труда 100 рабочих ( в шт. ): |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
87 |
81 |
71 |
73 |
90 |
89 |
75 |
84 |
88 |
85 |
86 |
92 |
83 |
|||||||||||||||||||||||
75 |
81 |
75 |
78 |
89 |
87 |
87 |
83 |
73 |
96 |
82 |
92 |
76 |
|||||||||||||||||||||||
76 |
91 |
90 |
85 |
78 |
98 |
83 |
76 |
85 |
81 |
78 |
83 |
74 |
|||||||||||||||||||||||
86 |
78 |
75 |
74 |
85 |
75 |
82 |
78 |
90 |
70 |
88 |
74 |
74 |
|||||||||||||||||||||||
92 |
87 |
88 |
83 |
84 |
76 |
91 |
78 |
93 |
83 |
82 |
91 |
84 |
|||||||||||||||||||||||
77 |
75 |
83 |
91 |
85 |
76 |
79 |
78 |
81 |
86 |
89 |
91 |
85 |
|||||||||||||||||||||||
97 |
83 |
78 |
85 |
88 |
84 |
76 |
79 |
91 |
93 |
70 |
84 |
81 |
|||||||||||||||||||||||
88 |
83 |
85 |
87 |
73 |
83 |
93 |
80 |
92 |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
№23. Получены следующие данные о суточном дебите нефти наблюдаемой скважины ( в т/сут.): |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
16 |
13 |
11 |
15 |
18 |
19 |
21 |
22 |
23 |
20 |
18 |
17 |
15 |
|||||||||||||||||||||||
18 |
17 |
19 |
15 |
13 |
23 |
25 |
28 |
12 |
14 |
16 |
17 |
20 |
|||||||||||||||||||||||
20 |
19 |
18 |
18 |
22 |
22 |
22 |
24 |
1 |
15 |
14 |
10 |
12 |
|||||||||||||||||||||||
18 |
26 |
19 |
22 |
19 |
21 |
23 |
20 |
22 |
24 |
17 |
16 |
14 |
|||||||||||||||||||||||
22 |
23 |
18 |
15 |
11 |
16 |
17 |
15 |
13 |
16 |
17 |
18 |
21 |
|||||||||||||||||||||||
14 |
15 |
19 |
17 |
18 |
16 |
13 |
15 |
17 |
21 |
21 |
27 |
19 |
|||||||||||||||||||||||
19 |
22 |
24 |
25 |
20 |
21 |
24 |
19 |
25 |
20 |
13 |
16 |
17 |
|||||||||||||||||||||||
16 |
18 |
15 |
15 |
20 |
22 |
23 |
26 |
17 |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
№24.Полученные данные о работе дебитах газовой скважины ( в тыс м3/сут. ): |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
550 |
550 |
551 |
551 |
550 |
551 |
562 |
550 |
546 |
558 |
562 |
551 |
||||||||||||||||||||||||
542 |
539 |
537 |
543 |
540 |
560 |
566 |
556 |
546 |
556 |
556 |
534 |
||||||||||||||||||||||||
560 |
558 |
545 |
550 |
548 |
540 |
541 |
551 |
549 |
551 |
550 |
552 |
||||||||||||||||||||||||
554 |
551 |
547 |
552 |
559 |
557 |
546 |
552 |
550 |
557 |
547 |
553 |
||||||||||||||||||||||||
547 |
554 |
567 |
558 |
563 |
563 |
563 |
562 |
547 |
558 |
569 |
552 |
||||||||||||||||||||||||
560 |
550 |
539 |
549 |
539 |
565 |
559 |
547 |
540 |
554 |
545 |
552 |
||||||||||||||||||||||||
554 |
546 |
553 |
555 |
550 |
550 |
553 |
557 |
555 |
545 |
530 |
542 |
||||||||||||||||||||||||
548 |
533 |
558 |
568 |
538 |
548 |
564 |
552 |
554 |
554 |
549 |
545 |
||||||||||||||||||||||||
543 |
558 |
544 |
535 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
№25. Данные по обводненности продукции нефтяных скважин ( % ):
|
|||||||||||||||||||||||||||||||||||
61,2 |
61,4 |
60,2 |
61,2 |
61,3 |
60,4 |
61,4 |
60,8 |
61,2 |
60,6 |
61,6 |
60,2 |
||||||||||||||||||||||||
60 |
61,2 |
60,5 |
61 |
61,4 |
61,1 |
60,9 |
61,5 |
61,4 |
60,6 |
61,2 |
60,1 |
||||||||||||||||||||||||
60,3 |
61,3 |
60,6 |
61,7 |
60,6 |
61,2 |
60,8 |
61,3 |
61 |
61,2 |
60,5 |
61,4 |
||||||||||||||||||||||||
61,2 |
61,2 |
61,3 |
60,9 |
61,4 |
60,7 |
61,2 |
60,9 |
61,3 |
61,1 |
61,3 |
61,5 |
||||||||||||||||||||||||
61,6 |
61 |
61,7 |
61,1 |
60,9 |
61,5 |
61,6 |
61,4 |
61,4 |
61,4 |
61,6 |
61,3 |
||||||||||||||||||||||||
60,9 |
62,2 |
61,1 |
61,2 |
68,9 |
61,5 |
61,7 |
62,3 |
62,3 |
62,2 |
61,7 |
62,3 |
||||||||||||||||||||||||
62,1 |
62,6 |
61,6 |
62,5 |
62,4 |
62,1 |
62,3 |
62,2 |
62,3 |
62,2 |
61,9 |
61,5 |
||||||||||||||||||||||||
61,3 |
60,3 |
60,7 |
61,3 |
61,1 |
61,3 |
60,7 |
61,3 |
60,9 |
61,3 |
61,1 |
61,7 |
||||||||||||||||||||||||
62,5 |
62,8 |
62,6 |
61,8 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
№26. Данные о коэффициенте эксплуатации фонтанирующих скважин: |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
0,9 |
0,94 |
0,88 |
0,91 |
0,89 |
0,93 |
0,96 |
0,98 |
0,96 |
0,9 |
0,92 |
0,92 |
||||||||||||||||||||||||
0,91 |
0,94 |
0,9 |
0,88 |
0,9 |
0,93 |
0,95 |
0,99 |
0,91 |
0,94 |
1 |
0,83 |
||||||||||||||||||||||||
0,91 |
0,89 |
0,97 |
0,9 |
0,93 |
0,95 |
1 |
0,83 |
0,85 |
0,87 |
0,9 |
0,92 |
||||||||||||||||||||||||
0,92 |
0,89 |
0,99 |
0,99 |
0,94 |
0,98 |
0,92 |
0,94 |
0,84 |
0,96 |
0,91 |
0,84 |
||||||||||||||||||||||||
0,98 |
0,85 |
0,92 |
0,88 |
1 |
0,87 |
0,93 |
0,97 |
0,86 |
0,99 |
0,91 |
0,89 |
||||||||||||||||||||||||
0,95 |
1 |
0,83 |
0,85 |
0,87 |
0,92 |
0,92 |
0,91 |
0,86 |
0,92 |
0,91 |
0,94 |
||||||||||||||||||||||||
0,98 |
0,92 |
0,94 |
0,84 |
0,96 |
0,91 |
0,84 |
0,86 |
0,9 |
0,87 |
0,9 |
0,87 |
||||||||||||||||||||||||
0,91 |
0,86 |
0,92 |
0,93 |
0,95 |
0,96 |
0,88 |
0,97 |
0,95 |
0,97 |
0,9 |
0,93 |
||||||||||||||||||||||||
0,86 |
0,9 |
0,88 |
0,9 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
№27. Получены данные о суточной добыче нефти в т/сут.: |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
85 |
76 |
80 |
84 |
88 |
89 |
91 |
79 |
86 |
90 |
88 |
84 |
85 |
86 |
89 |
88 |
84 |
90 |
85 |
87 |
90 |
89 |
85 |
91 |
87 |
81 |
88 |
91 |
89 |
98 |
91 |
88 |
87 |
74 |
81 |
87 |
90 |
88 |
86 |
88 |
91 |
97 |
88 |
77 |
88 |
82 |
85 |
84 |
74 |
80 |
84 |
91 |
84 |
90 |
90 |
87 |
77 |
83 |
89 |
91 |
92 |
88 |
94 |
90 |
82 |
88 |
81 |
83 |
89 |
94 |
96 |
89 |
88 |
95 |
99 |
95 |
89 |
95 |
78 |
81 |
86 |
90 |
92 |
93 |
90 |
83 |
79 |
89 |
75 |
82 |
90 |
78 |
85 |
76 |
84 |
99 |
91 |
87 |
85 |
86 |
|
|
|
|
№28. Имеются данные о пластовом давлении ( атм. ) нефтяной залежи: |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
195 |
157 |
115 |
126 |
135 |
146 |
152 |
155 |
156 |
102 |
159 |
147 |
117 |
132 |
142 |
148 |
158 |
163 |
165 |
156 |
102 |
196 |
145 |
154 |
155 |
153 |
148 |
158 |
137 |
130 |
110 |
116 |
120 |
149 |
148 |
143 |
154 |
151 |
103 |
197 |
128 |
111 |
127 |
151 |
162 |
161 |
138 |
132 |
139 |
140 |
118 |
114 |
141 |
150 |
157 |
161 |
100 |
190 |
171 |
173 |
160 |
163 |
160 |
178 |
191 |
181 |
183 |
194 |
177 |
165 |
172 |
169 |
179 |
167 |
189 |
169 |
174 |
180 |
136 |
131 |
113 |
117 |
163 |
159 |
136 |
131 |
113 |
156 |
160 |
164 |
112 |
119 |
155 |
142 |
129 |
110 |
176 |
184 |
193 |
158 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№29. Результаты измерения температуры раздела фракции бензин - авиакеросин на установке первичной переработке нефти ( в ° С.): |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
133 |
133 |
142 |
135 |
145 |
144 |
145 |
147 |
146 |
134 |
130 |
134 |
141 |
134 |
141 |
136 |
140 |
143 |
139 |
141 |
137 |
140 |
145 |
145 |
139 |
143 |
141 |
141 |
146 |
143 |
140 |
139 |
143 |
143 |
139 |
140 |
135 |
141 |
141 |
140 |
138 |
145 |
135 |
148 |
136 |
139 |
142 |
143 |
138 |
139 |
138 |
144 |
143 |
138 |
142 |
138 |
140 |
140 |
137 |
139 |
136 |
136 |
135 |
135 |
141 |
142 |
136 |
140 |
136 |
137 |
138 |
138 |
140 |
139 |
140 |
140 |
139 |
139 |
139 |
140 |
140 |
146 |
139 |
139 |
138 |
144 |
141 |
141 |
144 |
138 |
139 |
138 |
138 |
143 |
137 |
138 |
140 |
139 |
137 |
137 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№30. Получены значения толщины нефтенасыщенности пласта ( м ): |
|||||||||||
14,5 |
15,5 |
16,1 |
16,1 |
14,9 |
15,6 |
16,6 |
15,8 |
16,3 |
15,2 |
14,1 |
15,6 |
15,3 |
14,8 |
16,2 |
16,8 |
16 |
14,4 |
14,8 |
15,6 |
14,8 |
14,6 |
16,2 |
15,7 |
16,3 |
15,8 |
15,2 |
15,3 |
15,3 |
15,8 |
15,7 |
16,1 |
14,4 |
16,1 |
14,2 |
15,5 |
14,8 |
15,3 |
15,2 |
16,3 |
15,7 |
16,4 |
15,7 |
16,7 |
15,7 |
14,6 |
14,7 |
15 |
16,4 |
16,6 |
15,1 |
16,8 |
16,2 |
15,9 |
15,1 |
14 |
15,3 |
14,2 |
14,8 |
15,3 |
16,8 |
15,5 |
15,6 |
14,7 |
14,6 |
15,4 |
16 |
16,9 |
14,2 |
14 |
14,3 |
16,6 |
14 |
14,5 |
16,2 |
14,2 |
14,5 |
14,9 |
15,6 |
15,5 |
15,5 |
14,6 |
14,4 |
15,7 |
15,4 |
15,9 |
14,1 |
15,7 |
15,2 |
15,1 |
15,6 |
14,7 |
14,3 |
14,7 |
16,9 |
15,3 |
15,8 |
16 |
15,3 |
14,8 |
|
|
|
|
|
|
|
|