3. Сжатие распределения с ростом числа слагаемых

Закон больших чисел в форме Чебышева означает, что распределение случайной величины

сжимается с ростом n. Если математические ожидания одинаковы, т.е. M_i=a,то сжатие происходит в окрестности точкиa.

Аналитическииллюстрировать сжатие можно, если распределение для легко выписывается. Например, если _i распределены нормально N(a, ²), то случайная величина распределена по N(a, ²/n).Построим графики плотностей дляn =1, 4, 25, 100 и=1,a =1 (сделаем это в целях освоения пакета).

Статистическиубедиться в сжатии можно, наблюдая гистограммы при различных значенияхn(например, дляn =10, 40, 160, 640). Сгенерируем kраз (например, хотя бы k =20) случайную величину :и построим для этой выборки средних гистограммуH_n.Сравнивая гистограммы для различныхn, мы заметим сжатие (сделать самостоятельно).сжатие можно увидеть определением для каждогоn поминимального_min,максимального_max значений и размаха w = _{max - min .}

Выполнение:

a) графики плотностей:

б) Разброс средних

Образуем таблицу 20v 640cс наблюдениями, и для различныхn(10,40,160,640) определим средние, выделяя из таблицы первыеnстрок. Для полученных 4 строк найдем стандартное отклонение, минимум и максимум и транспонируем таблицу. Построим график.

Мы убедились, что с ростом nразброс уменьшается.

3. Усиленный закон больших чисел.

Эксперименты с монетой.

Из последовательности x₁ ,..., x_N независимых наблюдений построим последовательностьf₁, ..., f_Nсреднеарифметических, где

f_n =, n = 1, ..., N

и убедимся графически в том, что f_n cростомnприближается к математическому ожиданию.

Убеждаемся, что частота выпадения герба f_n cростомnприближается к вероятности гербар= 0,5.

Эксперименты со случайными числами, распределенными равномерно на отрезке [0, 1]. Наши действия аналогичны предыдущему. Убеждаемся, что последовательность среднеарифметических приближается к 0,5 – математическому ожиданию.

Убеждаемся, что последовательность среднеарифметических приближается к 0,5 – математическому ожиданию.

Пример невыполнения закона

Сгенерируем 3 выборки в первых трех столбцах таблицы, учитывая по (3), что tg(), если ~ R[0, 1],имеет распределение Коши.

Анализируя результирующие графики, видим, что кривые среднеарифметических иногда испытывают скачки, которые отбрасывают их значения далеко от 0 – центра распределения.

Задание

Промоделировать и посмотреть на графиках поведение средне-арифметического как функцию nдля случайных величин, распределенных с плотностью

p(x) = ,,

где a>0, c=1/(2a). Приa<1 математическое ожидание существует, но приa1 это не так. При увеличенииa (1, 1.5, 2, 5, 10) скачки в среднеарифметическом (как функцииn) будут увеличиваться. Генерацию случайных чисел можно сделать на формуле

,где u ~ R[0,1],

a  = 1с вероятностями 1/2.

изM (например,M =3) последовательностейx₁, x₂,...,x_n получить Mпоследовательностей средних₁,₂,...,_n, где

_k =,

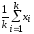можно так же, как и выше.

4. Теорема Гливенко основная теорема статистики

Пусть x₁, x₂,...,x_n - выборка изnнезависимых наблюдений над случайной величинойXс функцией распределенияF(x).Расположим наблюдения в порядке возрастания; получим

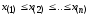
-вариационный ряд. Определим функцию эмпирического распределения

,

где - число тех наблюдений, для которыхx_i<x. Ясно, что- ступенчатая функция; это функция распределения, которое получается, если значениямx₁,...,x_n присвоить вероятности, равные1/n. Ясно, что-функция случайная , так.как зависит от наблюденийx₁,...,x_n.

Теорема Гливенко:

при

с вероятностью 1.

Проиллюстрируем эту теорему на примерах наблюдений над случайной величиной, распределенной по равномерному на [0,1] закону.

Задача

Сравним графически функцию эмпирического распределениядля выборки объемаn= 10 и функцию теоретического распределения. Будем работать в модулеData Management, поскольку операция сортировки находится в нем.

Решение

В первом столбце сгенерируем выборку объема 10 с равномерным на отрезке [0, 1] распределением. Построим вариационный ряд, т.е. сделаем сортировку по возрастанию. Во втором столбце вычислим значения функции эмпирического распределения. Поскольку функция равномерного на [a, b]распределения определяется на [a, b]отрезком прямой, ее можно задать двумя точками(а, 0)и(b, 1), в данном случае (0, 0) и (1, 1). Наблюдаем функции теоретического и эмпирического распределений:

Убеждаемся в том, что при увеличении nфункция эмпирического распределения приближается к теоретической.