Нелинейная зависимость

Связь между признаком x и yможет быть нелинейной, например, в виде полинома:

y = P_k (x) + ,

где P_k (x)=_о + ₁ x + ...+ _k x^k, k - степень полинома,- случайная составляющая, М = 0, D = ² .

Для имеющихся данных (x_i ,y_i),i= 1, ...,n, можно записать

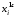y_i=_о + ₁ x_i + ₂ + ...+_k + _i , i =1, ...,n

или, как и (12), в матричной форме:

Y = X  +  ,

где .

Пример.Имеются эмпирические данные о зависимостиy- выработки на одного работника доменного производства отx- температуры дутья; данные приведены в табл. 3 в условных единицах.

Сначала оценим имеющиеся данные визуально, с помощью процедуры Scatterplot (диаграмма рассеяния):

Видим, что зависимость, возможно, нелинейная. Построим несколько регрессий.

1) Регрессия первой степени: y=_о + ₁ x (indep. Var.: x); получим (в скобках указаны стандартные ошибки оценок):

y= 5.37 + 1.40x

(0.98) (0.16)

= 0.795,s = 2.10.

2) Регрессия второй степени: y=_о + ₁ x + ₂ x² (indep. Var.: x, x2); получим:

y= 9.9 - 0.9x+ 0.21x², (31)

(1.33) (0.57) (0.05)

= 0.891,s= 1.53,

коэффициент ₁ = -0.9 незначимо отличается от 0. Эта регрессия лучше предыдущей в смыслеиs. Однако, возможно, регрессия третьей степени окажется лучше?

3) Построим регрессию третьей степени: y=_о + ₁ x + ₂ x² + ₃ x³

(indep. Var.: x, x2 , x3 ); получим:

y= 11.6 - 2.32х+ 0.52х²- 0.02х³

(2.33) (1.75) (0.36) (0.02)

= 0.890,s = 1.53,

незначимо отличаются от 0. Поскольку степень увеличилась без увеличения, от регрессии третьей степени отказываемся в пользу (31) второй степени. Однако, гипотеза о нулевом значении ₁ в (31) не отклоняется (p-level = 0.1), и потому построим

4) регрессию y=_о + ₂ x² без линейного члена (indep. Var.: x2 ); получим

y= 8.02 + 0.13x² (32)

(0.54) (0.01)

= 0.884,s= 1.6,

Сравнивая ее по иsс регрессией, включающей линейный член, отдаем предпочтение второй, поскольку ошибка прогнозаs меньше.

Обобщение нелинейной зависимости

Предполагается, что связь между факторами (х₁, ...,х_р) иyвыражается следующим образом:

y=_о + ₁ ₁ (х₁, ..., х_р)+ ₂  ₂ (х₁, ..., х_р)+ ... + _k  _k (х₁, ..., х_р) +

где _j ( ),j= 1, ...,k, - система некоторых функций. Имеетсяnнаблюдений при различных значенияхх(х₁, ..., х_р):x¹,x², ...,xⁿ ; имеем:

y_i = _o + ,i= 1, ...,n,

или в матричной форме:

y = X  +  ,

где Х- матрицаn(k+ 1), вi-й строке которой (1,₁ (xⁱ),₂ (xⁱ), ...,_k (xⁱ));

y,  , , как в ранее решенных задачах. Все формулы остаются справедливыми.

Построим регрессию для z₅. Рассмотрим полученные результаты:

По построенной регрессии:

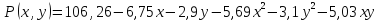
Ошибки оценок для коэффициентов можем наблюдать в столбце Std.Err.ofB.

Построим график полученной функции и найдем точку ее минимума:

По полученному графику можно судить, что точкой минимума является точка (-4;-4). В этой точке, следует заметить, нет конкретных измерений величиныz5. Среди всех точек, в которых такие измерения присутствуют, точкой минимума является точка (3,2);