НИУ МЭИ (МЭИ(ТУ))

Кафедра прикладной математики

Лабораторная работа №3 по дисциплине: «Математическая статистика»

на тему: «Сравнение оценок»

Выполнил:

студент группы А-13-08

Бочаров Иван

Москва, 2011

Решение конкретной задачи

Пример. Пусть на заводе имеется большая партия из N (тысячи) транзисторов, используемых для сборки некоторого прибора. Выходные параметры прибора (например, надежность, уровень шума, вероятность выхода из режима и т.д.) зависят от обратных токов транзисторов; обратный ток у разных экземпляров различен, и потому можно считать его случайной величиной, причем, как известно технологам, распределённой равномерно в диапазоне от 0 до I_max, где I_max— порог отбраковки, установленный на заводе - изготовителе транзисторов. Следовательно, выходные параметры прибора определяются величиной I_max. Предположим, что по каким-либо причинам значение I_max производителю приборов неизвестно. Ясно, что в этом случае из партии нужно случайным выбором извлечь n (сравнительно немного: десятки) транзисторов, измерить их ток, и по измерениям оценить I_max (неизвестный параметр а). Таким образом, возникает

Статистическая задача: по наблюдениям x₁, ..., x_n над случайной величиной C , распределённой равномерно на отрезке [0, a], оценить неизвестный параметр a.

сравним три способа оценивания (три оценки):

оценку, полученную методом моментов,

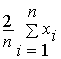a ₁ = ,                      (1)

оценку, полученную методом максимального правдоподобия (после исправления смещённости),

a ₂ = max x_i                  (2)

и оценку, полученную методом порядковых статистик,

a ₃ = 2 _0.5 = x_(k) + x_(k+1), (3)

где _0.5 = 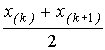— выборочная квантиль порядка 0.5, т.е. выборочная медиана; x_(k) — член вариационного ряда с номером k; здесь полагаем n = 2k. Точность этих оценок можно сравнить теоретически и экспериментально (статистически).

Теоретическое сравнение оценок

Все три оценки являются несмещенными.

Определим дисперсии оценок:

Da ₁ = D(  ) = ,

Da ₂ = D(max x_i ) = ,

Da ₃ = D(x_(k) + x_(k+1)) » ,

откуда ясно, что a ₂ — наиболее точная оценка, а a ₃ — наименее.

Поясним приведенные формулы для дисперсий.

Первая:

Da ₁ =  =  =  = .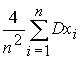

Вторая: определим функцию распределения статистики max x_i :

F(z) P{ max x_i < z} = P{x₁ < z, ..., x_n < z} =  = ;

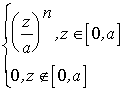Плотность распределения

p(z) = F? (z) = 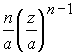, zI [0, a].

Далее

Ma ₂ = M( max x_i ) =  = ,

Ma ₂² = M=,

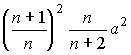Da ₂ = Ma ₂² — (Ma ₂)²=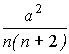 

ТретьяЖ используем теорему Крамера, согласно которой выборочная p -квантиль имеет дисперсию, равную приближенно 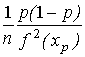 , где x_p — истинная p-квантиль, f(x) - плотность распределения наблюдений выборки. В нашем случае (при n = 2k) статистика

0.5 (x_(k) +x _(k+1) ) m

является выборочной медианой (p = 0.5) , f(x_0.5) = 1/a , a ₃ = 2m, и потому

Da ₃=Dm = =.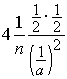

Статистическое сравнение оценок

Сформируем 20 выборок из равномерного на [0,10] распределения объема 10:

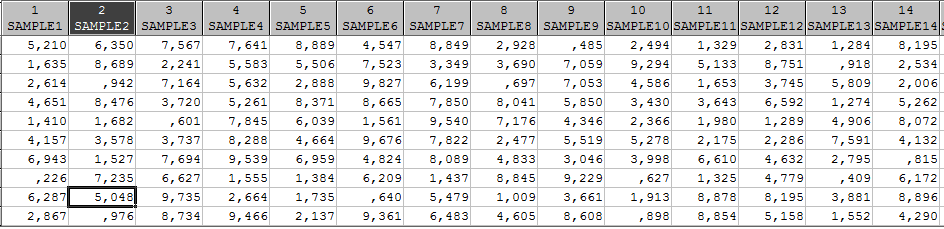
Вычислим необходимые для оценок статистики, а на их основе вычислим построенные оценки:

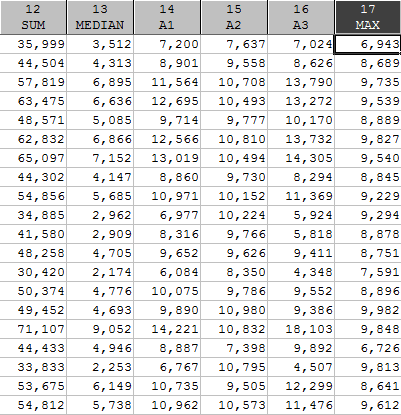
Вычислим характеристики оценок:

Приведем график, иллюстрирующий полученные результаты:

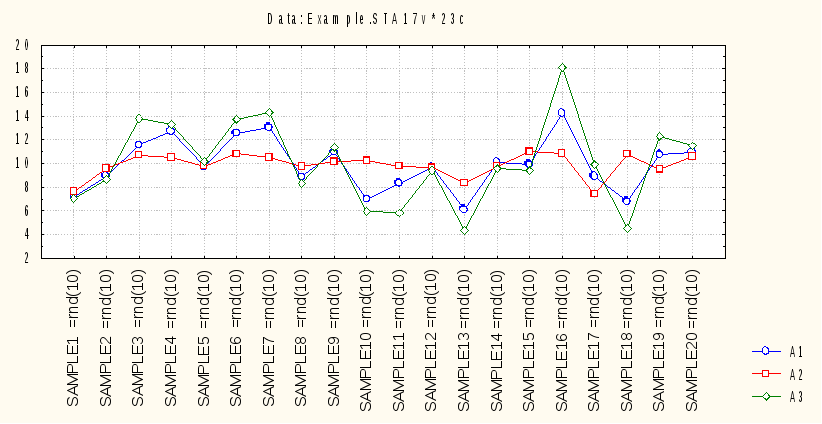
Запишем полученные данные в итоговую таблицу и проведем аналогичные манипуляции с выборками объема 40 и 160 с занесением данных в таблицу:

		A1	A2	A3
N=10	Amin	6.084	7.398	4.348
	Amax	14.221	10.980	18.103
	W	8.137	3.582	13.755
	Sa	2.236	1.021	3.578
N=40	Amin	8.490	10.208	7.149
	Amax	11.459	10.980	12.034
	W	2.969	0.772	4.885
	Sa	0.951	0.196	1.623
N=160	Amin	9.052	10.752	8.897
	Amax	10.767	10.998	11.133
	W	1.715	0.246	2.236
	Sa	0.453	0.063	0.615

Графически покажем уменьшение СКО с увеличением объема выборки:

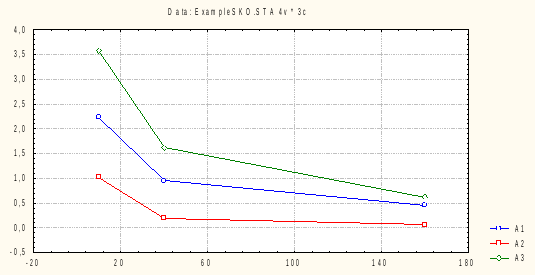
Сравнение значений размахов w и СКО S_а для 3 оценок показывает, что оценка a₂ (х₁, ... , х_n) наиболее точна, а оценка a₃ (х₁, ... , х_n) - наименее.

Приведенные результаты экспериментального сравнения 3 способов обработки наблюдений показывают следующее:

1. Значения оценок концентрируются в окрестности оцениваемого параметра (проявление свойства несмещенности оценок).

2. С ростом числа наблюдений точность (величина разброса) оценок улучшается (проявление свойства состоятельности).

3. Различные оценки различаются по величине средней ошибки, откуда ясно, что различные способы обработки наблюдений нужно сравнивать по величине среднего значения некоторого критерия качества, например, среднего значения квадрата ошибки.

Задание на самостоятельную работу

Сравним статистически на выборках объема n=10,40,160 две оценки: оценку максимального правдоподобия и медианную оценку

1) среднего нормального распределения и

2) параметра показательного распределения

Приведем заполненные итоговые таблицы:

Для среднего нормального распределения (m=3):

		A1	A2
N=10	Amin	1.994	2.046
	Amax	3.340	3.549
	W	1.346	1.503
	Sa	0.313	0.347
N=40	Amin	2.671	2.600
	Amax	3.189	3.463
	W	0.518	0.863
	Sa	0.144	0.232
N=160	Amin	2.861	2.788
	Amax	3.176	3.209
	W	0.315	0.421
	Sa	0.089	0.103

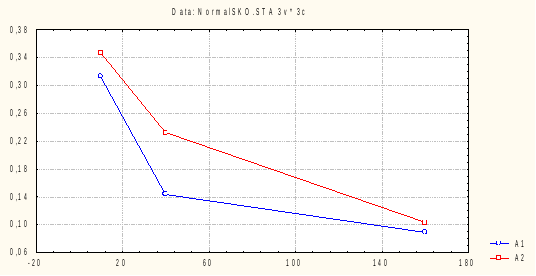
Для параметра показательного распределения (a=1):

		A1	A2
N=10	Amin	0.625	0.407
	Amax	1.926	1.725
	W	1.301	1.318
	Sa	0.324	0.375
N=40	Amin	0.643	0.668
	Amax	1.379	1.680
	W	0.736	1.012
	Sa	0.180	0.251
N=160	Amin	0.899	0.834
	Amax	1.116	1.285
	W	0.217	0.451
	Sa	0.051	0.130

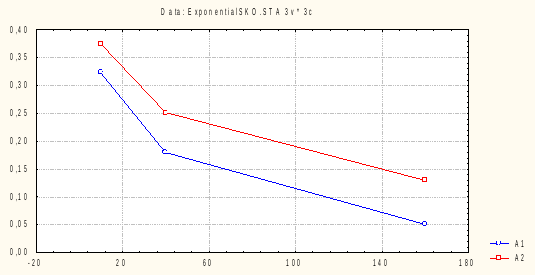
Сравнение значений размахов w и СКО S_а для 2 оценок показывает, что оценка a₁ (х₁, ... , х_n) более точна, чем оценка a₂ (х₁, ... , х_n).

Приведенные результаты экспериментального сравнения 3 способов обработки наблюдений показывают следующее:

1. Значения оценок концентрируются в окрестности оцениваемого параметра (проявление свойства несмещенности оценок).

2. С ростом числа наблюдений точность (величина разброса) оценок улучшается (проявление свойства состоятельности).