Лабораторные работы / Бочаров (5 вариант) / Лабораторная работа 1

Отчет

по лабораторной работе №1

по дисциплине:

«Математическая статистика»

Выполнил:

студент группы А-13-08

Бочаров Иван

Часть 1.  Теорема Бернулли

Образуем вектор длины 1850 при помощи средств пакета Statistica и заполним его значениями, вычисленными по формуле:

X = trunc (rnd (1) + 0,5)

Определим число появлений герба и относительную частоту в серии из 170 независимых испытаний. Число появлений герба равно 96, относительная частота появления герба равна 0.564706 . Очевидно, что |0.564706-0.5| < 0.1 .

Вычислим аналогичные величины для всех 1850 испытаний. Число появлений герба равно 967, относительная частота появления герба равна 0.522703 . Очевидно, что |0.522703-0.5| < 0.03 .

Часть 2. Закон больших чисел в форме Чебышева

Пример 1. Случайные величины распределены равномерно на отрезке [0,1]. Если значение e задавать произвольно, а число испытаний выбирать из условия n  (9Dx/ε²), то соотношение   из ЗБЧ в форме Чебышева выполняется с вероятностью P=0.997, а если n  (5.4Dx/ ε ²) - то с P=0.98.

Положим ε ₁ =0.1 и ε ₂ =0.02, определим два соответствующих значения n₁ =45 и n₂ =1125, и проверим соотношение экспериментально.

Вычислим среднее для первых 45 испытаний. Оно равно 0.468321 и отличается от 0.5 менее, чем на 0.1, что и требовалось продемонстрировать.

Проведем аналогичную операцию для 1125 испытаний. Среднее равно 0.503605 и отличается от 0.5 менее, чем на 0.03, что и требовалось продемонстрировать.

Задание 1. Проверить соотношение экспериментально для экспоненциально распределенных слагаемых с Mx =1. Принять ε₁ =0.2 и ε ₂ =0.05.

Знаем, что дисперсия экспоненциально распределенной случайной величины равна 1/a. В нашем случае Dx=1. Вычислим n1 и n2. Исходя из формулы, n1 = 225, а n2 = 3600.

Для заполнения вектора применим формулу:

X = VExpon(rnd(1);1)

Вычислим среднее для первых 225 испытаний. Оно равно 1.039169 и отличается от 1 менее, чем на 0.2, что и требовалось продемонстрировать.

Проведем аналогичную операцию для 3600 испытаний. Среднее равно 0.994853 и отличается от 1 менее, чем на 0.05, что и требовалось продемонстрировать.

Задание 2. Невыполнение закона больших чисел

Рассмотрим случайную величину, распределенную по закону Коши с плотностью . Покажем экспериментально, что закон больших чисел невыполним для случайной величины, распределенной этим образом.

Возьмем ε = 1 и сгенерируем 7 выборок из распределения Коши и проверим выполнение неравенства:  

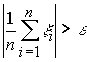
Убеждаемся, что в столбцах 2, 3 и 5 среднее превосходит единицу:

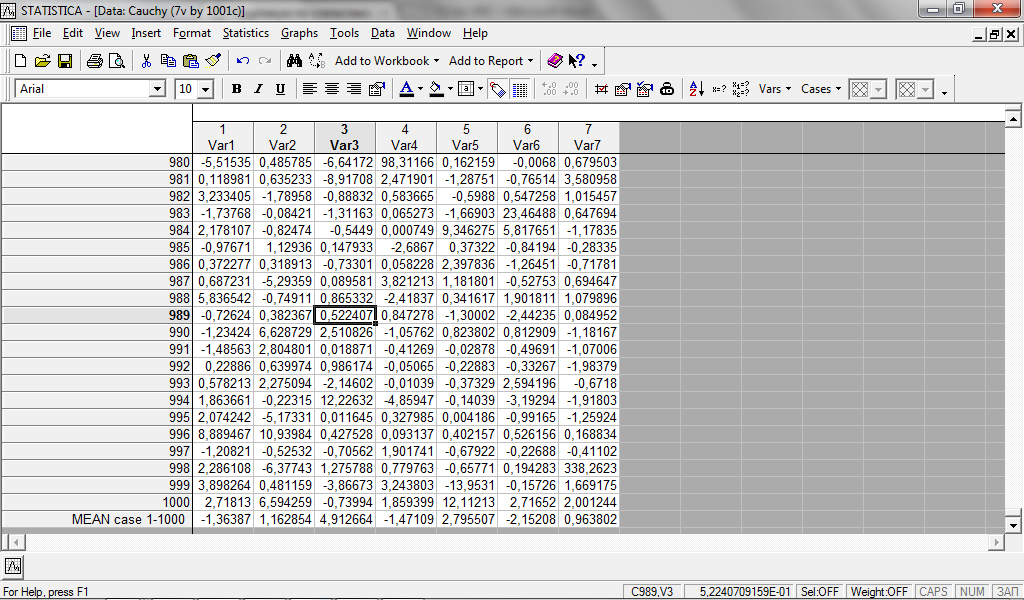
Построим график выборки 1 и обратим внимание на редкие наблюдения, далеко отстоящие от центра распределения:

Задание 3.

А) Сжатие распределения

Чтобы проиллюстрировать этот эффект, построим графики нормального распределения для σ=1, 0.5, 0.2,0.1

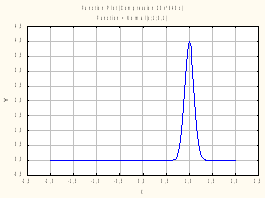
Б) Разброс средних

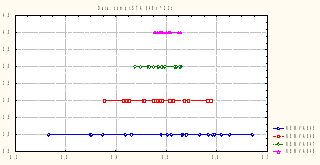
Сгенерируем 20 выборок длины 640 из равномерного распределения на [0;1]. По всем выборкам определим средние, а затем вычислим для них среднеквадратичное отклонение (для n=10, 40, 160, 640). Убеждаемся, что распределение сжимается (разброс средних уменьшается).

Покажем это графически:

Часть 3. Усиленный закон больших чисел

А) Бросание симметричной монеты

Сгенерируем 3 последовательности по 500 бросаний монеты в первые 3 столбца таблицы 6v x 500c; для удобства зададим имена переменным-столбцам: х₁, х₂, х₃, f₁, f₂, f₃. Образуем последовательность среднеарифметических, исходя из соотношений:

f₁ = x₁, f_n = ((n – 1) f_{n- 1} + x_n ) / n, n = 2, ..., N,

Посмотрим графически зависимость f_n от n в различных диапазонах: от 1 до 25, до 50, до 100, до 500:

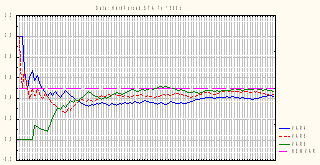
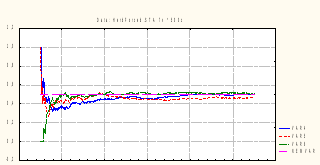
Проделаем аналогичную операцию для равномерно распределенных на отрезке [0;1] величин:

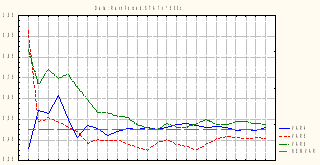
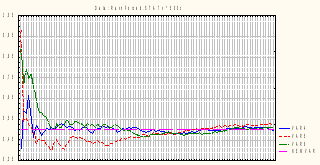
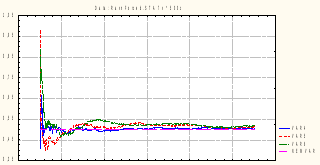
Пример невыполнения закона

Рассмотрим последовательности случайных чисел, распределенных по закону Коши.

Сгенерируем 3 выборки в первых трех столбцах таблицы, учитывая по (3), что tg (πx), если x ~ R [0, 1], имеет распределение Коши, выполним преобразования над первыми тремя столбцами; над первым:

= tan (var1* Pi)

и аналогично над остальными.

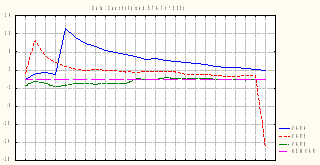
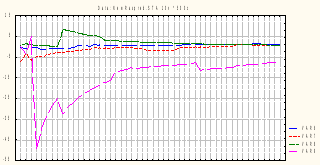
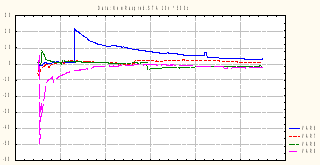
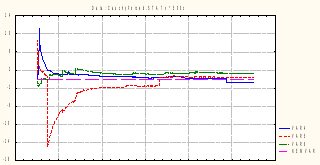Анализируя результирующие графики, видим, что кривые среднеарифметических иногда испытывают скачки, которые отбрасывают их значения далеко от 0 – центра распределения.

Задание 3

Промоделируем и посмотрим на графиках поведение средне-арифметического как функцию n для случайных величин, распределенных с плотностью

p(x) = 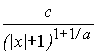 ,  , (9)

где a>0, c=1/(2a). При a<1 математическое ожидание существует, но при a1 это не так. При увеличении a (1, 1.5, 2, 5, 10) скачки в среднеарифметическом (как функции n) будут увеличиваться. Генерацию случайных чисел можно сделать на формуле

 , где u ~ R[0,1],

а ε = ± 1 с вероятностями 1/2.

Часть 4. Теорема Гливенко – основная теорема статистики

Теорема Гливенко:

 при 

с вероятностью 1.

Проиллюстрируем эту теорему на примерах наблюдений над случайной величиной, распределенной по равномерному на [0,1] закону.

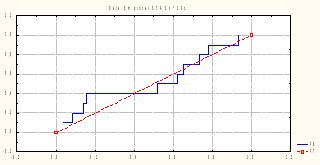
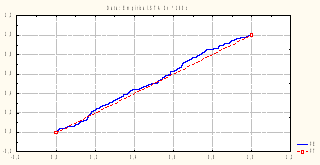
Сравним графически функцию эмпирического распределения для выборки объема n = 10 и функцию теоретического распределения. Будем работать в модуле Data Management, поскольку операция сортировки находится в нем.

Часть 5. Центральная предельная теорема

Задание 1.

Убедимся статистически, что сумма нескольких одинаково распределенных случайных величин распределена приближенно по нормальному закону.

Сделаем это на примере суммы

 (12)

шести (m = 6) независимых случайных величин, имеющих beta-распределение с параметрами a=b=0.5, плотность которого

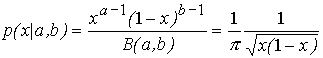 , (13)

где  - β-функция. Плотность при выбранных значениях параметров имеет U-образный вид, весьма далекий от нормального; убедимся в этом, построив график плотности .

Чтобы статистически оценить закон распределения для суммы S, следует многократно, N раз (например, N=500), промоделировать суммирование: получим S₁, S₂,...,S_N - выборку для суммы; для этой выборки построим гистограмму и сравним ее визуально с нормальной плотностью.

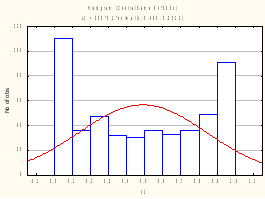
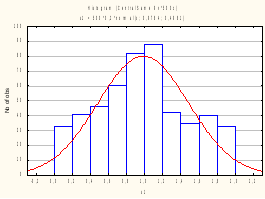
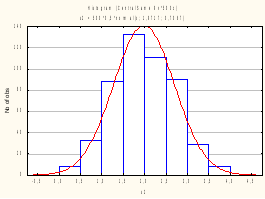
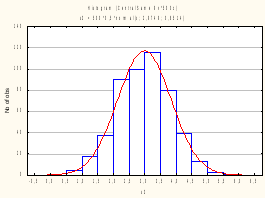
Получили гистограммы для одного, двух, четырех и шести слагаемых соответственно. Убедились, что сумма уже четырех слагаемых распределена близко к нормальному закону. Занесем значения статистики Колмогорова-Смирнова и уровня значимости в таблицу:

Число слагаемых	Статистика Колмогорова-Смирнова	Уровень значимости
1	0.10039	0.00000
2	0.04199	0.00000
4	0.03192	0.43289
6	0.03108	0.65917

Задание 2

Оценим экспериментально распределение для сумм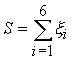ы  шести слагаемых, распределенных по различным законам; выберем их из семейства β-распределений (13), задав следующие параметры:

	1	2	3	4	5	6
a	1	0.5	2	1	2	1
b	0.5	1	1	2	2	1

Убедимся, что все плотности далеки от нормальной:  построим графики плотностей β - распределения с параметрами, указанными в таблице. Здесь приведем только один из них.

Сгенерировали выборку для суммы и построили гистограмму для нее. Убедились в том, что распределение близко к нормальному:

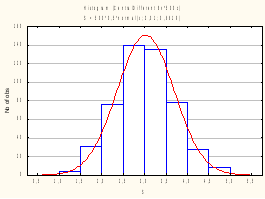
Приведем гистограмму одного из слагаемых:

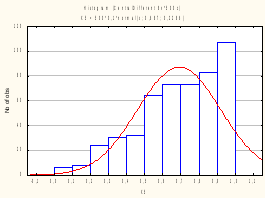
Распределение, как мы видим, далеко от нормального.

Если же в сумме имеется слагаемое, дисперсия которого существенно превышает все остальные, то приближенная нормальность места не имеет.

Проверим это (получим гистограмму), добавив в сумму 7-е слагаемое, имеющее β-распределение с параметрами a=b=0.5 и умноженное на 1000:

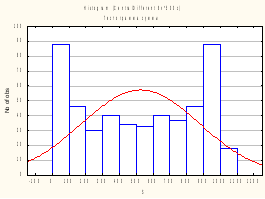
Убедились в невыполнении при вышеозначенных условиях.