
3. Методы статистических испытаний Монте-Карло.
Основная
идея методов Монте-Карло, применяемых
в задаче приближенного вычисления
неизвестной величины
![]() ,
заключается в следующем:
,
заключается в следующем:
-
подбирается случайная величина
 такая, что
такая, что
 и известен метод получения величины
и известен метод получения величины
 ;
; -
производится
 -кратное
получение величины
-кратное
получение величины
 ,
результатом которого является вектор
величин
,
результатом которого является вектор
величин
 ,
в котором все величины
,
в котором все величины
 имеют такое же распределение как и
величина
имеют такое же распределение как и
величина
 ;
; -
вычисляется величина
 ,
которая используется в качестве
приближенного значения
,
которая используется в качестве
приближенного значения
 .
.
Совокупность
случайных величин
![]() ,
…,
,
…,
![]() можно рассматривать как начальные
величины некоторой последовательности
можно рассматривать как начальные
величины некоторой последовательности
![]() ,
в которой все величины
,
в которой все величины
![]() имеют одинаковое распределение,
совпадающее с распределением
имеют одинаковое распределение,
совпадающее с распределением
![]() ,
откуда
,
откуда
![]() .
Если последовательность
.
Если последовательность
![]() удовлетворяет закону больших чисел,
тогда:
удовлетворяет закону больших чисел,
тогда:
![]() .
.
Отсюда
следует, что всегда можно подобрать
достаточно большое
![]() такое, что:
такое, что:
 ,
,
где
![]() и
и
![]() малые величины, то есть при достаточно
больших
малые величины, то есть при достаточно
больших
![]() величина
величина
![]() с большой вероятностью отклоняется от
с большой вероятностью отклоняется от
![]() лишь на малую величину не больше
лишь на малую величину не больше
![]() .
.
Вычисление
числа
![]() .
.
Пусть
в квадрате со стороной равной 1, размещена
четверть круга радиуса 1, и пусть
![]() и
и
![]() – независимые случайные величины,
имеющие равномерное распределение
– независимые случайные величины,
имеющие равномерное распределение
![]() .
Образуем бинарную случайную величину:
.
Образуем бинарную случайную величину:

которая
равна 4, если точка со случайными
координатами
![]() попадает внутрь круга, и равна 0 в
противном случае. Вычислим математическое
ожидание
попадает внутрь круга, и равна 0 в
противном случае. Вычислим математическое
ожидание
![]() :
:
 ,
,
где
![]() – совместная плотность вероятности
вектора
– совместная плотность вероятности
вектора
![]() .
Поскольку
.
Поскольку
![]() и
и
![]() независимы и имеют равномерное
распределение
независимы и имеют равномерное
распределение
![]() ,
то:
,
то:
![]() ,
,
тогда,
 .
.
Пусть
![]() ,
…,
,
…,
![]() –
–
![]() пар случайных величин, в которых все
величины попарно независимы и имеют
равномерное распределение
пар случайных величин, в которых все
величины попарно независимы и имеют
равномерное распределение
![]() .
Образуем совокупность величин
.
Образуем совокупность величин
![]() ,
…,
,
…,
![]() :
:
 ,
,
тогда на основании закона больших чисел:
![]() .
.
Определение характеристик сложных случайных величин.
Пусть
![]() – совокупность случайных величин с
плотностью вероятности
– совокупность случайных величин с
плотностью вероятности
![]() ,
для которой известен метод получения
реализаций,
,
для которой известен метод получения
реализаций,
![]() – некоторая известная функция и для
случайной величины
– некоторая известная функция и для
случайной величины
![]() требуется определить какие-либо
характеристики, например, значение
функции распределения в некоторой точке
или моменты.
требуется определить какие-либо
характеристики, например, значение
функции распределения в некоторой точке
или моменты.
Значение
функции распределения
![]() случайной величины
случайной величины
![]() в точке
в точке
![]() определяется интегралом:
определяется интегралом:
![]() ,
,
где
![]() – плотность вероятности вектора
– плотность вероятности вектора
![]() .
В общем случае, аналитическое вычисление
кратного интеграла по области
.
В общем случае, аналитическое вычисление
кратного интеграла по области
![]() может представлять определенные
трудности, поэтому для приближенного
вычисления используются методы
статистических испытаний.
может представлять определенные
трудности, поэтому для приближенного
вычисления используются методы
статистических испытаний.
На
основе случайного вектора
![]() образуем случайную величину:
образуем случайную величину:
 .
.
Легко
видеть, что математическое ожидание
![]() :
:
![]()
совпадает
с неизвестной величиной
![]() ,
подлежащей определению. Пусть
,
подлежащей определению. Пусть
![]() ,
…,
,
…,
![]() – совокупность независимых случайных
векторов, определим совокупность
случайных величин
– совокупность независимых случайных
векторов, определим совокупность
случайных величин
![]() ,
…,
,
…,
![]() ,
,

тогда:
![]() .
.
Заметим,
что величина
![]() совпадает с величиной эмпирической
функции распределения
совпадает с величиной эмпирической
функции распределения
![]() в точке
в точке
![]() (величины
(величины
![]() ).
).
Предположим,
требуется вычислить математическое
ожидание
![]() ,
где
,
где
![]() заданная функция (например,
заданная функция (например,
![]() ,
тогда
,
тогда
![]() – математическое ожидание
– математическое ожидание
![]() ,
или
,
или
![]() ,
тогда
,
тогда
![]() – дисперсия
– дисперсия
![]() ).
Определим случайную величину:
).
Определим случайную величину:
![]() ,
,
тогда
![]() .
Пусть
.
Пусть
![]() ,
…,
,
…,
![]() – совокупность независимых случайных
векторов, определим совокупность
случайных величин
– совокупность независимых случайных
векторов, определим совокупность
случайных величин
![]() ,
…,
,
…,
![]() :
:
![]() ,
,
тогда,
![]() .
.
Вычисление определенных интегралов.
Пусть
![]() – заданная функция, интегрируемая на
отрезке
– заданная функция, интегрируемая на
отрезке
![]() ,
где
,
где
![]() и
и
![]() конечные числа, и требуется приближенно
вычислить интеграл:
конечные числа, и требуется приближенно
вычислить интеграл:
![]() .
.
Задача вычисления интеграла с помощью методов статистических испытаний может быть решена двумя способами.
Первый
способ: предварительно преобразуем
интеграл с помощью замены переменных
![]() к виду:
к виду:
![]() ,
,
где
случайная величина
![]() имеет равномерное распределение
имеет равномерное распределение
![]() .
Пусть
.
Пусть
![]() ,
…,
,
…,
![]() – независимые случайные величины с
равномерным распределением
– независимые случайные величины с
равномерным распределением
![]() ,
определим величины
,
определим величины
![]() ,
…,
,
…,
![]() :
:
![]() ,
,
легко
видеть, что
![]() ,
тогда:
,
тогда:
![]() .
.
Второй
способ: поскольку
![]() интегрируема, то
интегрируема, то
![]() ограничена на отрезке
ограничена на отрезке
![]() ,
пусть
,
пусть
![]() при
при
![]() .
Преобразуем исходный интеграл к виду:
.
Преобразуем исходный интеграл к виду:
![]()
![]()
![]()
![]() ,
,
где
значения функции
![]() при
при
![]() .
Пусть
.
Пусть
![]() – случайный вектор, в котором
– случайный вектор, в котором
![]() и
и
![]() независимые случайные величины с
равномерным распределением
независимые случайные величины с
равномерным распределением
![]() ,
образуем случайную величину
,
образуем случайную величину
![]() :
:
![]() .
.
Заметим,
что математическое ожидание
![]() :
:
 .
.
Пусть
![]() ,
…,
,
…,
![]() –
–
![]() пар случайных векторов, в которых каждая
случайная величина не зависит от
остальных и имеет равномерное распределение
пар случайных векторов, в которых каждая
случайная величина не зависит от
остальных и имеет равномерное распределение
![]() .
Образуем случайные величины
.
Образуем случайные величины
![]() ,
…,
,
…,
![]() :
:
 ,
,
тогда,
![]() ,
,
![]() .
.
Вычисление несобственных интегралов.
Пусть
![]() – заданная функция, для которой сходится
интеграл,
– заданная функция, для которой сходится
интеграл,
![]() ,
,
и
требуется вычислить приближенно значение
![]() .
.
В
некоторых случаях удается ввести такую
функцию плотности вероятности
![]() ,
что:
,
что:
-
 ,
,
 ;
; -
сходится
 .
.
Тогда, как легко видеть,
![]() ,
,
поэтому
задача приближенного вычисления
![]() сводится к задаче приближенного
вычисления математического ожидания
сводится к задаче приближенного
вычисления математического ожидания
![]() ,
где случайная величина
,
где случайная величина
![]() имеет функцию плотности вероятности
имеет функцию плотности вероятности
![]() .
.
Для
приближенного вычисления математического
ожидания
![]() достаточно составить метод получения
независимых случайных величин
достаточно составить метод получения
независимых случайных величин
![]() ,
...,
,
...,
![]() ,
имеющих плотность вероятности
,
имеющих плотность вероятности
![]() ,
тогда:
,
тогда:
![]() .
.
Сравнение метода Монте-Карло и квадратурных методов.
Методы приближенного вычисления интегралов, представленные выше, допускают естественное обобщение на кратные интегралы, и как оказывается, при больших кратностях интегралов методы Монте-Карло имеют преимущество над квадратурными методами.
Квадратурные
методы используют значения подынтегральной
функции в узлах многомерной сетки,
поэтому объем вычислений производимых
квадратурными методами является
величиной порядка
![]() ,
где
,
где
![]() – кратность интеграла и
– кратность интеграла и
![]() – постоянная, характеризующая средние
вычислительные затраты на вычисление
функции в одном узле (и некоторые
усредненные затраты, связанные с
умножением на вес узла и сложением).
Методы Монте-Карло помимо вычисления
значения функции требуют вычисления
реализаций случайных величин (в частности
– постоянная, характеризующая средние
вычислительные затраты на вычисление
функции в одном узле (и некоторые
усредненные затраты, связанные с
умножением на вес узла и сложением).
Методы Монте-Карло помимо вычисления
значения функции требуют вычисления
реализаций случайных величин (в частности
![]() ),
поэтому постоянная, характеризующая
вычислительные затраты на одно вычисление
значения функции, оказывается больше
),
поэтому постоянная, характеризующая
вычислительные затраты на одно вычисление
значения функции, оказывается больше
![]() .
Тем не менее, при увеличении кратности
.
Тем не менее, при увеличении кратности
![]() увлечение количества суммируемых
величин
увлечение количества суммируемых
величин
![]() (увеличение
(увеличение
![]() происходит в силу требования достижения
заданной точности) линейно зависит от
происходит в силу требования достижения
заданной точности) линейно зависит от
![]() ,
поэтому в результате вычислительные
затраты в методах Монте-Карло являются
величиной порядка
,
поэтому в результате вычислительные
затраты в методах Монте-Карло являются
величиной порядка
![]() ,
то есть линейно зависят от
,
то есть линейно зависят от
![]() .
.
Экспериментальное
сравнение выявляет преимущество
квадратурных методов над методами
Монте-Карло при небольших кратностях
![]() порядка
порядка
![]() и
и
![]() ,
однако, при кратностях порядка 8 и больше
методы Монте-Карло имеют существенное
преимущество над квадратурными методами.
,
однако, при кратностях порядка 8 и больше
методы Монте-Карло имеют существенное
преимущество над квадратурными методами.
Точность методов Монте-Карло.
Пусть
в задаче приближенного вычисления
неизвестной величины
![]() по методу Монте-Карло со случайной
величиной
по методу Монте-Карло со случайной
величиной
![]() (
(![]() и вектором независимых случайных величин
и вектором независимых случайных величин
![]() ставится дополнительное условие о том,
что вычисленное значение должно
отличаться от
ставится дополнительное условие о том,
что вычисленное значение должно
отличаться от
![]() на малую величину
на малую величину
![]() с вероятностью не меньше заданной
с вероятностью не меньше заданной
![]() (близкой к 1). Каким образом следует
выбирать число
(близкой к 1). Каким образом следует
выбирать число
![]() суммируемых величин для удовлетворения
дополнительного условия?
суммируемых величин для удовлетворения
дополнительного условия?
Формально дополнительное условие имеет вид:
 .
.
Для
оценки количества
![]() требуется вычислить вероятность в левой
части неравенства, и для вычисления в
некоторых случаях допустимо использовать
независимость величин
требуется вычислить вероятность в левой
части неравенства, и для вычисления в
некоторых случаях допустимо использовать
независимость величин
![]() и асимптотическую нормальность суммы:
и асимптотическую нормальность суммы:
![]() при
при
![]() ,
,
где
 ,
,
 .
.
Таким образом,


 ,
,
Откуда,
 ,
,
 ,
,
 ,
,
|
|
(10.4) |
Если
дисперсия
![]() может быть вычислена аналитически,
тогда из (10.4) можно определить число
может быть вычислена аналитически,
тогда из (10.4) можно определить число
![]() .
Если же дисперсию
.
Если же дисперсию
![]() не удается вычислить аналитически, то
допустимо использовать верхнюю оценку
не удается вычислить аналитически, то
допустимо использовать верхнюю оценку
![]() ,
,
![]() ,
вместо дисперсии
,
вместо дисперсии
![]() в (10.4). В некоторых случаях в (10.4) вместо
дисперсии
в (10.4). В некоторых случаях в (10.4) вместо
дисперсии
![]() используют выборочную дисперсию:
используют выборочную дисперсию:
![]() ,
,
где
![]() .
.
Из соотношения (10.4) следует:
а)
количество требуемых испытаний
![]() прямо пропорционально дисперсии
прямо пропорционально дисперсии
![]() ,
поэтому следует стараться выбрать
величину
,
поэтому следует стараться выбрать
величину
![]() таким образом, чтобы дисперсия
таким образом, чтобы дисперсия
![]() оказалась как можно меньше (при условии,
что
оказалась как можно меньше (при условии,
что
![]() ).
).
б)
при увеличении точности в 10 раз (![]() )
требуемое количество слагаемых
)
требуемое количество слагаемых
![]() возрастает в 100 раз.
возрастает в 100 раз.
|
|
|

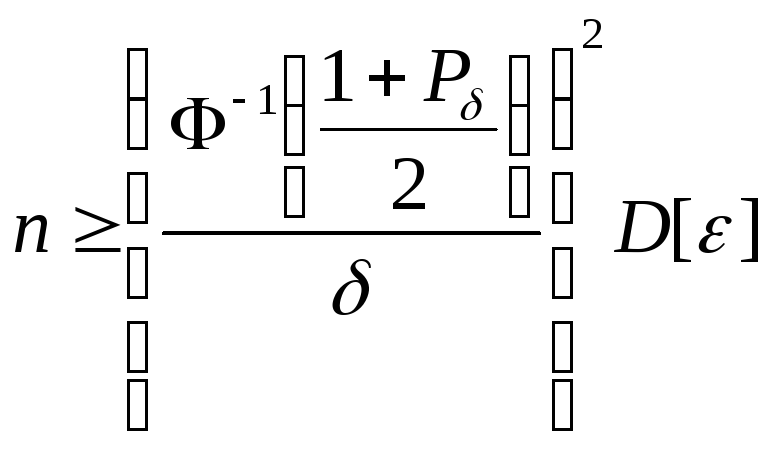 .
.