4. Точечное оценивание старших моментов для функции распределения.

При построении оценок начальных и центральных моментов и():

,

,

используются статистики аналогичные введенным ранее статистикам (2.2) и (2.3):

,	(2.5)
,	(2.6)
.

Определение 2.5.

Статистика называетсявыборочным моментом -го порядка.

Определение 2.6.

Статистика называетсявыборочным центральным моментом -го порядка.

Легко видеть, что статистики являются несмещенными оценками, действительно:

.

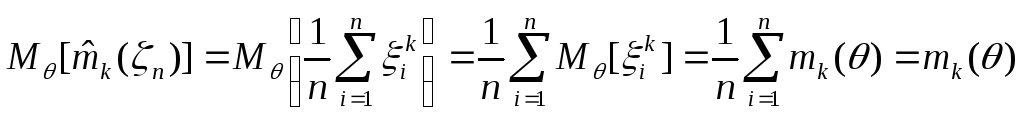Кроме того, если существует момент , то дисперсия статистики:

,

поскольку при в силу независимостии,

.

Таким образом,

.

Поскольку существует, то существует и, и с ростом, очевидно, дисперсиястремиться к нулю. Тогда в силу утверждения 2.1 (ранее было показано, что оценкаявляется несмещенной) оценкаявляется состоятельной.

Кроме того, можно показать ([1], параграф 1.3), что статистики являются асимптотически нормальными.

Исследование свойства несмещенности оценок сопряжено с определенными трудностями, тем не менее, достаточно легко убедиться в состоятельности оценок. Заметим, что статистикивыражаются через статистики, где:

.

Таким образом, статистики являются непрерывными функциями от состоятельных оценок, которые сходятся по вероятности к значениям, отсюда в силу свойства сходимости по вероятности статистикасходится по вероятности к:

, при.

Заметим, что справа от предела стоит в точности :

Таким образом, статистика сходится по вероятности к:

, при,

отсюда статистика является состоятельной (по определению).

5. Линейная оценка среднего с минимальной дисперсией при разноточных измерениях.

Известно, что случайные величины () имеют вид:

,

где неизвестное числовое значение,попарно независимые случайные величины с математическим ожиданиеми дисперсией, значенияизвестны. Требуется построить оценкунеизвестной величины, такую что

1) Оценка линейная:

,

2) Оценка является несмещенной оценкой:

3) Оценка имеет наименьшую дисперсию в классе линейных оценок:

.

Легко видеть, что , тогда:

.

Поскольку должна быть несмещенной оценкой, то нужно потребовать чтобы:

.

.

Вычислим дисперсию , учитывая, что в силу попарной независимости величинковариацияпри:

.

Таким образом, приходим к задаче минимизации квадратичной формы по неизвестнымпри условии, что. Для решения задачи нахождения условного экстремума воспользуемся методом множителей Лагранжа, функция Лагранжаимеет вид:

.

Дифференцируя по и, получим систему:

.

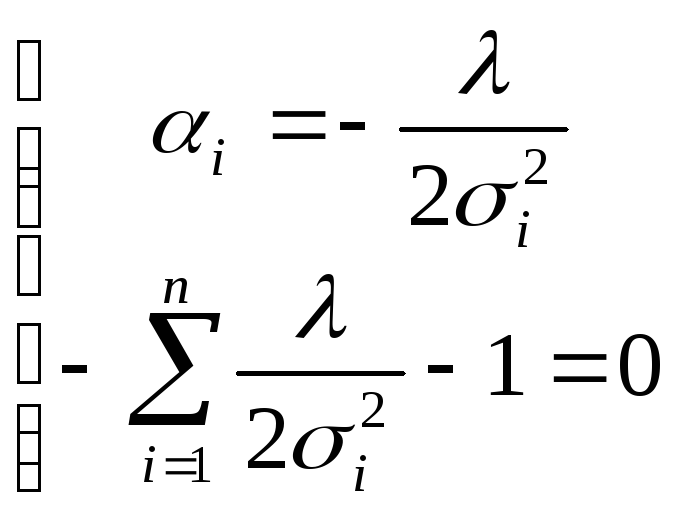
Таким образом, искомая оценка имеет вид:

,

при этом дисперсия оценки :

.

Обозначим , тогдаи отсюда становится понятно, что чем меньше, тем больше коэффициент, то есть чем более «точным» является измерение, тем с большим «весом» оно входит в сумму оценки. Например, если-ое измерение «точнее»-го в 3 раза, то есть, тогда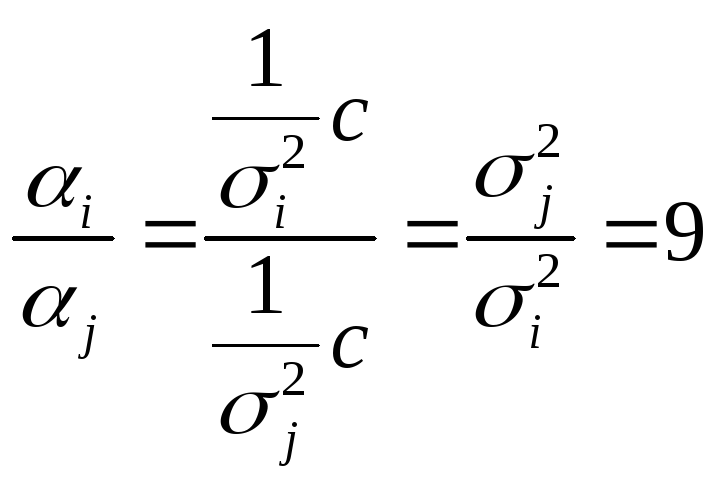, то есть «вес» измеренияв сумме оценкивраз больше «веса» измерения.

23