Тема 3. Неравенство Рао-Крамера, эффективные оценки. Информация Фишера. Достаточные статистики.

1. Нижняя граница дисперсии несмещенной оценки. Неравенство Рао-Крамера.

Ранее указывалось, что оценки можно сравнивать на основе дисперсий – из двух оценок «лучше» та оценка, дисперсия которой меньше. Вполне естественно, что наибольший интерес представляют оценки с наименьшей возможной дисперсией и отсюда возникает ряд вопросов и в частности насколько малой может быть дисперсия оценки из некоторого класса (в частности из класса несмещенных оценок). Для несмещенных оценок ответ на этот вопрос в некоторых случаях дает неравенство Рао-Крамера: при выполнении условий регулярности дисперсия несмещенной оценки не может быть меньше некоторой вполне определенной величины.

Определение 3.1.

Пусть – вектор случайных величин ифункция плотности вероятности (или вероятность) вектора. Функциярассматриваемая как функция параметрапри фиксированных, ...,называетсяфункцией правдоподобия.

Определение 3.2.

Пусть – вектор случайных величин и– функция правдоподобия. Случайная функция

называется функцией вклада.

Определение 3.3.

Пусть – вектор случайных величин и– функция вклада. Функция

называется информацией Фишера о параметре , содержащейся в наблюдении.

В том случае, когда наблюдение представляет собой выборкуиз распределенияс плотностью вероятности:

,

все случайные величины выборки () имеют функцию распределения, поэтому функцияявляется плотностью вероятности для каждой из случайной величины выборки(). Поскольку случайные величины выборки, …,независимы, то плотность вероятностивекторной случайной величины:

.

Таким образом, если наблюдение является выборкой, то функция правдоподобия:

,

при этом функция вклада может быть записана следующим образом:

.

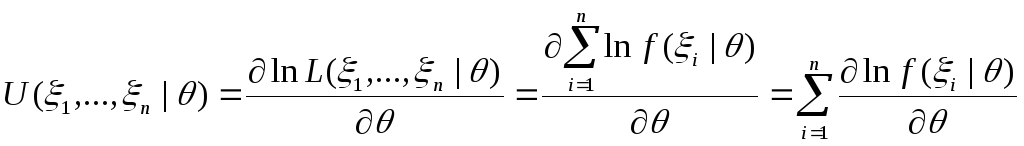Пусть – множество всех возможных значений случайного вектораи– множество всех допустимых значений параметра, далее будем считать, что выполнены следующие условия, которые назовемусловиями регулярности:

R1) Множество не зависит от параметра.

R2) На множестве функция правдоподобияположительна:

при всех .

R3) Функция правдоподобия дифференцируема по параметрупри всехи всех.

R4) При всех справедливо равенство:

.

R5) При всех существует момент:

Заметим, что при каждом значении функция правдоподобияявляется функцией плотности вероятности, поэтому, как и для всякой другой функции плотности вероятности, для функциисправедливо равенство:

.

Продифференцируем левую и правую часть по и, пользуясь условиями регулярностиR1, R3 и R4, внесем дифференцирование под знак интеграла:

В силу условия R2 преобразуем подынтегральную функцию:

.

Таким образом,

(3.1)

Заметим, что слева от знака равенства стоит в точности , таким образом, при выполнении условий регулярности:

.

Отсюда информацию Фишера при выполнении условий регулярности можно представить следующим образом:

.

Теперь перейдем к рассмотрению основного результата, касающегося дисперсий несмещенных оценок, который дается следующей теоремой.

Теорема 3.4. (неравенство Рао-Крамера)

Пусть наблюдение представляет собой вектор случайных величин ,– функция правдоподобия вектора, параметр, где– непустое множество допустимых значений параметра,– оценка величины. Если,

1) статистика является несмещенной оценкой величины;

2) функция дифференцируема попри всех;

3) выполнены условия регулярности R1-R5;

4) при всех существует производная:

;

тогда

,

где информация Фишера о параметре, содержащаяся в наблюдении.

Доказательство:

1) По условию 1 статистика является несмещенной оценкой:

.

Продифференцируем левую и правую часть по (производная левой части существует в силу условия 2, в правой – в силу условия 4) и в правой части внесем дифференцирование под знак интеграла (в силу условия 4):

Преобразуем правую часть в силу условия R2 (также как при выводе 3.1):

(3.2)

2) При выполнении условий регулярности справедливо соотношение (3.1):

Умножим левую и правую часть на и внесем в правой частикак множитель, не зависящий от переменных интегрирования, …,:

(3.3)

3) Из (3.2) вычитаем (3.3):

.

По условию 1 теоремы статистика является несмещенной оценкой:

.

В условиях регулярности (условие 3 теоремы) математическое ожидание функции вклада равно нулю (соотношение 3.1):

.

Таким образом:

.

В соответствии со свойством ковариации:

.

Таким образом,

.

Отсюда,

,

поскольку по определению информация Фишера .

Теорема доказана.

Следствие 3.5.

В условиях теоремы 3.4 равенство

имеет место тогда и только тогда, когда оценка и функция вкладасвязаны линейно, причем:

,

где .

Доказательство:

1) Пусть выполнено равенство , тогда

,

поскольку по определению . В пункте 3 доказательства теоремы 3.4 было показано, что

,

тогда

.

Отсюда по свойству ковариации следует, что оценка и функция вкладасвязаны линейной зависимостью:

(3.4)

Вычисляя математическое ожидание левой и правой частей (3.4), получим:

.

В условиях теоремы 3.4 справедливы условия регулярности, при выполнении которых , тогда:

.

Статистика является несмещенной, то есть, тогда:

.

Вычисляя дисперсию левой и правой части (3.4), получим:

.

Поскольку по определению , тои поскольку выполнено равенство, то. Таким образом,

,

где .

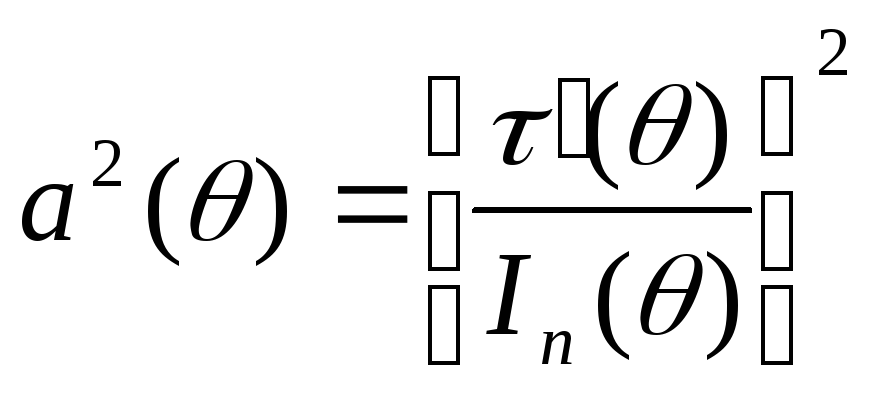2) Пусть статистика и функция вкладасвязаны линейной зависимостью:

,

тогда по свойству ковариации:

.

В пункте 3 доказательства теоремы 3.4 было показано, что

,

отсюда,

,

тогда,

,

так как по определению .

Поскольку статистика и функция вкладасвязаны линейно и выполнено равенство, то, как и в пункте доказательства 1, вычисляя математическое ожидание и дисперсию левой и правой части соотношения:

,

можно показать, что и.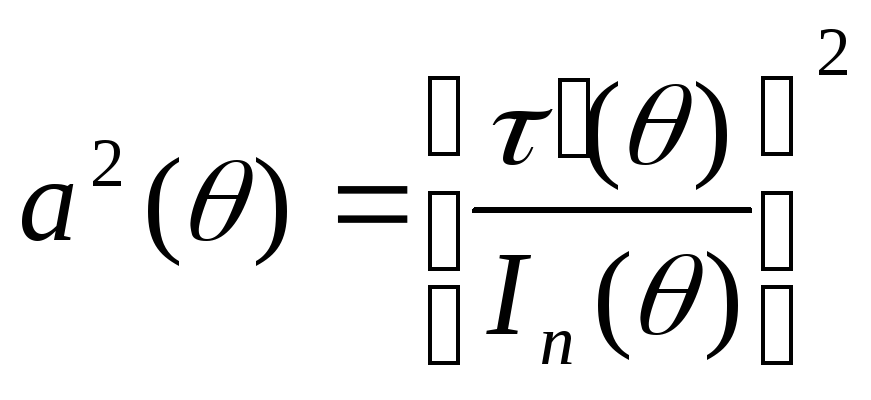

Следствие доказано.

Замечание

В многомерном случае неравенство Рао-Крамера формулируется следующим образом: пусть – вектор случайных величин,– многомерный параметр,,, …,– несмещенные оценки,, …,, тогда при некоторых условиях:

,

(3.5)

где – дисперсионная матрица случайных величин,, …,(),– информационная матрица Фишера (),– матрица производных (), символозначает транспонирование. Неравенство (3.5) следует понимать в следующем смысле: для любого вектора-столбца,

.

Выражение, стоящее слева, есть квадратичная форма , а выражение, стоящее справа, – квадратичная форма:

.

Преобразуем выражение, стоящее слева, обозначив вектор-столбец случайных величин и вектор-столбец функций:

.

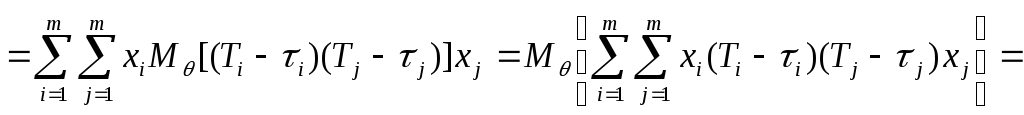
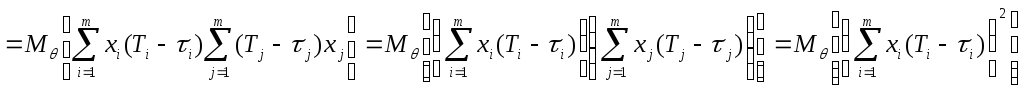Поскольку , …,несмещенные оценки, …,, то, тогда,

.

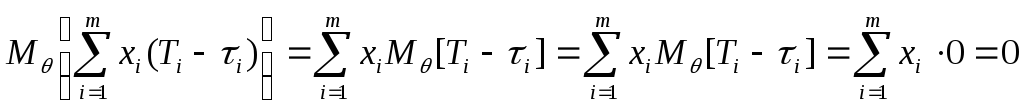Таким образом,

,

поскольку 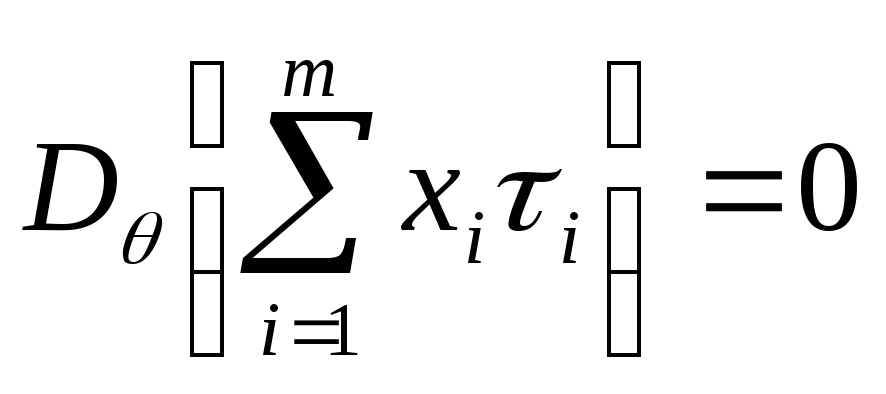, так как– не случайная величина, тогда,

.

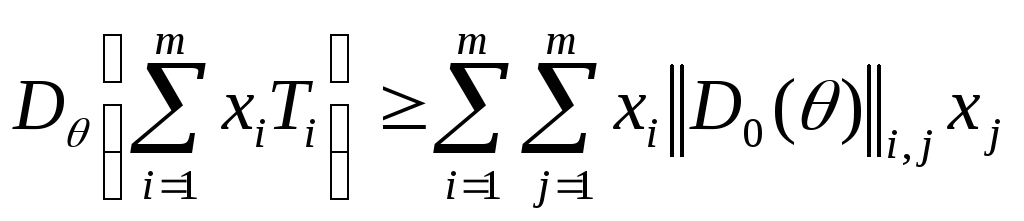Выберем произвольным образом ,, и представим, что в векторе-ая компонента равна единице, а все остальные компоненты равны нулю:

,

тогда левая часть неравенства окажется равной , а правая – соответствующему диагональному элементу:

,

Отсюда следует, что диагональные элементы матрицы являются нижними границами дисперсий оценок, …,.