
3. Метод порядковых статистик.
Утверждение 4.8.
Пусть
![]() – выборка из распределения
– выборка из распределения
![]() ,
тогда функция распределения
,
тогда функция распределения
![]() -ой
порядковой статистики
-ой
порядковой статистики
![]() :
:

Доказательство:
Выберем произвольным образом и зафиксируем
значение
![]() ,
определим на основе выборки
,
определим на основе выборки
![]() вектор бинарных случайных величин
вектор бинарных случайных величин
![]() :
:
 .
.
Случайные величины
![]() независимы в совокупности (поскольку
случайные величины
независимы в совокупности (поскольку
случайные величины
![]() независимы в совокупности) и имеют
одинаковое распределение
независимы в совокупности) и имеют
одинаковое распределение
![]() (поскольку случайные величины
(поскольку случайные величины
![]() имеют одинаковую функцию распределения)
:
имеют одинаковую функцию распределения)
:
![]() ,
,
![]() .
.
Пусть
![]() –
–
![]() -ая
порядковая статистика, по определению
функция распределения
-ая
порядковая статистика, по определению
функция распределения
![]() :
:
![]() .
.
Порядковая статистика
![]() меньше величины
меньше величины
![]() тогда и только тогда, когда среди величин
выборки
тогда и только тогда, когда среди величин
выборки
![]()
![]() (
(![]() )
величин меньше
)
величин меньше
![]() и
и
![]() величин не меньше
величин не меньше
![]() ,
то есть тогда и только тогда, когда в
векторе бинарных случайных величин
,
то есть тогда и только тогда, когда в
векторе бинарных случайных величин
![]()
![]() величин равны 1 и
величин равны 1 и
![]() величин равны 0, что эквивалентно тому,
что случайная величина
величин равны 0, что эквивалентно тому,
что случайная величина
![]() больше или равна
больше или равна
![]() .
Поскольку все
.
Поскольку все
![]() независимы и одинаково распределены,
то случайная величина
независимы и одинаково распределены,
то случайная величина
![]() имеет распределение Бернулли с параметрами
имеет распределение Бернулли с параметрами
![]() и
и
![]() ,
тогда:
,
тогда:
|
|
(4.13) |
Заметим, что полученное равенство
справедливо для любого
![]() ,
поскольку величина
,
поскольку величина
![]() была выбрана произвольным образом.
была выбрана произвольным образом.
При
![]() из (4.13) получим:
из (4.13) получим:
![]()
![]()
![]() .
.
При
![]() из (4.13) получим:
из (4.13) получим:
![]() .
.
Утверждение доказано.
Утверждение 4.9
Пусть выполнены условия утверждения
4.8 и функция распределения
![]() дифференцируема при всех
дифференцируема при всех
![]() и
и
![]() ,
тогда плотность вероятности
,
тогда плотность вероятности
![]() -ой
порядковой статистики
-ой
порядковой статистики
![]() :
:
![]() ,
,
где
![]() – плотность вероятности.
– плотность вероятности.
Доказательство:
Действительно, для того, чтобы получить
выражение для плотности вероятности
![]() достаточно продифференцировать функцию
распределения
достаточно продифференцировать функцию
распределения
![]() :
:
При
![]() получим:
получим:
![]() .
.
При
![]() получим:
получим:
![]() .
.
При
![]() получим (для краткости опускаем аргумент
функций):
получим (для краткости опускаем аргумент
функций):

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Утверждение доказано.
Порядковые статистики используются для построения оценок квантилей распределений и параметров.
Определение 4.10.
Пусть
![]() – функция распределения,
– функция распределения,
![]() -квантиль
(квантиль уровня
-квантиль
(квантиль уровня
![]() )
функции распределения
)
функции распределения
![]() есть число
есть число
![]() такое, что:
такое, что:
![]() .
.
(если существует несколько значений
![]() ,
удовлетворяющих условию
,
удовлетворяющих условию
![]() ,
то в качестве
,
то в качестве
![]() -квантили
принимают наименьшее из этих значений).
-квантили
принимают наименьшее из этих значений).
Если распределение, соответствующее
![]() имеет название, то обычно говорят,
например, «квантиль уровня
имеет название, то обычно говорят,
например, «квантиль уровня
![]() нормального распределения с параметрами
0 и 1» или «квантиль уровня
нормального распределения с параметрами
0 и 1» или «квантиль уровня
![]() распределения хи-квадрат с
распределения хи-квадрат с
![]() степенями свободы».
степенями свободы».
Предположим, что функция распределения
![]() зависит от неизвестного параметра
зависит от неизвестного параметра
![]() ,
тогда
,
тогда
![]() -квантиль
является функцией параметра
-квантиль
является функцией параметра
![]() и является неизвестной величиной. Для
построения оценки
и является неизвестной величиной. Для
построения оценки
![]() -квантили
-квантили
![]() функцию распределения
функцию распределения
![]() заменяют эмпирической функцией
распределения
заменяют эмпирической функцией
распределения
![]() .
.
Определение 4.11.
Пусть
![]() – эмпирическая функция распределения
выборки
– эмпирическая функция распределения
выборки
![]() и
и
![]() – реализация выборки
– реализация выборки
![]() ,
число
,
число
![]() называется выборочной
называется выборочной
![]() -квантилью,
если:
-квантилью,
если:
![]() .
.
Поскольку реализации эмпирической
функции распределения являются
кусочно-постоянными функциями, то для
![]() (где
(где
![]() – целое число,
– целое число,
![]() )
существует бесконечно много значений
)
существует бесконечно много значений
![]() ,
удовлетворяющих условию
,
удовлетворяющих условию
![]() ,
а для
,
а для
![]() ,
вообще говоря, нет ни одного значения
,
вообще говоря, нет ни одного значения
![]() ,
удовлетворяющего условию
,
удовлетворяющего условию
![]() .
В таком случае в качестве оценки
.
В таком случае в качестве оценки
![]() -квантили
-квантили
![]() используют порядковую статистику
используют порядковую статистику
![]() «наиболее близкую» к выборочной
«наиболее близкую» к выборочной
![]() -квантили
-квантили
![]() ,
для этого, как нетрудно убедиться,
достаточно положить
,
для этого, как нетрудно убедиться,
достаточно положить
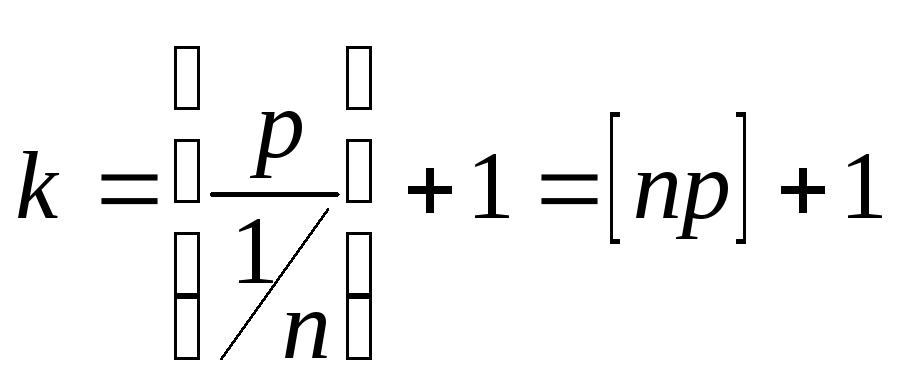 (где
(где
![]() – целая часть числа). Таким образом, в
качестве оценки
– целая часть числа). Таким образом, в
качестве оценки
![]()
![]() -квантили
следует взять величину:
-квантили
следует взять величину:
![]() .
.
Теорема 4.12. (Крамер)
Пусть
![]() – выборка из распределения
– выборка из распределения
![]() ,
,
![]() –
–
![]() -квантиль
распределения
-квантиль
распределения
![]() и в некоторой окрестности точки
и в некоторой окрестности точки
![]() плотность вероятности
плотность вероятности
![]() непрерывно дифференцируема и положительна,
непрерывно дифференцируема и положительна,
![]() ,
тогда статистика
,
тогда статистика
![]() имеет асимптотически нормальное
распределение:
имеет асимптотически нормальное
распределение:
 ,
при
,
при
![]() .
.
Следствие
При выполнении условий теоремы 4.12
статистика
![]() является состоятельной оценкой
является состоятельной оценкой
![]() -квантиля
-квантиля
![]() ,
поскольку математическое ожидание
,
поскольку математическое ожидание
![]() и дисперсия
и дисперсия
![]() при
при
![]() .
.
Пусть функция распределения
![]() зависит от неизвестного параметра
зависит от неизвестного параметра
![]() ,
для построения оценки величины
,
для построения оценки величины
![]() с помощью порядковых статистик достаточно
выразить величину
с помощью порядковых статистик достаточно
выразить величину
![]() через квантили функции распределения
через квантили функции распределения
![]() :
:
![]() .
.
Использование вместо квантилей
![]() ,
…,
,
…,
![]() их оценок, полученных с помощью порядковых
статистик,
их оценок, полученных с помощью порядковых
статистик,
![]() ,
…,
,
…,
![]() ,
приводит к статистике:
,
приводит к статистике:
![]() ,
,
которая используется в качестве оценки
![]() .
.
При некоторых условиях статистики
![]() являются состоятельными оценками
квантилей
являются состоятельными оценками
квантилей
![]() ,
то есть имеет место сходимость по
вероятности
,
то есть имеет место сходимость по
вероятности
![]() при
при
![]() ,
если функция
,
если функция
![]() непрерывна в точке
непрерывна в точке
![]() ,
тогда по свойству сходимости по
вероятности статистика
,
тогда по свойству сходимости по
вероятности статистика
![]() сходится по вероятности к величине
сходится по вероятности к величине
![]() :
:
![]() ,
при
,
при
![]() ,
,
тогда по определению статистика
![]() является состоятельной оценкой
является состоятельной оценкой
![]() .
.
Оценки, полученные методом порядковых статистик, как правило, имеют дисперсию больше, чем дисперсии оценок, полученные другими методами. Тем не менее, оценки, полученные методом порядковых статистик, могут обладать дополнительными положительными свойствами, например, устойчивостью к «засорению» выборки («засорение» выборки означает наличие в выборке ошибочных значений, полученных в результате неверного измерения и т.п.)
|
|
|

