Тема 4. Методы построения оценок.

1. Метод моментов.

Пусть – выборка из распределения , где – вектор неизвестных параметров, и требуется построить оценку величин , , …, .

Для построения оценок вычислим моментов () функции распределения , в общем случае моменты могут быть как начальные, так и центральные и не обязательно по порядку. Выражения для моментов содержат неизвестные параметры , …, , так что каждый момент представляет собой функцию :

.

Пусть представленная система разрешима относительно неизвестных параметров , …, , тогда получим систему выражений:

Точные значения моментов неизвестны, но известны оценки моментов , полученные на основе выборки . Используя оценки , получим оценки неизвестных параметров:

(4.1)

Определение 4.1.

Оценки , …, в системе (4.1) называются оценками, полученными по методу моментов (кратко, моментными оценками).

Моментные оценки , …, в общем случае не обладают свойством несмещенности (тем не менее, в некоторых частных случаях моментные оценки оказываются несмещенными).

Если функция () непрерывна в точке , то моментная оценка является состоятельной. Действительно, оценки начальных и центральных моментов являются состоятельными, откуда в силу свойства сходимости по вероятности, непрерывная функция от оценок , имеющих пределом по вероятности , сходится по вероятности к величине , таким образом:

,

что означает состоятельность оценоки .

Если в качестве используются первые начальных моментов функции распределения , функции , …, непрерывно дифференцируемы и функция распределения имеет моментов, то моментные оценки имеют асимптотически нормальное распределение:

,

где – вектор начальных моментов.

Моментные оценки в большом количестве случаев не являются эффективными и оптимальными, тем не менее, метод построения оценок оказывается простым и сами выражения для моментных оценок (4.1), как правило, оказываются простыми для вычисления.

2. Метод максимального правдоподобия.

Пусть – наблюдение (не обязательно выборка) и – плотность вероятности (или вероятность в дискретном случае) вектора , которая зависит от неизвестного вектора параметров . В результате проведения эксперимента будет получен числовой вектор , подставляя который в функцию , получим функцию, зависящую только от вектора (функцию правдоподобия – определение 3.1). При одних значениях параметра значение функции правдоподобия оказывается мало, при других значениях – велико. Поскольку значение функция правдоподобия отражает вероятность получения заданного вектора , то волне естественно выбрать параметр так, чтобы вероятность получения наблюдаемого значения оказалось бы наибольшей.

Определение 4.2.

Пусть – наблюдение и – функция правдоподобия. Оценка , доставляющая наибольшее значение функции правдоподобия при каждом наблюдении , называется оценкой максимального правдоподобия (кратко, МП-оценкой):

.

Определение 4.2 следует понимать в следующем смысле: при каждом фиксированном элементарном событии , случайные величины наблюдения , …, принимают определенные числовые значения , а само наблюдение при фиксированном становится числовым вектором . Для заданного вектора согласно определению 4.2 вычисляется значение МП-оценки :

.

Тем самым для каждого задан способ вычисления МП-оценки , который и определяет функцию наблюдения . Таким образом, МП-оценка как функция наблюдения является статистикой.

Если при каждой реализации вектора наибольшее значение функции правдоподобия соответствует внутренней точке множества допустимых значений параметра и функция правдоподобия дифференцируема по параметру, то из необходимого условия экстремума следует равенство частных производных функции правдоподобия нулю в точке МП-оценки :

, .

Решение приведенной системы не всегда оказывается удобным, поэтому при выполнении определенных условий задачу нахождения наибольшего значения функции правдоподобия заменяют задачей нахождения наибольшего значения логарифма функции правдоподобия , поскольку логарифм функция монотонно возрастающая (и, следовательно, наибольшему значению логарифма функции правдоподобия будет соответствовать наибольшее значение самой функции правдоподобия):

, .

В случае скалярного параметра представленное уравнение имеет название уравнения правдоподобия.

Утверждение 4.3.

Пусть выполнены условия теоремы 3.4, – наблюдение и статистика является эффективной оценкой параметра , тогда является МП-оценкой параметра .

Доказательство:

Поскольку – эффективная оценка и выполнены условия теоремы 3.4, то в силу следствия 3.5 имеет место равенство:

,

.

Пусть – МП-оценка, тогда при всех реализациях вектора :

,

отсюда при всех реализациях векторах :

,

тогда при всех реализациях вектора :

,

.

Таким образом, оценки и совпадают.

Утверждение доказано.

Утверждение 4.4.

Пусть – наблюдение и – статистика достаточная для параметра , тогда МП-оценка параметра является функцией достаточной статистики .

Доказательство:

Поскольку – достаточная для параметра статистика, то по критерию факторизации (теорема 3.12) для функции правдоподобия имеется разложение:

В соответствии с определением МП-оценка доставляет наибольшее значение функции правдоподобия :

.

Значение параметра , соответствующее наибольшему значению функции , будет зависеть от , …, только через значения статистики , поэтому МП-оценка будет функцией статистики :

.

Утверждение доказано.

Определение 4.5.

Статистика , являющаяся оценкой неизвестного параметра , называется асимптотически эффективной, если при каждом допустимом значении :

,

где – дисперсия оценки , – нижняя граница дисперсии из неравенства Рао-Крамера, – информация Фишера о параметре , содержащаяся в наблюдении .

Определение 4.6.

Статистика называется асимптотически нормальной с параметрами и :

при ,

если при каждом :

,

где – функция распределения , – функция Лапласа (функция распределения нормальной случайной величины с математическим ожиданием 0 и дисперсией 1).

Теорема 4.7. (асимптотические свойства МП-оценок)

Пусть – выборка из распределения с плотностью вероятностью , зависящей от скалярного параметра , – множество допустимых значений параметра, – истинное значение параметра, – МП-оценка параметра .

Если,

1) при каждом и почти всех существуют производные , и ;

2) при каждом и почти всех : и , причем существуют интегралы и ;

3) при каждом и почти всех : и существует единая постоянная такая, что для всех : .

4) при каждом конечен и положителен интеграл:

Тогда,

1) МП-оценка состоятельна, то есть при ;

2) МП-оценка является асимптотически нормальной;

3) МП-оценка асимптотически эффективная;

Доказательство:

1) Пусть – функция правдоподобия выборки , поскольку – выборка из распределения с плотностью вероятности , то в силу независимости и одинаковости распределений случайных величин () для функции правдоподобия получим выражение:

,

откуда,

(4.2)

Разложим функцию в точке истинного значения параметра :

,

где – некоторая точка между и . Поскольку по условию , то , где , тогда:

Подставляя разложение в (4.2), получим:

.

Разделим левую и правую части на :

(4.3)

Вычислим математическое ожидание случайных величин :

,

где дифференцирование по параметру можно вынести за интеграл в силу условий 1) и 2) теоремы. Поскольку случайные величины независимы и имеют одинаковое распределение, то таковыми же являются случайные величины и поскольку математические ожидания случайных величин:

,

то к этим случайным величинам применима теорема Хинчина, согласно которой имеет место сходимость по вероятности:

при

(4.4)

Вычислим математическое ожидание случайных величин :

,

где – информация Фишера, содержащаяся в наблюдении, состоящем из одной случайной величины . Случайные величины независимы и имеют одинаковое распределение, поскольку случайные величины , …, образуют выборку. Математические ожидания случайных величин существуют и все равны , отсюда по теореме Хинчина имеет место сходимость по вероятности:

при

(4.5)

Случайные величины () независимы и имеют одинаковое распределение, поскольку случайные величины , …, образуют выборку, математическое ожидание , согласно условию 4 теоремы. Отсюда, к случайным величинам применима теорема Хинчина, поэтому имеет место сходимость по вероятности:

при

(4.6)

Выберем произвольным образом и зафиксируем числа и , представим соотношение (4.3) в следующем виде:

(4.7)

где , и .

Согласно (4.4) сходится по вероятности к нулю, поэтому найдется такое, что при каждом:

,

Пусть событие , тогда .

Согласно (4.5) сходится по вероятности к , поэтому найдется такое, что при каждом :

,

Легко видеть, что событие, стоящее справа можно представить как объединение двух событий:

.

Пусть , тогда , откуда

.

Согласно (4.6) сходится по вероятности к , поэтому найдется такое, что при каждом :

,

,

.

Пусть , легко видеть, что

,

то есть событие , тогда

.

Пусть и заключается в том, что выполнены все три неравенства, тогда дополнительное событие состоит из тех элементарных событий , при которых не выполнено хотя бы одно неравенство. Поскольку все элементарные события , при которых выполнено неравенство , заключены во множестве , то . Аналогично, и , тогда:

и следовательно,

,

тогда,

При справедливы неравенства:

,

,

,

причем согласно условию 4 теоремы:

,

тогда, при :

, , .

(4.8)

Выберем произвольным образом и зафиксируем , рассмотрим -окрестность точки , пусть , тогда из (4.7):

Поскольку выполнены неравенства (4.8) и , то

.

Легко видеть, что и , причем если , то:

,

то есть при положительное слагаемое больше, чем модуль отрицательного слагаемого , тогда, очевидно,

.

Пусть теперь , тогда из (4.7) получим:

Поскольку выполнены неравенства (4.8) и , то:

Очевидно, что и , а при как и ранее , то есть модуль отрицательного слагаемого больше положительного слагаемого , откуда следует, что:

.

Таким образом, при в -окрестности функция , как функция параметра , принимает как положительные так и отрицательные значения. Поскольку существует производная , то функция , как функция параметра , является непрерывной, тогда из (4.2) функция так же непрерывна, как сумма непрерывных функций. По известной теореме анализа, для непрерывной функции , принимающей в -окрестности как положительные так и отрицательные значения найдется точка в которой функция принимает значение ноль:

,

причем сама точка находится внутри -окрестности точки , .

Таким образом, для всякого и достаточно малого существует решение уравнения правдоподобия – точка , причем такое, что , причем .

Заметим, что есть множество только некоторых таких , при которых существует решение уравнения правдоподобия и , возможно есть и другие такие , не входящие во множество . Пусть теперь – множество всех , при которых существует решение уравнения правдоподобия при заданном и , тогда, очевидно, и следовательно .

Итого, для произвольного и достаточно малого произвольного найдется число такое, что для каждого множество всех элементарных событий , при которых существует решение уравнения правдоподобия , такое что , имеет вероятность больше, чем :

,

отсюда по определению сходимости по вероятности МП-оценка сходится по вероятности к и по определению состоятельности МП-оценка является состоятельной.

2) Пусть – МП-оценка параметра , тогда является решением уравнения правдоподобия:

.

Отсюда с учетом (4.3):

,

где и , тогда:

,

,

,

,

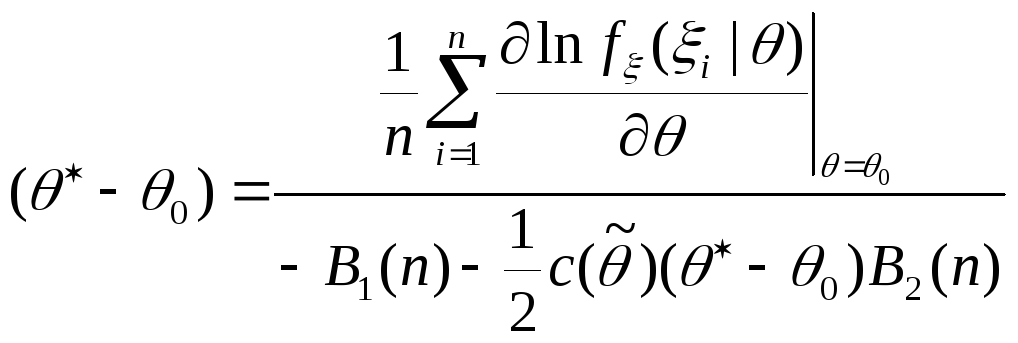(4.9)

Поскольку случайные величины , …, образуют выборку, то они совместно независимы и имеют одинаковую функцию распределения, отсюда следует, что случайные величины так же совместно независимы и имеют одинаковую функцию распределения, причем как было показано ранее . Заметим, что , отсюда в силу совместной независимости :

.

Таким образом, числитель правой части (4.9) можно представить в виде:

(4.10)

Случайные величины совместно независимы, имеют одинаковое распределение, конечное математическое ожидание 0 и конечную дисперсию (условие 4 теоремы), поэтому к ним применима центральная предельная теорема, согласно которой правая часть (4.10) имеет асимптотически нормальное распределение с параметрами 0 и , и следовательно числитель правой части (4.9):

, при .

В знаменателе правой части (4.9) случайная величина сходится по вероятности к (соотношение (4.5)), поэтому по свойству сходимости по вероятности случайная величина сходится по вероятности к 1:

, при

(4.11а)

Случайная величина сходится по вероятности к (соотношение (4.6)), МП-оценка состоятельна (согласно пункту 1 доказательства), поэтому сходится по вероятности к , следовательно разность сходится по вероятности к 0, тогда по свойству сходимости по вероятности произведение сходится по вероятности к . Постоянная конечна, поэтому по свойству сходимости по вероятности произведение сходится по вероятности к :

, при

(4.11б)

Из (4.11а) и (4.11б) следует сходимость по вероятности знаменателя правой части (4.9) к 1:

, при .

Таким образом, числитель правой части (4.9) имеет асимптотически нормальное распределение с параметрами 0 и 1, а знаменатель сходится по вероятности к 1, по свойству сходимости по вероятности правая часть (4.9) имеет асимптотически нормальное распределение с параметрами 0 и 1, тогда и левая часть (4.9) имеет асимптотически нормальное распределение с параметрами 0 и 1:

, при .

Отсюда следует, что имеет асимптотически нормальное распределение с параметрами и :

, при

(4.12)

3) Поскольку , …, образуют выборку, то информация Фишера о параметре , содержащейся в выборке , согласно утверждению 3.8:

.

Поскольку оценивается сам параметр , то в неравенстве Рао-Крамера , тогда и, следовательно, нижняя граница дисперсии в неравенстве Рао-Крамера:

.

Поскольку в пунктах 1 и 2 доказательства не накладывалось никаких ограничений на , то каким бы ни оказалось истинное значение параметра имеет место асимптотическая нормальность МП-оценки , то есть при любом значении параметра из (4.12) получим:

, при .

Отсюда следует, что дисперсия МП-оценки стремиться к при :

,

то есть МП-оценка оценка по определению асимптотически эффективная.

Теорема доказана.