
3. Критерий хи-квадрат проверки сложной гипотезы о вероятностях.
Пусть проводится серия из
![]() независимых испытаний, в каждом из
которых может произойти в точности одно
из событий
независимых испытаний, в каждом из
которых может произойти в точности одно
из событий![]() ,
…,
,
…,![]() ,
имеющих неизвестные вероятности
,
имеющих неизвестные вероятности![]() ,
…,
,
…,![]() .
По результатам серии фиксируются
количества наступлений событий
.
По результатам серии фиксируются
количества наступлений событий![]() ,
…,
,
…,![]() ,
так что наблюдение представляет собой
вектор случайных величин
,
так что наблюдение представляет собой
вектор случайных величин![]() ,
имеющий полиномиальное распределение
,
имеющий полиномиальное распределение![]() .
.
Основная гипотеза
![]() заключается в том, что неизвестные
вероятности
заключается в том, что неизвестные
вероятности![]() равны заданным выражениям
равны заданным выражениям![]() при некотором значении параметра
при некотором значении параметра![]() (в общем случае параметр
(в общем случае параметр![]() является
является![]() -мерным):
-мерным):
![]() :
:![]() ,
…,
,
…,![]() .
.
Требуется предложить статистический
критерий проверки гипотезы
![]() .
.
Заметим, что сформулированная задача,
схожа с задачей, рассмотренной в пункте
2, отличие заключается в том, что
гипотетические вероятности
![]() являются не числовыми значениями, а
некоторыми функциями параметра
являются не числовыми значениями, а
некоторыми функциями параметра![]() .
Указанное отличие не позволяет в качестве
статистики критерия использовать
статистику
.
Указанное отличие не позволяет в качестве
статистики критерия использовать
статистику![]() :
:
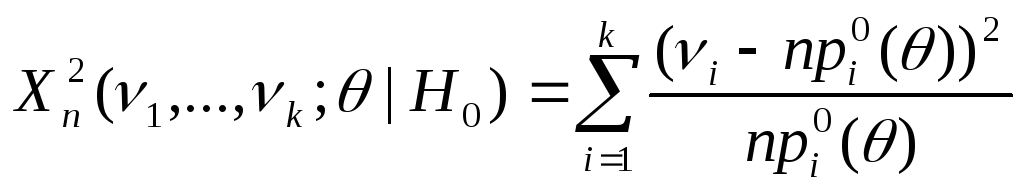 ,
,
поскольку статистика
![]() оказывается зависимой от параметра
оказывается зависимой от параметра![]() ,
теорема Пирсона (6.15)
не может быть применима и как следствие
предельное (при
,
теорема Пирсона (6.15)
не может быть применима и как следствие
предельное (при![]() )
распределение статистики
)
распределение статистики![]() неизвестно. Более того, следует ожидать,
что это распределение окажется различным
при различных значениях параметра
неизвестно. Более того, следует ожидать,
что это распределение окажется различным
при различных значениях параметра![]() .
Тем не менее, при специальном выборе
параметра
.
Тем не менее, при специальном выборе
параметра![]() удается найти предельное распределение.
удается найти предельное распределение.
Предположим, что при каждой реализации
наблюдения
![]() значение параметра
значение параметра![]() выбирается таким образом, чтобы
минимизировать значение статистики
выбирается таким образом, чтобы
минимизировать значение статистики![]() .
Минимальные значения статистики
.
Минимальные значения статистики![]() образуют новую статистику
образуют новую статистику![]() ,
не зависящую от параметра:
,
не зависящую от параметра:
 .
.
Пусть
![]() – значение параметра
– значение параметра![]() ,
при котором достигается минимальное
значение статистики
,
при котором достигается минимальное
значение статистики![]() ,
тогда:
,
тогда:

Теорема 6.18.(Фишер)
Пусть наблюдение
![]() имеет полиномиальное распределение
имеет полиномиальное распределение![]() и основная гипотеза
и основная гипотеза![]() заключается в том, что:
заключается в том, что:
![]() :
:![]() ,
,
где
![]() –
–![]() -мерный
параметр и
-мерный
параметр и![]() – известные функции. Если гипотеза
– известные функции. Если гипотеза![]() верна, тогда распределение статистики:
верна, тогда распределение статистики:
 ,
,
стремиться при
![]() к распределению
к распределению![]() .
.
Без доказательства.
Вычисление статистики
![]() требует трудоемкой операции нахождения
минимума, а для решения в общем виде
требует нахождения функции
требует трудоемкой операции нахождения
минимума, а для решения в общем виде
требует нахождения функции![]() доставляющей минимум статистики
доставляющей минимум статистики![]() ,
что существенно затрудняет использование
статистического критерия. Оказывается,
сформулированная выше теорема Фишера
справедлива и в том случае, когда вместо
функции
,
что существенно затрудняет использование
статистического критерия. Оказывается,
сформулированная выше теорема Фишера
справедлива и в том случае, когда вместо
функции![]() используется МП-оценка
используется МП-оценка![]() параметра
параметра![]() ,
вычисляемая по функции правдоподобия,
составленной в соответствии с тем видом
функции распределения наблюдения,
которую определяет гипотеза
,
вычисляемая по функции правдоподобия,
составленной в соответствии с тем видом
функции распределения наблюдения,
которую определяет гипотеза
![]() .
.
Теорема 6.19.(Фишер)
Пусть наблюдение
![]() имеет полиномиальное распределение
имеет полиномиальное распределение![]() и основная гипотеза
и основная гипотеза![]() заключается в том, что:
заключается в том, что:
![]() :
:![]() ,
,
где
![]() –
–![]() -мерный
параметр (
-мерный
параметр (![]() – множество допустимых значений
параметра
– множество допустимых значений
параметра![]() ),
и функции
),
и функции![]() таковы, что:
таковы, что:
1)
![]() (
(![]() ),
),
2) существуют и непрерывны производные
![]() (
(![]() ,
,![]() ),
),
3) существуют и непрерывны производные
![]() (
(![]() ,
,![]() ,
,![]() ),
),
4) для всех
![]() ранг матрицы, образованной частными
производными,
ранг матрицы, образованной частными
производными,![]() равен
равен![]() .
.
Если гипотеза
![]() верна и
верна и![]() – МП-оценка параметра
– МП-оценка параметра![]() ,
тогда распределение статистики,
,
тогда распределение статистики,

стремится при
![]() к распределению
к распределению![]() .
.
Без доказательства.
В качестве критической области
![]() выбирается область вида:
выбирается область вида:
![]() ,
,
где пороговое значение
![]() выбирается исходя из заданного уровня
значимости
выбирается исходя из заданного уровня
значимости![]() как квантиль уровня
как квантиль уровня![]() распределения
распределения![]() .
В остальном статистический критерий
аналогичен статистическому критерию
хи-квадрат, рассмотренному в пункте 2.
.
В остальном статистический критерий
аналогичен статистическому критерию
хи-квадрат, рассмотренному в пункте 2.
Проверка гипотезы о распределении с неизвестным параметром.
Пусть
![]() – выборка из неизвестного распределения
– выборка из неизвестного распределения![]() и основная гипотеза
и основная гипотеза![]() заключается в том, что
заключается в том, что![]() ,
где
,
где![]() – функция распределения известная с
точностью до значения параметра
– функция распределения известная с
точностью до значения параметра![]() .
Требуется предложить критерий проверки
гипотезы
.
Требуется предложить критерий проверки
гипотезы![]() .
.
На практике сформулированную задачу
заменяют другой, но «близкой» задачей:
выбираются точки
![]() и рассматривается разбиение числовой
оси на полуинтервалы и интервалы:
и рассматривается разбиение числовой
оси на полуинтервалы и интервалы:
![]() ,
,![]() ,
…,
,
…,![]() .
.
Рассматриваются события
![]() ,
…,
,
…,![]() :
:
![]() .
.
Легко видеть, что,
![]() ,
,
![]() ,
,
…,
![]() .
.
Для исходной выборки
![]() определяется вектор
определяется вектор![]() так, что:
так, что:
![]() ,
,
 .
.
В качестве основной гипотезы рассматривается
«расширенная» гипотеза
![]() :
:
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
…,
![]() .
.
Для проверки гипотезы
![]() используется статистический критерий
со статистикой
используется статистический критерий
со статистикой![]() ,
где
,
где![]() – МП-оценка параметра
– МП-оценка параметра![]() .
.
В качестве критической области
![]() выбирается область вида:
выбирается область вида:
![]() ,
,
где
![]() – квантиль уровня
– квантиль уровня![]() распределения
распределения![]() и
и![]() – заданный уровень значимости.
– заданный уровень значимости.
На практике, как правило, сперва
вычисляется МП-оценка
![]() ,
и лишь затем производится разбиение
числовой оси с помощью точек
,
и лишь затем производится разбиение
числовой оси с помощью точек![]() ,
…,
,
…,![]() так чтобы
так чтобы![]() .
.
Проверка гипотезы о независимости признаков.
Пусть проводится серия из
![]() независимых испытаний, в каждом из
которых происходит в точности одно из
событий
независимых испытаний, в каждом из
которых происходит в точности одно из
событий![]() ,
…,
,
…,![]() и в точности одно из событий
и в точности одно из событий![]() ,
…,
,
…,![]() ,
причем вероятности совместного
наступления событий
,
причем вероятности совместного
наступления событий![]() неизвестны. По результатам серии
фиксируется количество
неизвестны. По результатам серии
фиксируется количество![]() наступлений каждой пары
наступлений каждой пары![]() ,
таким образом наблюдение
,
таким образом наблюдение![]() имеет полиномиальное распределение
имеет полиномиальное распределение![]() .
.
Основная гипотеза
![]() заключается в том, что события
заключается в том, что события![]() и
и![]() попарно независимы, то есть вероятности
попарно независимы, то есть вероятности![]() ,
или иначе неизвестные вероятности
,
или иначе неизвестные вероятности![]() при некоторых числах
при некоторых числах![]() и
и![]() ,
где вектор вероятностей
,
где вектор вероятностей![]() играет роль параметра:
играет роль параметра:
![]() :
:![]() ,
,
![]() ,
,![]() .
.
Заметим, что
![]() и
и![]() ,
поэтому эти вероятности не входят в
вектор параметров
,
поэтому эти вероятности не входят в
вектор параметров![]() .
Требуется предложить статистический
критерий проверки гипотезы
.
Требуется предложить статистический
критерий проверки гипотезы![]() .
.
Для решения задачи используется критерий хи-квадрат проверки сложной гипотезы со статистикой,
 ,
,
где вектор вероятностей
![]() является МП-оценкой параметра
является МП-оценкой параметра![]() и
и![]() ,
,![]() .
Гипотеза
.
Гипотеза![]() определяет функцию распределения
наблюдения
определяет функцию распределения
наблюдения![]() как полиномиальное распределение:
как полиномиальное распределение:

 .
.
Отсюда функция правдоподобия
![]() и МП-оценка
и МП-оценка![]() доставляет максимальное значение
функции
доставляет максимальное значение
функции![]() (или минимальное значение
(или минимальное значение![]() )
при условиях
)
при условиях![]() и
и![]() .
Для нахождения МП-оценки
.
Для нахождения МП-оценки![]() воспользуемся методом множителей
Лагранжа с функцией,
воспользуемся методом множителей
Лагранжа с функцией,


 .
.
Для определения
![]() требуется решить систему:
требуется решить систему:

![]()

![]()

![]()

![]()

![]()

![]()
 .
.
Таким образом, статистика
![]() имеет вид:
имеет вид:
![]() ,
,
 ,
,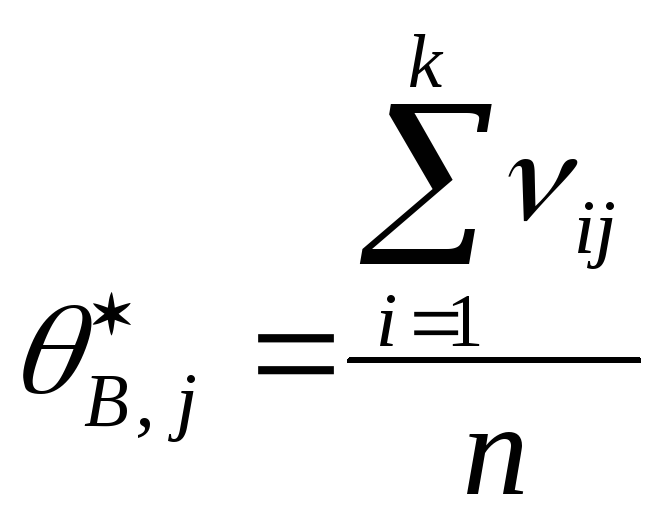 .
.
Согласно теореме Фишера 6.19распределение статистики![]() при
при![]() стремится к распределению
стремится к распределению![]() ,
где
,
где![]() – количество вероятностей
– количество вероятностей![]() и
и![]() – количество параметров (
– количество параметров (![]() параметров
параметров![]() и
и![]() параметров
параметров![]() ).
Легко видеть, что:
).
Легко видеть, что:
![]() ,
,
поэтому распределение статистики
![]() стремится при
стремится при![]() к распределению
к распределению![]() .
.
В качестве критической области
![]() выбирается область вида:
выбирается область вида:
![]()
где
![]() – квантиль уровня
– квантиль уровня![]() распределения
распределения![]() и
и![]() – заданный уровень значимости.
– заданный уровень значимости.
Проверка гипотезы об однородности.
Пусть проводится
![]() независимых серий испытаний: в первой
серии проводится
независимых серий испытаний: в первой
серии проводится![]() независимых испытаний, в каждом из
которых происходит в точности одно из
событий
независимых испытаний, в каждом из
которых происходит в точности одно из
событий![]() ,
…,
,
…,![]() ,
во второй серии проводится
,
во второй серии проводится![]() независимых испытаний, в каждом из
которых происходит в точности одно из
событий
независимых испытаний, в каждом из
которых происходит в точности одно из
событий![]() ,
…,
,
…,![]() ,
и так далее, в
,
и так далее, в![]() -ой
серии проводится
-ой
серии проводится![]() независимых испытаний, в каждом из
которых происходит в точности одно из
событий
независимых испытаний, в каждом из
которых происходит в точности одно из
событий![]() ,
…,
,
…,![]() .
Вероятности событий
.
Вероятности событий![]() неизвестны. По результатам серии
фиксируется количество
неизвестны. По результатам серии
фиксируется количество![]() наступлений каждого события
наступлений каждого события![]() ,
и наблюдение представляет собой вектор
,
и наблюдение представляет собой вектор![]() ,
функция распределения которого является
произведением полиномиальных распределений
,
функция распределения которого является
произведением полиномиальных распределений![]() .
.
Основная гипотеза
![]() заключается в том, что при фиксированном
заключается в том, что при фиксированном![]() и переменном
и переменном![]() события
события![]() имеют одинаковые вероятности, то есть
выполняются равенства,
имеют одинаковые вероятности, то есть
выполняются равенства,
![]() ,
,
…,
![]() ,
,
или, что тоже самое, при фиксированном
![]() и переменном
и переменном![]() вероятности
вероятности![]() при некоторых
при некоторых![]() ,
где вектор вероятностей
,
где вектор вероятностей![]() играет роль параметра:
играет роль параметра:
![]() :
:![]() ,
,
![]() ,
,![]() .
.
Вероятность
![]() ,
поэтому
,
поэтому![]() не входит в вектор параметров
не входит в вектор параметров![]() .
Требуется предложить критерий проверки
гипотезы
.
Требуется предложить критерий проверки
гипотезы![]() .
.
Для решения задачи используется статистика,
 ,
,
где вектор вероятностей
![]() является МП-оценкой параметра
является МП-оценкой параметра![]() и
и![]() .
Гипотеза
.
Гипотеза![]() определяет функцию распределения
наблюдения
определяет функцию распределения
наблюдения![]() как полиномиальное распределение:
как полиномиальное распределение:

 .
.
Таким образом, функция правдоподобия
![]() и МП-оценка
и МП-оценка![]() доставляет максимальное значение
функции
доставляет максимальное значение
функции![]() (или минимальное значение функции
(или минимальное значение функции![]() )
при условии
)
при условии![]() .
Для нахождения МП-оценки
.
Для нахождения МП-оценки![]() используется метод множителей Лагранжа
с функцией,
используется метод множителей Лагранжа
с функцией,

 .
.
Для определения
![]() требуется решить систему:
требуется решить систему:

![]()

![]()

![]()

![]()
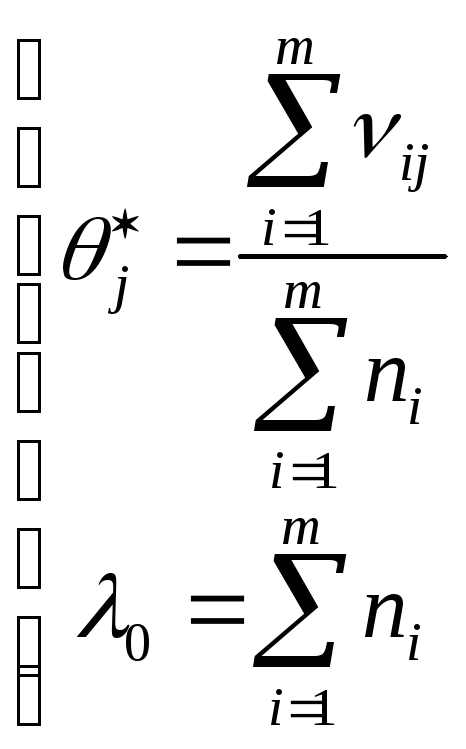 .
.
Таким образом, статистика
![]() имеет вид:
имеет вид:
![]() ,
,
 .
.
Можно показать, что
распределение статистики
![]() при
при![]() стремится к распределению
стремится к распределению![]() ,
где
,
где![]() – количество «независимых»
– количество «независимых»![]() (
(![]() ,
,![]() – при фиксированном
– при фиксированном![]() :
:![]() )
и
)
и![]() – количество параметров
– количество параметров![]() (заметим, что
(заметим, что![]() ).
).
В качестве критической области
![]() выбирается область вида:
выбирается область вида:
![]() ,
,
где
![]() – квантиль уровня
– квантиль уровня![]() распределения
распределения![]() и
и![]() – заданный уровень значимости.
– заданный уровень значимости.
