
Рекомендации по сдаче экзамена
.doc-
Что это за текст такой
Пункт 1 – это попытка неформально описать, на основе каких объектов строится изложение. Он написан только для того, чтобы вы понимали, о чем идет речь и почему в том или ином случае нужно использовать какое-то обозначение, например, почему при определении графа как упорядоченной пары необходимо записывать компоненты этой пары в треугольных скобках.
Пункт 2 – это примеры, иллюстрирующие пункт один. В частности, там указано определение графа, как вы должны его воспроизводить на экзамене.
Пункт 3 описывает, что я жду от вас при ответе на каждый из вопросов. Разумеется, я не раскрою сам ответ на вопрос (для этого мне надо было бы набрать все мои лекции), но я напишу, что именно надо осветить при своем ответе. Естественно, некоторые расширения ответа приветствуются. Если вам покажется, что вы чего-то не знаете (не было в лекциях, или соответствующая их часть почему-то недоступна), можете написать мне – я либо наберу это, если времени хватит, либо расскажу на консультации.
-
Нотация
Пусть имеются некоторый
набор различных объектов
![]() .
Будем составлять последовательности
объектов
.
Будем составлять последовательности
объектов
![]() из
этого набора. Длиной (размером, можностью)
последовательности
из
этого набора. Длиной (размером, можностью)
последовательности
![]() будет называться число
будет называться число
![]() .
В зависимости от того, какие
последовательности будут считаться
одинаковыми и по каким правилам они
могут составляться, будем говорить,
что:
.
В зависимости от того, какие
последовательности будут считаться
одинаковыми и по каким правилам они
могут составляться, будем говорить,
что:
-
 – множество, если
каждый объект последовательности
входит в нее только один раз, и при этом
две последовательности одинаковы, если
различаются только порядком чередования
объектов. Обозначать множество будем
путем взятия его элементов в фигурные
скобки (например, множества
– множество, если
каждый объект последовательности
входит в нее только один раз, и при этом
две последовательности одинаковы, если
различаются только порядком чередования
объектов. Обозначать множество будем
путем взятия его элементов в фигурные
скобки (например, множества
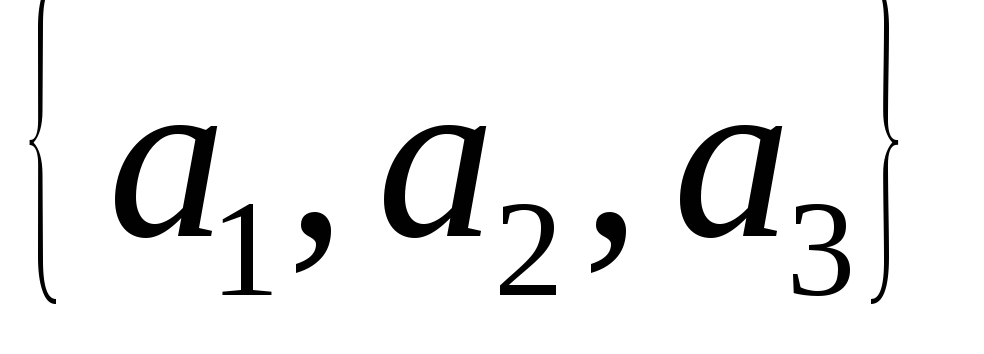 и
и
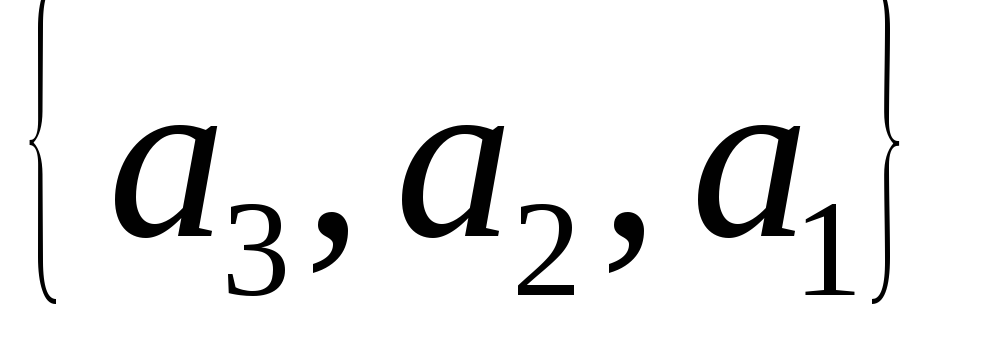 совпадают).
совпадают). -
 – мультимножество
(комплект), если объекты могут входить
в последовательность более одного
раза, и две последовательности одинаковы,
если различаются только порядком
чередования объектов. Обозначать
мультимножество будем путем взятия
его элементов в круглые скобки (например,
мультимножества
– мультимножество
(комплект), если объекты могут входить
в последовательность более одного
раза, и две последовательности одинаковы,
если различаются только порядком
чередования объектов. Обозначать
мультимножество будем путем взятия
его элементов в круглые скобки (например,
мультимножества
 и
и
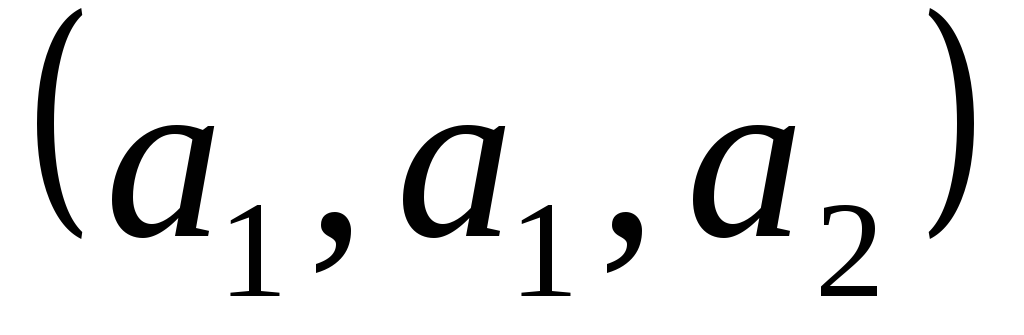 одинаковы).
одинаковы). -
 – вектор (кортеж),
если объекты могут входить в
последовательность более одного раза,
и две последовательности различны,
если они различаются хотя бы в одной
позиции (в частности, если имеют разную
длину). Обозначать вектор будем путем
взятия его элементов в треугольные
скобки (например, векторы
– вектор (кортеж),
если объекты могут входить в
последовательность более одного раза,
и две последовательности различны,
если они различаются хотя бы в одной
позиции (в частности, если имеют разную
длину). Обозначать вектор будем путем
взятия его элементов в треугольные
скобки (например, векторы
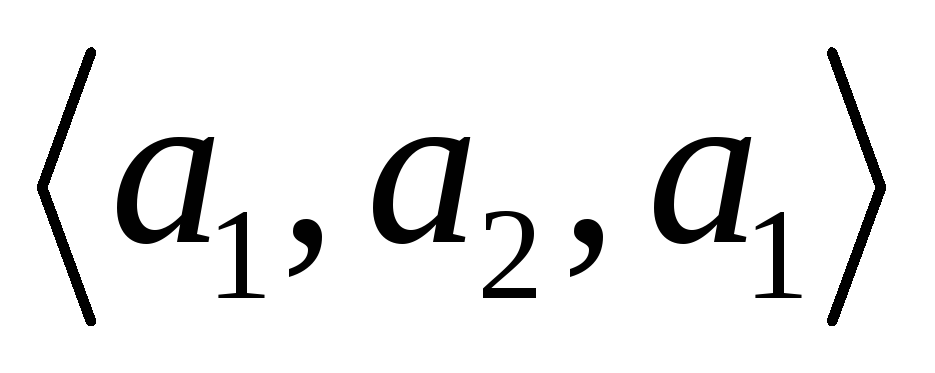 ,
,
 и
и
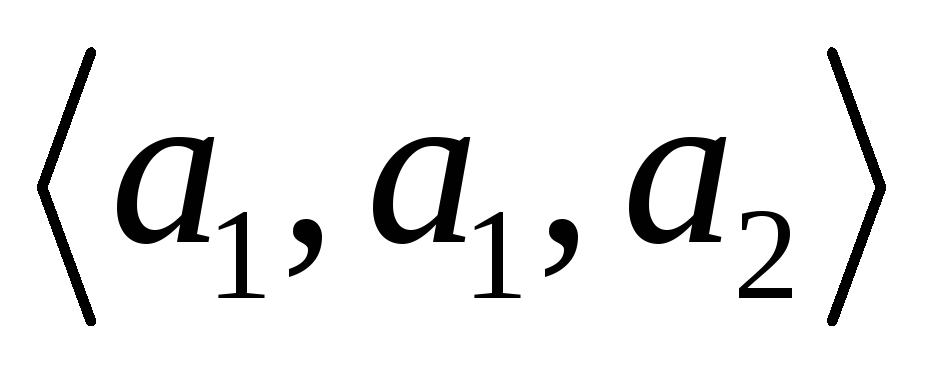 различны).
различны). -
 – упорядоченное
множество, если объекты могут входить
в последовательность только один раз,
и две последовательности различны,
если они различаются хотя бы в одной
позиции (в частности, если имеют разную
длину). Обозначать упорядоченное
множество будем путем взятия его
элементов в квадратные скобки (например,
упорядоченные множества
– упорядоченное
множество, если объекты могут входить
в последовательность только один раз,
и две последовательности различны,
если они различаются хотя бы в одной
позиции (в частности, если имеют разную
длину). Обозначать упорядоченное
множество будем путем взятия его
элементов в квадратные скобки (например,
упорядоченные множества
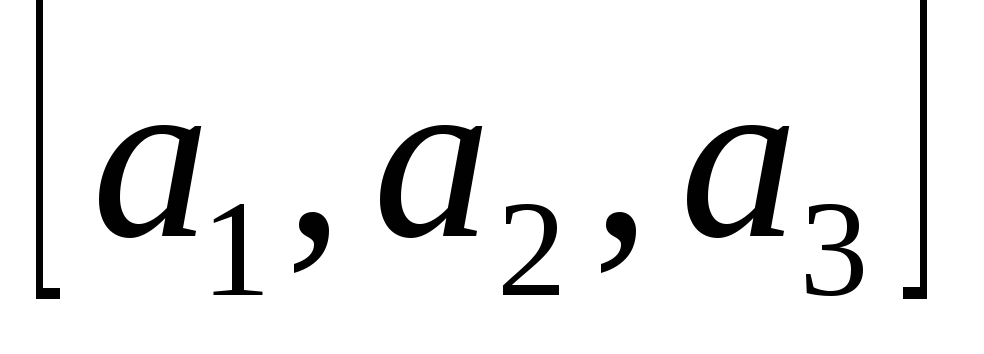 ,
,
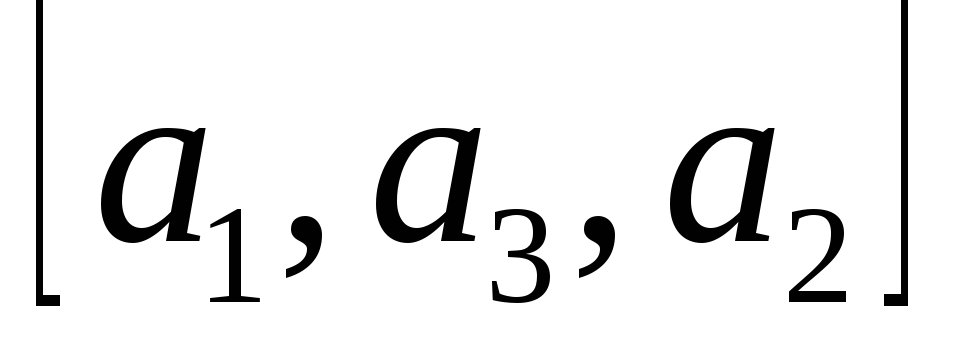 и
и
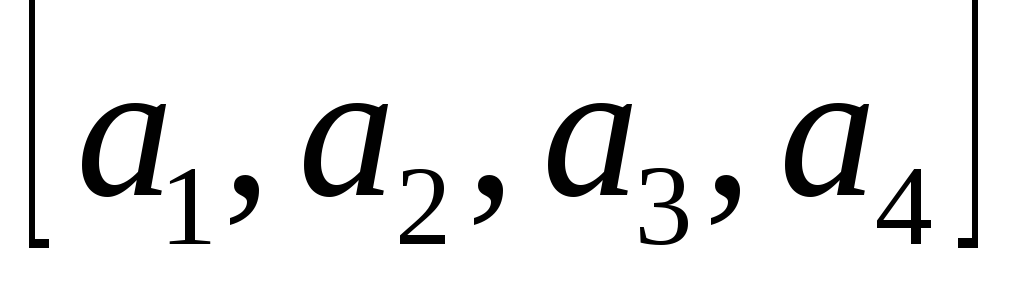 различны).
различны).
-
Некоторые определения
В соответствии с введенными выше обозначениями, можно определить уже знакомые нам объекты:
-
Сочетание – это подмножество (не важен порядок, каждый объект входит в сочетание только один раз).
-
Размещение – это упорядоченное подмножество (важен порядок, каждый объект входит в размещение только один раз).
-
Сочетание с повторениями – это «мультиподмножество» (не важен порядок, каждый объект входит в сочетание с повторениями один или более раз).
-
Размещение с повторениями – это вектор (важен порядок, каждый объект входит в сочетание с повторениями один или более раз).
-
Обыкновенный граф – это упорядоченная пара
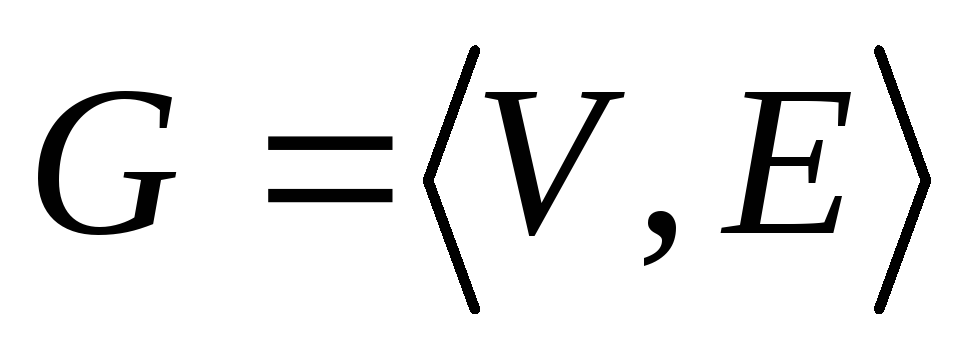 ,
где
,
где
 –
конечное непустое множество вершин,
–
конечное непустое множество вершин,
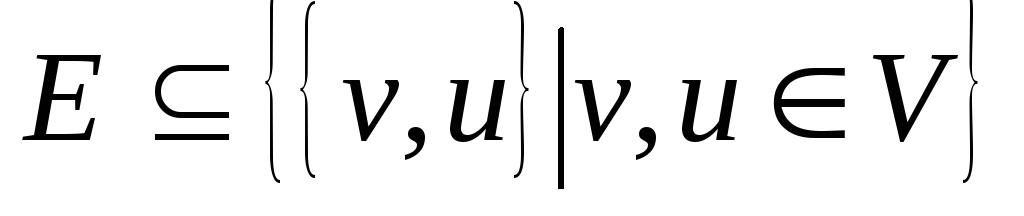 .
То есть:
.
То есть:
 – подмножество
множества двухэлементных подмножеств
– подмножество
множества двухэлементных подмножеств
 .
Замечательно, что при таком определении
входящие в
.
Замечательно, что при таком определении
входящие в
 пары автоматически
образуются различными элементами, т.
к. множество не может содержать двух
одинаковых элементов.
пары автоматически
образуются различными элементами, т.
к. множество не может содержать двух
одинаковых элементов.
-
Содержание вопросов
Здесь я напишу, что хочу видеть в вашем ответе на каждый из вопросов.
-
Правила сложения и умножения. Принцип Дирихле. Числа сочетаний и размещений (с повторениями и без повторений).
-
Бином Ньютона, полиномиальная формула. Тождество Паскаля. Свойства биномиальных и полиномиальных коэффициентов.
-
Формула включений и исключений.
-
Рекуррентные соотношения и формальные ряды. Действия с формальными рядами.
-
Линейные стационарные однородные рекуррентные соотношения и метод их решения. Последовательность Фибоначчи.
-
Комбинаторика разбиений. Рекуррентные соотношения для упорядоченных и неупорядоченных разбиений. Формула Харди-Рамануджана. Диаграммная техника.
-
Преобразование Абеля и суммирование по частям.
-
Простейшие оценки факториалов и биномиальных коэффициентов. Формула Стирлинга. Асимптотика для биномиальных коэффициентов.
В этих билетах все как было в лекциях. Для формулы включений и исключений хочу доказательство, для последовательности Фибоначчи – ее определение и вывод формулы общего члена. Свойства биномиальных и полиномиальных коэффициентов – с доказательствами, как на лекциях. Формула Харди-Рамануджана – просто формула, без доказательства, конечно. Диаграммная техника – описание и пример использования, как было на лекции.
-
Графы и их разновидности. Важнейшие семейства графов.
Основное определение
обыкновенного графа. Разновидности
графов (обыкновенные, ориентированные,
мультиграфы, графы с петлями и другие,
если вы о них знаете) и то, как они
получаются путем уточнения понимания
компоненты
![]() .
Семейств – сколько вспомните, столько
и приведите (с определениями, конечно,
а не просто перечисление). Хватит штук
пять.
.
Семейств – сколько вспомните, столько
и приведите (с определениями, конечно,
а не просто перечисление). Хватит штук
пять.
-
Изоморфизм графов. Вложение и пересечение графов. Симметрия графов.
Определение обыкновенного графа, определение изоморфизма, вложения и пересечения, разные постановки задач. Определение автоморфизма графа.
-
Групповые свойства множества автоморфизмов графа.
Здесь нужно определение автоморфизма, группы, операции композиции двух автоморфизмов и доказательство того, что множество автоморфизмов с этой операцией образует группу. Там надо проверить ассоциативность, наличие единичного элемента и наличие обратного элемента. Вроде просто.
-
Понятие об инварианте. Характеристики инвариантов. Примеры простейших инвариантов.
-
Связность в графах и орграфах. Слабая, односторонняя и сильная связность ориентированных графов.
Тут все по лекциям. Характеристики инвариантов – вычислительная сложность и разрешающая способность. Последняя нуждается в определении.
-
Деревья. Различные определения деревьев и их эквивалентность.
Возьмите три определения дерева (какие вам нравится) и докажите их эквивалентность. Обычно берут такие:
-
Дерево – связный граф, не имеющий циклов;
-
Дерево – связный граф, у которого количество ребер на одно меньше, чем количество вершин;
-
Дерево – граф без циклов, такой, что добавление любого ребра к нему образует цикл.
Доказательства вроде совсем простые. Естественно, нельзя привлекать к доказательству формулу для цикломатического числа графа, так как она и выводится при помощи этих свойств деревьев.
-
Деревья. Коды Прюфера. Формула Кэли.
Определение дерева (любое). Алгоритмы построения кода Прюфера и восстановления дерева по коду (без доказательств). Вывод формулы Кэли при помощи кодов Прюфера. Будьте осторожны: кодируются ПОМЕЧЕННЫЕ деревья, так что и формула верна для ПОМЕЧЕННЫХ же деревьев.
-
Деревья. Изоморфизм деревьев.
Определение дерева (любое). Тут мне нужно определение порядка на множестве деревьев. Рассказывалось на лекции.
-
Структуры данных на основе деревьев. Бинарные деревья поиска и бинарные кучи. Декартово дерево и алгоритм его построения.
-
Лес непересекающихся множеств и подсчет числа компонент связности в обыкновенных графах.
-
Каркас. Построение каркаса минимального веса: алгоритмы Крускала и Прима.
Для алгоритма Крускала доказательство корректности нужно, для Прима – не нужно.
-
Задача о кратчайших путях. Алгоритм Флойда.
-
Задача о кратчайших путях. Алгоритм Дейкстры.
Здесь только постановки, формулировки и условия применимости.
-
Обходы графов. Обход в глубину. Дерево обхода в глубину и его применения: поиск точек сочленения, топологическая сортировка.
-
Обходы графов. Обход в ширину. Дерево обхода в ширину и его свойства.
-
Подграфы и их виды. Остовные подграфы. Каркас, клика, независимое подмножество вершин.
-
Пространство подграфов. Подграфы четной степени и их свойства.
-
Пространство подграфов. Фундаментальное множество циклов и метод его построения.
Без комментариев.
-
Задача о клике. Переборный алгоритм и простейшие методы сокращения перебора. Алгоритм Брона-Кербоша.
Постановка задачи, описание переборного алгоритма и какие-нибудь способы сократить перебор. Про Брона-Кербоша – вкратце идеи этого метода.
-
Задача коммивояжера. Динамический алгоритм. Алгоритм ближайшего соседа.
-
Хроматическая функция графа.
Определение, способ вычисления. Факт: является инвариантом (почему?)
-
Вершинные и реберные раскраски графов. Алгоритм вершинной раскраски. Теорема Визинга.
Без комментариев.
-
Теорема Эйлера для планарных графов. Теоремы о 6- и 5-раскраске планарных графов.
Здесь все с доказательствами. Поскольку доказательство теоремы Эйлера весьма непростое и требует знания математики, которую вам еще в общем-то не читали, для нее ограничьтесь схемой доказательства.
-
Паросочетания и реберные покрытия. Метод увеличивающих путей.
Постановка задач о паросочетаниях и реберных покрытиях, сводимость второй к первой. Определение увеличивающегося пути и его свойства.
-
Матроиды. Матричный матроид и графовый матроид
-
Матроиды. Жадный алгоритм и теорема Рао-Эдмондса.
Что такое матроид. Про матричный и графовый матроиды мне нужно определение и доказательство того, что это матроиды. Про жадный алгоритм – описание, про теоремы – формулировка и доказательство.
