
- •1. Основы метрологии 10
- •2. Основы стандартизации. Взаимозаменяемость 95
- •3. Основы сертификации 209
- •2. Основы стандартизации. Взаимозаменяемость 84
- •Введение
- •Основы метрологии
- •Термины и определения
- •Этапы становления метрологии
- •Международная система единиц физических величин
- •Единицы измерений физических единиц
- •Кратные и дольные единицы
- •Кратные и дольные единицы
- •Размерность измеряемой величины
- •Размерность основных физических величин системы си
- •Обобщенные свойства шкал измерений физических величин
- •Виды и методы измерений
- •Классификация средств измерений
- •Методы измерений физических величин
- •Погрешности измерений
- •Типы погрешностей
- •Погрешности подразделяют по происхождению
- •Погрешности классифицируются по закономерностям проявления
- •Нормальный закон распределения случайных погрешностей (закон Гаусса)
- •Равномерный закон распределения случайных погрешностей
- •Закон сложения случайных погрешностей
- •Приемы вычислений, позволяющие избежать операций с большими числами
- •Примеры переведения систематической погрешности в случайную (рандомизация)
- •Согласование точности обработки и точности самих измерений
- •Погрешности средств измерений
- •Номинальные значения влияющих величин при нормальных условиях
- •Классы точности средств измерений и нормирование погрешностей
- •Обозначения классов точности средств измерений
- •Математическая обработка результатов однократных измерений Однократные измерения с точным оцениванием погрешности
- •Зависимость погрешности результата прямых однократных измерений (р) от соотношения / s .
- •Значения в зависимости от соотношения / s .
- •Прямые однократные измерения с приближенным оцениванием погрешности
- •Погрешности косвенных измерений
- •Абсолютные погрешности косвенных измерений
- •Математическая обработка результатов прямых многократных равноточных измерений
- •1. Определяются точечные оценки закона распределения результатов измерений.
- •2. Определяют закон распределения результатов измерений либо случайных погрешностей измерений.
- •3. Оценка закона распределения по статистическим критериям
- •4. Определение доверительных границ случайной погрешности
- •Значения коэффициента Стьюдента при доверительной вероятности
- •Четырехкратное измерение сопротивления катушки
- •5. Определяют границы неисключенной систематической погрешности результата измерений.
- •6. Определяют доверительный интервал погрешности результата измерения ( ).
- •Критерии исключения грубых погрешностей
- •Значения критерия Романовского
- •Округление результатов измерений
- •Единство измерений. Поверочные схемы. Понятие о поверке и калибровке Единство измерений
- •Поверка и калибровка средств измерений
- •Государственный метрологический контроль и надзор
- •Основы стандартизации. Взаимозаменяемость
- •Техническое регулирование, цели и средства
- •Виды взаимозаменяемости
- •Классификация отклонений геометрических параметров
- •Отклонения и допуски размеров
- •Основные ряды линейных размеров
- •Соединения и посадки
- •Системы образования посадок
- •Выбор системы образования посадок.
- •Признаки построения есдп
- •Области применения квалитетов
- •Посадки подшипников качения
- •Область применения классов точности
- •Допуски формы валов и корпусов
- •Шероховатость поверхностей
- •Допуски торцевого биения заплечиков вала
- •Допуски торцевого биения заплечиков корпуса
- •Общие рекомендации по выбору посадок
- •Посадки с натягом
- •Посадки с зазором
- •Переходные посадки
- •Предельные отклонения размеров с неуказанными допусками
- •Допуски свободных размеров
- •Отклонения и допуски формы
- •Отклонения формы поверхностей
- •Отклонения и допуски расположения
- •Виды отклонений расположения
- •Суммарные допуски формы и расположения
- •Зависимые допуски расположения и формы
- •Размерные цепи
- •Виды звеньев размерной цепи
- •Методы достижения точности замыкающего звена
- •Решение обратной задачи (задачи технолога) методом полной взаимозаменяемости (пример)
- •Решение обратной задачи (технолога) вероятностным методом
- •Решения прямой задачи (задачи конструктора)
- •Шероховатость поверхности
- •Волнистость поверхности
- •Шпоночные соединения
- •Допуски и посадки шлицевых соединений.
- •Виды центрирования шлицевых соединений
- •. Резьбовые соединения
- •Зубчатые передачи, допуски
- •Калибры гладкие
- •Область технического регулирования. Цели и принципы стандартизации. Виды стандартов
- •Цели стандартизации в рф
- •Принципы стандартизации
- •Стандарты организаций.
- •Виды стандартов, действующих на территории рф
- •.Этапы развития стандартизации
- •Система органов и служб стандартизации в Российской Федерации
- •Функции национального органа по стандартизации
- •Правила разработки и утверждения технических регламентов и национальных стандартов
- •Стандарты организаций.
- •Основы теории стандартизации Элементы теории стандартизации
- •Естественнонаучная база стандартизации
- •Виды стандартов
- •Информационное обеспечение стандартизации
- •Основы сертификации
- •Цели и принципы сертификации
- •Термины и определения сертификации
- •Виды сертификации
- •Средства и методы сертификации. Испытательная (измерительная) лаборатория
- •Измерительная (испытательная) лаборатория
- •Обязательное подтверждение соответствия. Схемы сертификации
- •Схемы обязательной сертификации №№ 1-10
- •Схемы обязательной сертификации
- •Системы сертификации
- •Схемы сертификации услуг (работ).
- •Перечень схем сертификации услуг
- •Порядок проведения сертификации
- •Функции органа по сертификации:
- •Принципы аккредитации:
- •Полномочия органов по аккредитации
- •Сертификация импортной продукции
- •Подтверждение сертификации отечественных товаров
- •Государственный контроль (надзор) за соблюдением требований технических регламентов и государственных стандартов
- •Юридическая ответственность за несоблюдение технических регламентов, стандартов, правил сертификации и метрологии
- •Сертификация систем менеджмента качества (смк)
- •Система экологического менеджмента (сэм)
- •3.13 Управление качеством на судостроительном предприятии
- •Литература
Обобщенные свойства шкал измерений физических величин
Свойства |
Шкала порядка |
Шкала интервалов |
Шкала отношений |
Реализуемый способ сравнения |
Qi>Qj, Qi<Qj ,
|
|
|
|
|||
Результат измерения |
ранжированный ряд |
разность |
числовое значение (размер) |
Начало отсчета |
нет |
условный ноль |
естественное начало отсчета |
Математические операции |
не разрешены; разрешены логические операции |
определены аддитивные операции; мультипликативные – не разрешены |
все математические операции разрешены |
Примеры |
шкалы интенсивности землетрясения, твердости минералов, чувствительности фотопленок |
шкала времени, температурные шкалы Цельсия, Фаренгейта |
относительные шкалы скорости, напряжения, температурная Кельвина и др. |
Виды и методы измерений
Термином «измерение» чаще называют процедуру инструментального определения значений абсолютных или удельных (относительных) численных характеристик отдельных свойств.
Измерение физической величины – познавательный процесс, при котором путем физического эксперимента данная физическая величина (ФВ) сравнивается с известной ФВ, принятой за единицу.
Процесс измерения состоит, с одной стороны, из восприятия и отображения физической величины, а с другой стороны, из нормирования, т.е. присвоения измеряемой величине определенной числового значения. При этом должны быть соблюдены два условия:
подлежащая измерению физическая величина однозначно определяема;
единица измерения установлена соглашением.
Физические величины (ФВ) подразделяют на измеряемые и оцениваемые. Измеряемые физические величины могут быть выражены количественно в виде определенного числа установленных единиц измерения. С этими величинами могут быть произведены математические операции сложения (вычитания), умножения (деления) в зависимости от типа шкалы (см. выше). Результат измерения – числовое значение физической величины, полученное путем её измерения. Результат представляется именованным или неименованным числом.
Физические величины, для которых по тем или иным причинам не может быть введена единица измерения, могут быть только оценены. Оценивание – операция приписывания данной физической величине определенного числа, проводимая по установленным правилам. Оценивание величин осуществляется при помощи шкалы порядка.
Для измеряемой ФВ значение её размера Q получают в результате измерения и вычисления в соответствии с основным уравнением измерения (по шкале отношений): Q =q[Q], где q – числовое значение ФВ (в принятых единицах),
[Q] – единица ФВ (измерение производится в этих единицах).
Получение информации о размере физических (или нефизических) величин, характеризующих свойства объекта, является содержанием любого измерения.
Цель любого измерения – в получении информации об истинном значении измеряемой величины. Однако при измерении полностью объективное и абсолютное истинное значение измеряемой величины получить нельзя, так как размер измеряемого всегда содержит элемент неопределенности и поэтому остается неизвестным. Поэтому задача измерения состоит не в определении абсолютно истинного значения измеряемой величины, а в том, чтобы узнать о нем, получить о нем достоверную информацию, оценить ее и выразить в той или иной приемлемой форме.
Обычно экспериментальным путем в результате точных измерений получают значение определяемой величины, близкое к истинному, и называют его действительным значением измеренной величины. Действительное значение измеряемой величины получено экспериментальным путем с помощью высокоточных средств измерений, оно близко к истинному и при расчетах погрешностей может использоваться вместо него.
Все виды измерений разделяются по приемам получения результата на группы: прямые, косвенные, совокупные и совместные.
Прямыми называются измерения, результат которых получается непосредственно из опытных данных. Например, измерения температуры воздуха термометром, силы электрического тока амперметром, промежутка времени секундомером – это прямые измерения. Прямые измерения лежат в основе других, более сложных, видов измерений.
Косвенными называются измерения, при которых искомая величина непосредственно не может быть измерена, а её значение находят на основании известной зависимости между этой величиной и величинами, полученными в результате прямых измерений. Простейшим примером косвенного измерения служит определение объема тела по результатам прямых измерений его линейных размеров. Результатом косвенного измерения является, например, сопротивление резистора R, которое находится из уравнения R= U/I , в которое подставляют полученные прямыми измерениями значения падения напряжения на резисторе U и силы тока I через него.
Совокупные измерения – это проводимые одновременно измерения нескольких одноименных величин, при которых их искомые значения находят решением системы уравнений, составленных по результатам прямых измерений различных сочетаний этих величин. При этом искомое значение физической величины получают путем сравнения (сопоставления) измеряемых величин с известной величиной. Совокупные измерения используются, например, при определении неизвестной емкости по известной емкости одного из конденсаторов и по результатам измерений различных сочетаний емкостей.
Совместные измерения – одновременные измерения двух или нескольких неодноименных величин для установления зависимости между ними. Например, на основании двух одновременных измерений (температуры и размера) определяют коэффициент линейного расширения твердого тела. Другим примером совместных измерений может служить нахождение коэффициентов, определяющих температурную зависимость сопротивления (ТКС) проводников.
По характеру зависимости измеряемой величины от времени методы измерения подразделяются на статические (измеряемая величина принимается за неизменную в течение времени измерения) и динамические (измеряемая величина является непостоянной в течении времени измерения, по ходу измерения требуется фиксация моментов времени).
По способу выражения результатов измерений измерения делят на абсолютные и относительные измерения.
Абсолютные измерения основаны на прямых измерениях величины. Абсолютное, или фундаментальное, измерение – это прямое измерение одного или нескольких физических размеров свойств с использованием основных натуральных единиц измерений и (или) значений физических констант. Например, определение веса тела путем умножения значения массы на физическую константу g (ускорение свободного падения) является абсолютным измерением.
Относительные измерения базируются на сравнении величины с одноименной, принятой за единицу. При этом искомое значение зависит от используемой единицы измерений.
Статистические измерения используются для набора статистики, они связаны с определением характеристик случайных процессов.
Равноточные измерения – измерения с одинаковой точностью определения измеряемой величины, выполняемые одинаковыми по точности средствами измерений в одних и тех же условиях.
Неравноточные измерения – это ряд измерений какого-либо размера, выполненных различными по точности средствами измерений и (или) в разных условиях.
Однократное измерение – измерение, выполненное один раз. Измерения, выполненные 2 или 3 раза, также относятся к однократным.
Многократное измерение – измерение одного и того же размера, результат которого получают из нескольких последовательных измерений (не менее 4-х), т.е. это измерение, состоящее из ряда однократных измерений. При числе измерений (наблюдений) не менее четырех результат может быть обработан методами математической статистики.
Физико-технические и технические измерения – измерения при использовании единиц физических величин. К таким измерениям относятся: механические, электрические, оптические, тепловые и тр.
Метрологические измерения – измерения с помощью рабочих эталонов единиц физических величин для передачи их размера рабочим средствам измерений, а также поверочные измерения для определения погрешностей средств измерений. Эти измерения осуществляются для измерительных же целей, т.е. являются метрологическими.
Абсолютное, или фундаментальное, измерение – это прямое измерение одного или нескольких физических размеров свойств с использованием основных натуральных единиц измерений и (или) значений физических констант.
Относительное измерение – измерение отношения измеряемой величины к одноименной величине, играющей роль единицы измерения, или измерения величины по отношению к одноименной величине, принимаемой за исходную (эталонную, базовую).



 ,
,

 - изменяемая
величина;
- изменяемая
величина;
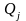 - величина с которой производят
сравнение; [Q]
– единица измерения, q
– числовое значение
- величина с которой производят
сравнение; [Q]
– единица измерения, q
– числовое значение