Четырехкратное измерение сопротивления катушки

Результат наблюдения xi , Ом	Отклонение результата наблюдения, Δί , Ом	Квадрат отклонения, Δί2, Ом2
100,0078	-0,0008
100,0084	-0,0002
100,0087	+0,0001
100,0095	+0,0009

4. Найдем оценку СКО результатов наблюдений :

Ом.

5. Найдем оценку СКО результата измерения (СКО среднеарифметического):

Ом.

6. По Таблице 3.2 для n=4 и Р=0,99 найдем коэффициент Стъюдента t_Р =5,84.

7. Определим доверительные границы погрешности результата измерения путем умножения t_Р на :

Ом.

Результат измерения запишем в следующем виде:

Ом при Р_д=0,99.

5. Определяют границы неисключенной систематической погрешности результата измерений.

Эти границы находят нестатистическими методами. Это границы интервала, внутри которого находится неисключенная систематическая погрешность. Такая погрешность образуется из нескольких составляющих: погрешностей метода измерений, средств измерений, субъективной погрешности оператора. Если погрешности метода измерений и погрешности оператора малы, то границы неисключенной систематической погрешности принимаются равными пределам основных и дополнительных погрешностей средств измерения СИ ( в случае, если случайные составляющие пренебрежимо малы). При определении границ доверительную вероятность принимают раной доверительной вероятности , принятой при определении границ случайной погрешности.

6. Определяют доверительный интервал погрешности результата измерения ( ).

определяют суммированием СКО случайной составляющей погрешности и границ неисключенной систематической составляющей погрешности в зависимости от соотношения / .

7. Записывают результаты измерения.

Результаты измерения записывают в виде при доверительной вероятности .

Если данные о законах распределения составляющих погрешности отсутствуют, результаты приводят в следующем виде: , n, при .

9. Критерии исключения грубых погрешностей

Критерий «трех сигм»

Для результатов измерений (наблюдений), распределенных по нормальному закону (закону Гаусса) считается, что результат, возникающий с вероятностью Р<0,003 ( так называемый уровень значимости q 0,3%) маловероятен, и его следует считать промахом. Таким образом, если , считается промахом. – оценка среднеквадратичного отклонения (СКО) результата наблюдения; – среднеарифметическое значение. Величины и вычисляются без учета экстремальных значений . Данный критерий используется предпочтительно при числе наблюдений n 20…50.

Пример 1(а). Сопротивление катушки измеряют 31 раз. =100,0086 Ом. СКО результата наблюдения Ом. Найти СКО результата измерения и определить доверительные границы случайной погрешности результата измерений при Р = 0,95.

Решение. СКО результата измерения (СКО среднеарифметического) составит:

(Ом).

Доверительные границы погрешности результата измерения (СКО среднеарифметического) составляют при Р = 0,95:

(Ом) (Ом).

Таким образом, 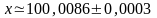Ом (Р = 0,95).

_{Пример 1(б)}. Сопротивление катушки измеряют 31 раз. По результатам 30 наблюдений _{= 100,0086 Ом. СКО результата наблюдения (рассчитано из 30 наблюдений) 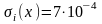Ом. Является ли 31-ый результат Ом промахом?}

_{Решение. По критерию «трех сигм» промахом будет считаться результат, для которого 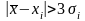, т.е.} Ом и Ом. Результат 31-го наблюдения 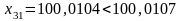_{Ом, т.е. результат данного наблюдения меньше максимально допустимого, но больше минимально допустимого, промахом не является и его следует включить в статистическую обработку.}

Критерий Романовского.

Если число измерений менее 20 (n<20), одним из рекомендованных критериев исключения грубых погрешностей является критерий Романовского. Для проверяемого значения вычисляют отношение

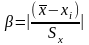
и сравнивают с табличным значением критерия Романовского . Значения критерия , в зависимости от числа наблюдений n и уровня значимости q (так называемой вероятности невыполнения), вычисляют по таблицам.

Таблица 13