§ 15. Решение волнового уравнения в случае свободной материальной точки

Для свободной материальной точки .

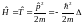, тогда переходим к стационарному уравнению Шредингера.

Это трехмерная задача

Оператор Лапласа

Оператор представим в виде суммы трех независимых операторов, которые коммутируют. В этом случае можно разделить переменные.

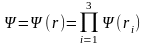
Тогда стационарное уравнение Шредингера запишется в виде

,

где

Для имеем

.

Обозначим

.

Тогда

Решение этого уравнения

Так как частица свободная, то импульс этой частицы сохраняется. Значит, сохраняется направление движения частицы.

Мы выбираем движение частицы по направлению оси x. Тогда в силу сохранения импульса имеем .

Для трехмерного случая

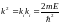
Полная волновая функция

(15.1)

Рассмотрим теперь коммутатор

Так как импульс коммутирует с и не зависит явно от времени, тогда . Из этого следует:

-интеграл движения.

Собственная функция оператора импульса является решением волнового уравнения.

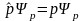
Найдем собственные значения оператора импульса.

{используем, что , т. е. } =

= .

Тогда собственное значение оператора :

Это первое дебройлевское соотношение.

Из (15.1) вводится - второе дебройлевское соотношение.

Используем, что

Уравнение (15.1) удовлетворяет собственной функции оператора импульса.

§ 16. Собственный механический момент (спин). Спиновая переменная волновой функции. Нормировка функций.

Рассмотрим Na. У него есть желтая линия . Возникает при переходе с уровня 3p на 3s.

Первоначально ее длина была 5892

Было обнаружено, что эта линия расщепляется на две: дублет.

Возникла идея расщепления уровня 3p на два, тогда можно объяснить возникновение двух линий.

Их длины: 5896 и 5890 .

В 1925 г. Была предложена гипотеза спина, т. е. собственного механического момента.

У электрона спиновое число s= .

Впоследствии Паули ввел спин в теорию.

Если имеем одну частицу, то она характеризуется орбитальным квантовым числом .

Составная частица (атом) состоит из многих микрочастиц. Можно рассматривать эту составную частицу вцелом и приписать ей момент , который описывает орбитальное движение частицы как целого.

Энергетический уровень этой составной частицы в некоторых полях будет зависеть от орбитальных моментов микрочастиц .

Эти моменты являются внутренним свойством этой составной частицы.

Можно рассматривать 2 момента:

1. . Этот момент описывает внутреннее движение частицы (относительно центра инерции)

2. Частица сама движется по некоторой траектории.

У частицы есть еще квантовое число 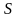, характеризующее собственный механический момент.

Вводят оператор собственного механического момента:

По аналогии

Спин – внутреннее свойство частицы. Его смысл – у частицы есть внутренний параметр, который реагирует на вращение координат независимо от места положения частицы.

Рассмотрим одну частицу – система с 3 степенями свободы. Задача решается в - представлении.

,

но есть еще внутренний параметр – спин, тогда .

Здесь 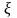- переменная (пространственная координата) и (спиновая переменная, а именнопроекция спина на ось ).

Здесь мы рассматриваем стационарную задачу, поэтому далее , .

Скалярное произведение теперь запишем в виде

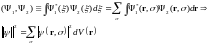
Вероятность обнаружения частицы в объеме вблизи точки :

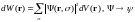
Если хотим найти реализацию конкретного значения :

Рассмотрим действие операторов в пространстве четырех переменных

Было известно

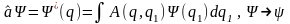(16.1)

Обобщим (16.1) на случай четырех переменных:

(16.2)

Рассмотрим случай когда действует только на спиновую переменную. В этом случае ядро будет следующим

и интеграл (16.2) переходит в интеграл:

Тогда

Переменная здесь не играет большой роли. В дальнейшем будем ее опускать, тогда

Функция имеет 2s+1 переменную.

Ядро в дискретных переменных вырождается в матрицу, т. е. это есть матрица размером .