Градиентный метод с дроблением шага.

В методе наискорейшего спуска на каждом шаге необходимо решать задачу одномерной минимизации, для чего используется один из методов одномерной минимизации, предполагающих наличие одного минимума внутри некоторого отрезка, в чем не всегда бывает уверенность. Поэтому широко используется градиентный метод без одномерной минимизации, основанный на пошаговой корректировке коэффициента . По-прежнему расчетной будет формула

,

задаемся некоторым . Полагаем . Если при этом , то удваиваем шаг: . Процесс удвоения продолжаем до тех пор, пока убывание не прекратится.

Если , то полагаем: , если при этом не произошло уменьшение значения функции, то процесс дробления продолжаем до тех пор, пока не наступит убывание.

Эта логика работает на каждом шаге.

Этот метод сойдется, если выпукла и не является «овражной».

Рисунок 4.3 .6 - блок - схема градиентного метода с дроблением (другой вариант градиентного метода с дроблением шага).

Рисунок 4.3.6Блок-схема градиентного метода с дроблением шага.

Методы нулевого порядка.

В практических задачах нередки случаи, когда минимизируемая функция либо не обладает нужной гладкостью, либо является гладкой, но вычисление производных с нужной точностью является слишком трудоемким. В таких случаях применяют методы минимизации, которые требуют лишь вычисления значений функций, то есть методы 0-го порядка. Из методов этого типа рассмотрим 2 наиболее распространенных: метод покоординатного спуска и метод случайного поиска.

Метод покоординатного спуска.

Суть метода состоит в том, что задав начальное приближение выбирается направление движения по одной из покоординатных осей, причем, на последующих шагах идет циклический перебор направлений по координатным осям.

Наиболее распространенным является метод покоординатного спуска с дроблением шага.

Обозначим - единичный координатный(базисный) вектор, у которого i - я координата равна 1, а остальные равны 0.

Положим ; , -целая часть числа .

Будем иметь

Опишем подробно одну итерацию.

Пусть получено . Будем искать .

Вычислим значение функции в точке и проверим неравенство .

Если это неравенство выполняется, то полагаем

.

В случае, если неравенство не выполняется, то вычисляем и проверим неравенство .

В случае выполнения последнего неравенства полагаем

.

В случае невыполнения обоих неравенств полагаем

,

- параметр метода; .

Последние условия означают, что если за один цикл из n итераций при переборе направлений всех координатных осей с шагом реализовалась хотя бы одна удачная итерация, то длина шага не дробится и сохраняется по крайне мере на протяжении следующего цикла из n итераций.

Если же среди последних n итераций не оказалось ни одной удачной, то шаг дробится.

Сходимость метода обеспечена для гладких функций, несмотря на то, что это метод 0-го порядка. Оказывается, что если не является гладкой, то метод покоординатного спуска может не сходится к решению.

Другой вариант метода покоординатного спуска может состоять в получении как решения задачи одномерной минимизации:

.

Этот вариант имеет смысл применять в том случае, когда можно найти явно.

Хотя скорость сходимости метода покоординатного спуска невысокая, благодаря его простоте и скромным требованиям к гладкости этот метод довольно широко применяется на практике.

На рисунке 4.1 приведена блок-схема метода покоординатного спуска для функции дух переменных с оптимизацией длины шага.

Пример.

Найти минимум

Напомним, что эту задачу мы решали рассмотренными выше методами и встретились с трудностями в силу ее овражности.

Положим, как и раньше, ;

Находим как решение задачи одномерной минимизации, а именно, ищем , обеспечивающее минимум , это будет .

Отсюда

Далее

;

В результате выполнения 2-й итерации получили точное решение.

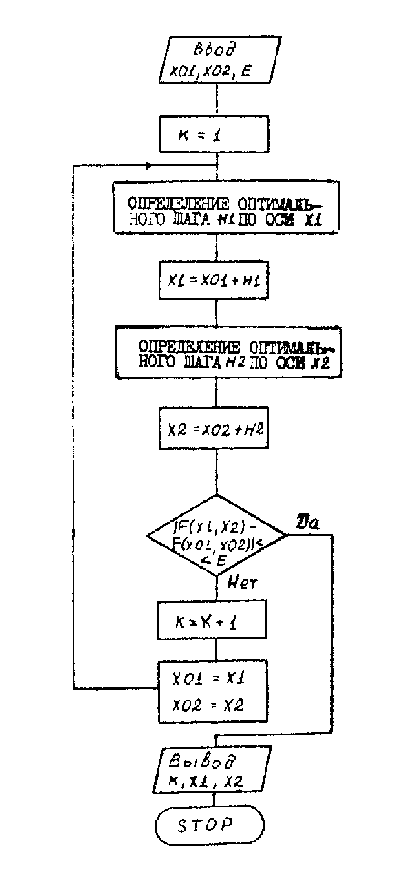
Рисунок 4.4.7 Блок-схема метода покоординатного спуска.