Метод наискорейшего спуска.

Если на каждом шаге выбирать как значение, обеспечивающее , то мы и получим метод наискорейшего спуска, то есть на каждой итерации необходимо решать задачу одномерной минимизации, которая в основном решается численно.

Итак, для того чтобы использовать метод наискорейшего спуска, необходимо задать правила вычислений , (предварительно продифференцировав ), выбрать метод одномерной минимизации.

На рисунке 3.1 представлена укрупненная блок-схема такого алгоритма, где критерием окончания счета выбрана близость градиента нулю. Рассмотрим предыдущий пример. Найти минимум

Методом наискорейшего спуска вычисления будут производится по расчетной формуле

Как и в предыдущих случаях в качестве начального приближения возьмем

на каждой итерации находится классическим методом, то есть приравниванием производной нулю.

Рисунок 4.3.2Блок-схема метода наискорейшего спуска.

Результаты вычислений по итерациям представлены в таблице.

Номер итерации
0	0,06097	0	0
1	0,2778	1,09756	-0,36585
2	-0,06	0,60976	-1,82928
3	0,322	1,0312	-1,96977
4	0,0592	0,8504	-2,6332
5	0,3218	1,0098	-2,6766
6	0,05578	0,95303	-2,8847
7	0,3782	1,00293	-2,8976
8	0,04596	0,98646	-2,975
9		0,99766	-2,9773

Как показано выше, точным решением этой задачи является , проведенные 9 итераций не обеспечили получение приближенного решения с точностью .

Интересным является тот факт, что рассмотренный выше квазиньютоновский метод(тоже метод 1-го порядка) обеспечивает для той же задачи получение точного решения за 2 шага, в то время, как метод наискорейшего спуска требует существенно большего числа итераций.

На рисунке 3.2 для трех рассмотренных выше методов представлены траектории движения из начальной точки в точку минимума .

Сплошная линия соответствует методу наискорейшего спуска, пунктирная - квазиньютоновскому методу, пунктирная с точками - методу Ньютона.

Рисунок 4.3.3Траектория движения из точки в точку минимума функции

Ломаная траектории метода наискорейшего спуска удивляет своим характером.

Изменим немного вид исходной функции. Пусть

.

Нетрудно показать, что точкой минимума и этой функции будет . Применим метод наискорейшего спуска, начав с точки .

Расчетная формула метода имеет вид

,

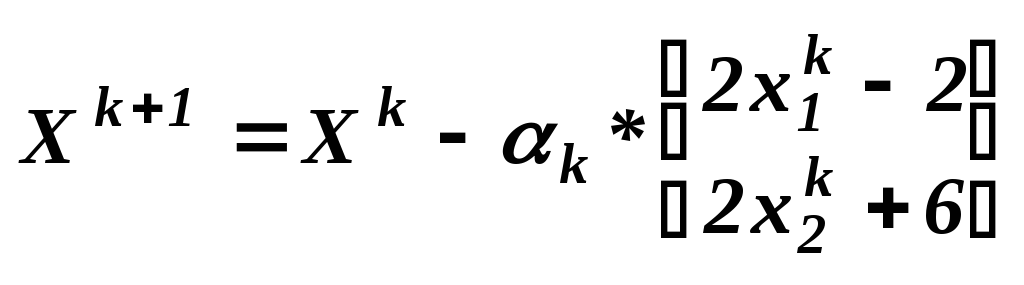Найдем из условия

Отсюда , то есть за один шаг попали в точку минимума.

Чем же разнятся эти задачи, дающие разные по трудоемкости вычислительные процедуры?

Представим линии уровня каждой из функций.

Для

линиями уровня будут кривые

или

Получили каноническое уравнение эллипса, из которого видно, что одна из полуосей в 3 раза меньше другой, то есть эллипс вытянут вдоль оси .

Для линиями уровня будут концентрические окружности с центром в точке .

На рисунке с нанесенными на плоскость линиями уровня представлена траектории движения из точки в точку , соответствующая методу наискорейшего спуска для функции

На рисунке 3.4 то же проделано для функции

Рисунок 4.3.4Траектория движения из точки в точку функции

Рисунок 4.3.5Траектория движения из точки в точку функции

Чем больше вытянуты линии уровня, тем сильнее будет эффект «зигзага» траектории. В этом случае функция имеет так называемый «овражный» характер, то есть небольшое изменение переменной приводит к резкому изменению значений функции, а по переменной функция меняется незначительно. В процессе реализации градиентного метода очередные приближения будут прыгать со склона на склон, что может сильно замедлить сходимость метода. Этой проблеме уделяется достаточно серьезное внимание, в настоящее время существуют специальные методы.