35

Методы многомерной безусловной минимизации. Постановка задачи и классификация методов.

Под задачей многомерной безусловной оптимизации будем понимать задачу нахождения минимума,-вектор n - мерного евклидова пространства; - компоненты вектора . Обычно эта задача записывается как

.

Ниже представлены численные методы, предназначенные для решения этой задачи.

Определение.

Метод, использующий для своей реализации значения , а также ее производных до m-го порядка включительно, называется методом m-го порядка.

Будем рассматривать наиболее применяющиеся методы:

0 - го порядка, использующие только значения ;

1 - го порядка, использующие значения , а также значения ее первых производных;

2 - го порядка, использующие значения , а также значения ее первых и вторых производных.

Все рассматриваемые методы характеризуются тем, что строится некоторая последовательность векторов , имеющая для всех методов, кроме метода случайного поиска, вид

,

k - номер члена последовательности или номер итерации.

Вектор определяет направление -го шага минимизации, - длину этого шага.

Последовательность сходится к точке минимума , если

,

а метод, реализующий такую последовательность, называется сходящимся.

Естественно, что не всегда метод будет сходящимся, поэтому вопросу сходимости при рассмотрении конкретных методов уделяется одно из центральных мест.

Установление факта сходимости и оценка скорости сходимости дает существенную информацию о выбранном методе минимизации.

Поскольку речь идет о численных методах решения, необходимо задавать точность, с которой ищется решение. Приближение имеет точность , если

,

означает норму вектора B. В основном будем использовать норму , где - - я компонента вектора B. В случае использованию других норм будут сделаны специальные оговорки.

Итак, если применяется сходящийся численный алгоритм, необходимо выработать критерии остановки вычислительного процесса, гарантирующие выполнение требования по точности.

Обычно на практике применяются следующие критерии остановки:

1)

2)

3. 

где - малые константы;

- градиент функции , вычисленный в точке .

Напомним, что градиентом функции в точке называется вектор, компоненты которого есть частные производные по компонентам вектора , вычисленные в точке .

Обычно используется либо один критерий, либо два из предложенных, либо все три критерия.

Методы второго порядка.

Напомним, что методом второго порядка называется метод, использующий значения минимизируемой функции, а также значения ее первых и вторых производных. Отсюда следует, что для использования методов второго порядка необходимым условием является дважды дифференцируемость . Центральное место среди методов второго порядка занимает метод Ньютона. Этот метод основан на квадратичной аппроксимации . Матрица вторых производных должна быть невырожденной.

Пусть -k - е приближение к точке минимума. Покажем, как, зная его, можно получить следующее приближение .

Разложим в ряд Тейлора в окрестности точки , оставляя члены разложения не выше второго:

.

В этой формуле использовано традиционное обозначение скалярного произведения векторов a и b как (a,b).

- матрица вторых производных , вычисленных в приближении .

Разложение в ряд Тейлора используется для того, чтобы через него определить следующее приближение как точку минимума , удовлетворяющую соотношению

или

,

откуда

Такая формула носит название формулы Ньютона.

Если начальное приближение выбрано достаточно близко к точке минимума, а - сильно выпуклая функция, метод Ньютона будет сходится с квадратичной скоростью сходимости, то есть

Пример.

Найти точку минимума с точностью .

Решение.

По критерию Сильвестра матрица является положительно определенной.

Напомним, что согласно критерию Сильвестра матрица положительна определена, если , а также определители всех миноров второго, ...., n - го порядка, окаймляющих этот элемент положительны.

		..................
		..................
.......................	.........................	.........................	..........................
		..................

Для этой задачи расчетная формула метода Ньютона будет иметь вид:

Введем критерии остановки:

В качестве начального приближения возьмем

Делаем первую итерацию по формуле Ньютона:

Проверяем критерий остановки:

следовательно, необходимо продолжить вычисления.

Делаем вторую итерацию по методу Ньютона:

Второе приближение совпало с первым, кроме того,

то есть выполнены все итерации остановки и решением поставленной задачи будет

Можно показать, что для любой квадратичной функции с положительно определенной матрицей вторых производных метод Ньютона дает точное решение независимо от начального приближения за одну итерацию. На рисунке 2.1 представлена блок-схема метода Ньютона. Итак, метод Ньютона как метод второго порядка имеет быструю сходимость, если начальное приближение близко к точке минимума, однако, он может работать плохо или даже отказать вдали от точки минимума. Нелегкой задачей является процедура нахождения матрицы вторых производных. Обычно метод Ньютона используется на заключительном этапе, когда на начальном этапе работают другие методы. На практике находят широкое применение модификации метода Ньютона, направленные на то, чтобы, сохраняя основное достоинство метода - его быструю сходимость, уменьшить трудоемкость и ослабить требования на выбор начального приближения.

Вот некоторые виды модификаций:

• метод Ньютона с регулировкой шага:

  

  Выбор производится либо из условия минимизации функции вдоль выбранного направления, либо путем дробления шага, обеспечивающего монотонное убывание , что обеспечивает сходимость при любой начальной точке;

• пересчет матрицы вторых производных производить не на каждом шаге.

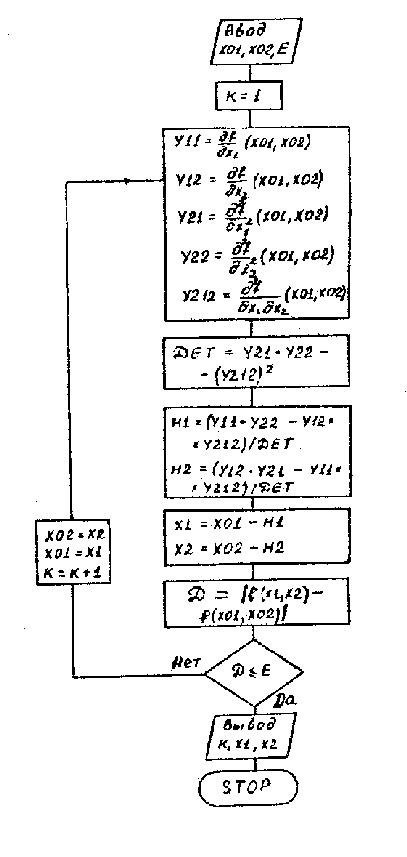
Рисунок 4.2.1

Блок - схема метода Ньютона.