
Лабораторные работы / LAB7
.RTF№7.Оптимизация системы обслуживания упорядоченных требований.
Лабораторная работа № 7
Тема: Оптимизация системы обслуживания упорядоченных
требований
Цель работы: Изучение и практическое применение алгоритма составления оптимального расписания обслуживания упорядоченных требований.
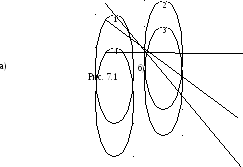
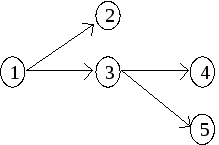
Многие задачи планирования и управления требуют упорядочивания во времени фиксированной системы ресурсов для выполнения определённой совокупности работ. При этом часто выполняемые работы не являются независимыми, ту или иную работу оказывается возможным осуществить только после окончания выполнения других работ. Средством графического представления взаимосвязи во времени выполнения отдельных работ являются различные типы сетевых графиков. Мы будем использовать сетевые графики в форме “вершины-работы”, состоящие из последовательности выполнения работ (см. Рис. 7.1).


Пусть
задано упорядоченное с помощью сетевого
графика множество
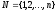 работ (требований), которые необходимо
обслужить на одном обрабатывающем
приборе (станок, ЭВМ и т. п.) начиная
обслуживание в момент
работ (требований), которые необходимо
обслужить на одном обрабатывающем
приборе (станок, ЭВМ и т. п.) начиная
обслуживание в момент
 .
Известны времена
.
Известны времена
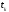 обслуживания всех требований. Одновременно
прибор может обслуживать не более одного
требования. Каждому требованию
обслуживания всех требований. Одновременно
прибор может обслуживать не более одного
требования. Каждому требованию
 сопоставлена функция
сопоставлена функция
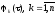 -
штраф, который необходимо заплатить,
если обработка k-го
требования завершится в момент
-
штраф, который необходимо заплатить,
если обработка k-го
требования завершится в момент
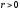 .
Качество расписания
.
Качество расписания
 будем оценивать функцией суммарного
штрафа
будем оценивать функцией суммарного
штрафа
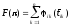
Здесь
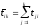 -
время окончания обслуживания k-го
требования. Поставим задачи отыскания
подстановки (расписания)
-
время окончания обслуживания k-го
требования. Поставим задачи отыскания
подстановки (расписания)
 ,
согласующейся с заданным сетевым
графиком и доставляющей минимум функции
,
согласующейся с заданным сетевым
графиком и доставляющей минимум функции
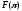 .
.
Введём
следующие определения. Множество
 будем называть допустимым, если не
существует таких элементов (работ)
будем называть допустимым, если не
существует таких элементов (работ) и
и
 ,
что
,
что
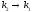 ,
так как работа
,
так как работа
 опирается на работу
опирается на работу
 .
На рис. 7.1 а) допустимыми множествами
являются {1}, {1,2}, {1,2,3}, {1,2,4}, {1,2,3,4}. Множество
{2,4} не является допустимым, так как
работа 2 опирается на работу 1, не
принадлежащую данному множеству.
.
На рис. 7.1 а) допустимыми множествами
являются {1}, {1,2}, {1,2,3}, {1,2,4}, {1,2,3,4}. Множество
{2,4} не является допустимым, так как
работа 2 опирается на работу 1, не
принадлежащую данному множеству.
Элемент
 назовём максимальным
элементом множества Q,
если не существует такого
назовём максимальным
элементом множества Q,
если не существует такого
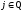 ,
что
,
что
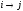 .
Множество всех максимальных элементов
Q
обозначим
.
Множество всех максимальных элементов
Q
обозначим
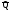 .
Например , для сетевого графика рис. 7.1
а) Q=3,4,
где
.
Например , для сетевого графика рис. 7.1
а) Q=3,4,
где
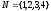 .
.
Пусть
Q
произвольное допустимое множество.
Рассмотрим всевозможные согласованные
с сетевым графиком последовательности
обработки требований
 .
Обозначим за
.
Обозначим за
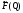 наименьший суммарный штраф, соответствующий
всем этим последовательностям. Положим
наименьший суммарный штраф, соответствующий
всем этим последовательностям. Положим
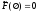 .
Заметим, что
.
Заметим, что
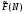 есть искомый минимальный суммарный
штраф за обработку всех требований
есть искомый минимальный суммарный
штраф за обработку всех требований
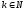 .
Имеет место рекуррентное соотношение
.
Имеет место рекуррентное соотношение
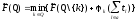 (7.1)
(7.1)
Соотношение (7.1) лежит в основе следующего алгоритма построения оптимального расписания.
Алгоритм.
1.Полагаем
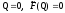 .
.
2.Пусть
уже рассмотрены все допустимые множестваQ,
состоящие из (m-1)
элементов. На m-м
шаге выделяются все допустимые множества,
состоящие из m
элементов, и для каждого из них с
использованием (7.1) находится величина
 ,
которая заносится в таблицу (см. Пример)
вместе с тем номером k,
для которого достигается минимум в
(7.1).
,
которая заносится в таблицу (см. Пример)
вместе с тем номером k,
для которого достигается минимум в
(7.1).
3.Пусть
рассмотрены все допустимые множества
Q,
состоящие из
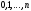 элементов, и для каждого из них найдены
элементов, и для каждого из них найдены
 и значения k,
доставляющие минимум в (7.1). Если при Q=N
значение
и значения k,
доставляющие минимум в (7.1). Если при Q=N
значение
 ,
полагаем
,
полагаем
 и исключаем элемент
и исключаем элемент
 из
дальнейших рассуждений. Рассматриваем
множество
из
дальнейших рассуждений. Рассматриваем
множество
 .
Если ему соответствует
.
Если ему соответствует
 ,
полагаем
,
полагаем
 .
.
Продолжая
таким образом, получим последовательность
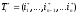 ,
которая и задаёт оптимальное расписание.
,
которая и задаёт оптимальное расписание.
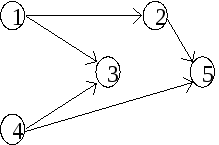
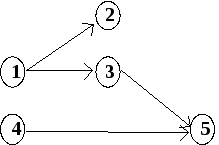
Пример:
Множество работ
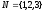 упорядочено сетевым графиком
упорядочено сетевым графиком


1
2
3
Времена выполнения отдельных работ и функций штрафа заданы таблицей
|
|
1 |
2 |
3 |
|
|
2 |
4 |
1 |
|
|
|
|
|
Решение: Результаты работы алгоритма представлены в следующей таблице
|
|
Q |
|
|
|
0 |
0 |
0 |
- |
|
1 |
1 3 |
4 6 |
1 3 |
|
2 |
1,2 1,3 |
17 14 |
2 1 |
|
3 |
1,2,3 |
29 |
2 |
-
{1}
 {3}
{3}

-
{1,2}
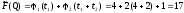 {1,3}
{1,3}
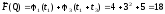 {3,1}
{3,1}
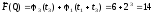

-
{1,2,3}

{3,1,2}

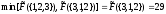
Поскольку
для
 значение
значение
 ,
то в оптимальном расписании
,
то в оптимальном расписании
 .
Далее, для
.
Далее, для
 величина
величина
 ,
следовательно,
,
следовательно,
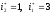 .
Окончательно получаем оптимальное
расписание
.
Окончательно получаем оптимальное
расписание
 .
При этом минимальный суммарный штраф
.
При этом минимальный суммарный штраф
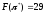 .
.
Задание
к лабораторной работе № 7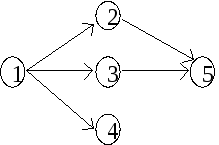
|
k |
1 |
2 |
3 |
4 |
5 |
|
tk |
2 |
3 |
1 |
3 |
2 |
|
k(t) |
2t-2+3 |
3t-5 |
2t2-3t+4 |
t-1 |
t2-t+4 |
1)
2)
|
k |
1 |
2 |
3 |
4 |
5 |
||||
|
tk |
3 |
1 |
1 |
2 |
2 |
||||
|
k(t) |
max (0,t–4) |
3t+2 |
2t+1–4 |
t2+t–1 |
2t |
||||
|
k |
1 |
2 |
3 |
4 |
5 |
||||
|
tk |
2 |
3 |
2 |
2 |
1 |
||||
|
k(t) |
3t+1 |
t2–5 |
2t–3t+4 |
3t–1 |
max (t+2,7) |
||||
3)
|
k |
1 |
2 |
3 |
4 |
5 |
|
tk |
2 |
1 |
3 |
4 |
2 |
|
k(t) |
2t+1 |
t2–1 |
2t–2 |
max (0,t–10) |
t2+t |
4)
5)
|
k |
1 |
2 |
3 |
4 |
5 |
|
tk |
1 |
3 |
2 |
3 |
2 |
|
k(t) |
2t–2 |
t–3 |
2t–3 |
t2+4t–4 |
t2–t |
6)

|
k |
1 |
2 |
3 |
4 |
5 |
|
tk |
3 |
1 |
2 |
1 |
2 |
|
k(t) |
2t–1 |
t2–1 |
2t-1–4 |
t3+1 |
t+1 |

7)






|
k |
1 |
2 |
3 |
4 |
5 |
|
tk |
1 |
2 |
2 |
1 |
3 |
|
k(t) |
3t–1 |
2t+1–1 |
t2+3t–4 |
t3–1 |
4t+1 |
8)
|
k |
1 |
2 |
3 |
4 |
5 |
|
tk |
1 |
3 |
2 |
1 |
2 |
|
k(t) |
2t-1–2 |
2t+1–1 |
33–2t |
2t–1 |
t2+1 |
9)
|
k |
1 |
2 |
3 |
4 |
5 |
|
tk |
2 |
3 |
2 |
2 |
1 |
|
k(t) |
t2+2t–4 |
2t+3 |
max (t–4,0) |
2t–1 |
t2–t+4 |
10)






|
k |
1 |
2 |
3 |
4 |
5 |
|
tk |
3 |
1 |
1 |
2 |
2 |
|
k(t) |
2t+1 |
t2 |
t2–2t+2 |
t3–5 |
t–2 |
11)
|
k |
1 |
2 |
3 |
4 |
5 |
|
tk |
3 |
1 |
2 |
1 |
2 |
|
k(t) |
2t-1–1 |
2t2–2 |
2t+1 |
t2–1 |
3t–2 |
12)






|
k |
1 |
2 |
3 |
4 |
5 |
|
tk |
1 |
3 |
2 |
1 |
2 |
|
k(t) |
2t |
t–3 |
2t2–2 |
2t-1+1 |
4t–5 |
13)





|
k |
1 |
2 |
3 |
4 |
5 |
|
tk |
1 |
3 |
2 |
3 |
1 |
|
k(t) |
2t+2–6 |
t3–7 |
t2+2t–6 |
2t |
t–5 |
14)






|
k |
1 |
2 |
3 |
4 |
5 |
|
tk |
1 |
3 |
1 |
3 |
1 |
|
k(t) |
2t |
t2+t |
max (t–6,0) |
2t+1 |
t2 |
15)





|
k |
1 |
2 |
3 |
4 |
5 |
|
tk |
1 |
1 |
2 |
1 |
3 |
|
k(t) |
2t+1 |
t2–1 |
2t2–5 |
max (t+3,7) |
2t–3 |
16)






|
k |
1 |
2 |
3 |
4 |
5 |
|
tk |
2 |
1 |
2 |
1 |
2 |
|
k(t) |
2t–1 |
6–max (t–3,1) |
t2+1 |
t3+2 |
3t+2 |
17)





|
k |
1 |
2 |
3 |
4 |
5 |
|
tk |
3 |
1 |
2 |
1 |
3 |
|
k(t) |
2t+1–2 |
5t–6 |
max (6–t,0) |
t3+2 |
3t2–4t+2 |
18)





|
k |
1 |
2 |
3 |
4 |
5 |
|
tk |
1 |
2 |
1 |
1 |
3 |
|
k(t) |
2t-1 |
t3–t2+4t |
2t+3–1 |
5t–6 |
t3–2t+4 |
19)





|
k |
1 |
2 |
3 |
4 |
5 |
|
tk |
1 |
2 |
1 |
2 |
3 |
|
k(t) |
t2+t–1 |
2t+3 |
2t+2 |
max(0,5t–6) |
t2–t+4 |
20)






|
k |
1 |
2 |
3 |
4 |
5 |
|
tk |
1 |
2 |
1 |
3 |
1 |
|
k(t) |
2t2–1 |
2t+1–4 |
t3+2 |
t+1 |
2t–t |
