Практическая работа №2. Вычисление пределов функции. Применение производной к исследованию функции. Неопределенный интеграл. Нахождение неопределенных интегралов различными методами.

Цель работы. Сформировать навыки вычисления пределов последовательностей и пределов функций. Сформировать умение находить производные сложных функций, усвоить геометрический и физический смысл производной. Сформировать навыки нахождения неопределенных интегралов различными методами

Порядок выполнения работы:

1. Повторите теоретические положения по теме и записать определение, формулы расчета и т.п.

2. Выполните задание, согласно своего варианта. Исходные данные возьмите в приложении.

3. Сделайте выводы по результатам работы

Вариант1.

Задание 1. Раскрыть неопределённость   и найти предел  .

Решение.

Здесь старшая степень переменной n равна 2. Поэтому почленно делим числитель и знаменатель на  :

.

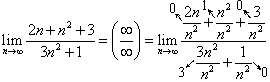Получаем ответ: предел данной функции при переменной, стремящейся к бесконечности, равен  .

Задание 2. Исследовать функцию

и построить её график.

Решение.

1. Область определения функции – вся числовая прямая. Множеством значений данной функции, как и всякой показательной функции, служит интервал ]0, +∞[. Поэтому график функции расположен выше оси Ox,

2. Напомним: из школьного курса известно, что функция y = f(x) называется чётной, если

 для всех x, принадлежащих области определения функции.

.

График чётной функции симметричен относительно оси Oy, так как, по определению, вместе с любой своей точкой (x; y) он содержит и точку (-x; y).

Функция y = f(x) называется нечётной, если

 для всех x, принадлежащих области определения функции.

График нечётной функции симметричен относительно начала координат, так как, по определению, вместе с любой своей точкой (x; y) он содержит и точку (-x; -y).

Наша исследуемая функция чётная, так как

её график симметричен относительно оси Oy. Поэтому исследование можно выполнять только для ]0, +∞[.

3. Вертикальных асимптот у графика нет, поскольку функция непрерывна на всей числовой прямой. Горизонтальной асимптотой является ось Ox, так как

Поскольку кривая имеет двустороннюю горизонтальную асимптоту y = 0, у неё не может быть наклонных асиптот.

4. Находим

Из уравнения

имеем

Так как  при переходе через значение x = 0 меняет знак с плюса на минус, то функция в точке x = 0 переходит от возрастания к убыванию, а (0; 1) – точка максимума. Касательная к кривой в этой точке горизонтальна, поскольку

5. Находим

Из уравнения

получаем

т.е.

Учитывая чётность функции, исследуем знаки  в окрестности только точки

Следовательно, при x = 1 кривая меняет выпуклость на вогнутость. Так как

то

точка перегиба кривой. Угловой коэффициент касательной в кривой в этой точке

поэтому в точке перегиба касательная образует с осью Ox тупой угол.

6. График не пересекает оси Ox, поскольку он расположен выше неё. Найдём точки пересечения кривой с осью Oy: полагая x = 0, имеем

Тем самым получим точку (0; 1) графика, которая совпадает с точкой максимума.

7. Составим сводную таблицу исследования функции, куда внесём все характерные точки и интервалы между ними. Учитывая чётность функции, получаем следующую таблицу:

				Особенности графика
[-1, 0[	+	-	Возрастает	Выпуклый
0	0	-	1	(0; 1) – точка максимума
]0, 1[	-	-	Убывает	Выпуклый
1	-	0		- точка перегиба, образует с осью Ox тупой угол
]1, +∞[	-	+	Убывает	Вогнутый
+∞	-	+		y = 0 – горизонтальная асимптота

  

8. Используя результаты исследования, строим график функции

Задание 3. Найти неопределённый интеграл методом замены переменной:

Решение. Положим x – 1 = t ; тогда x = t + 1. Отсюда dx = dt . По формуле (1)

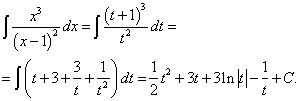
Возвращаясь к переменной x, окончательно получаем

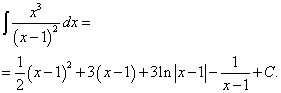
Задание 4. Найти неопределённый интеграл:

.

Решение. Пусть  ,  .

Логарифм присутствует в квадрате. Это значит, что его нужно дифференцировать как сложную функцию. Находим ,  .

Применяя формулу интегрирования по частям, получаем:

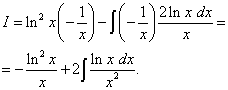
Второй интеграл вновь находим по частям.

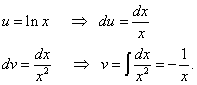
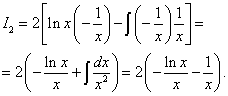
Находим изначальный интеграл:

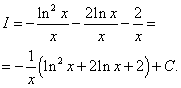
Вывод. В ходе выполнения этой работы я научился вычислять пределы функции, проводить исследование функций с помощь производной. Закрепил навыки нахождения интегралов различными методами.

Практическая работа №2. Вычисление пределов функции. Применение производной к исследованию функции. Неопределенный интеграл. Нахождение неопределенных интегралов различными методами.

Цель работы. Сформировать навыки вычисления пределов последовательностей и пределов функций. Сформировать умение находить производные сложных функций, усвоить геометрический и физический смысл производной. Сформировать навыки нахождения неопределенных интегралов различными методами

Порядок выполнения работы:

1. Повторите теоретические положения по теме и записать определение, формулы расчета и т.П.

2. Выполните задание, согласно своего варианта. Исходные данные возьмите в приложении.

3.Сделайте выводы по результатам работы

Вариант 2.

Задание 1. Раскрыть неопределённость   и найти предел  .

Решение. Здесь старшая степень переменной x равна 1. Поэтому почленно делим числитель и знаменатель на x:

.

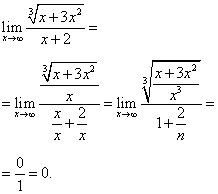Задание 2. Исследовать функцию   и построить ее график.

Решение. 1) Область определения функции.

2) Четность, нечетность.

Функция общего вида.

3) Точки пересечения с осями.

а) с осью   :

то есть точки 

б) с осью   : в данной точке функция неопределенна.

4) Асимптоты.

а) вертикальные: прямые   и   - вертикальные асимптоты.

б) горизонтальные асимптоты:

то есть прямая   - горизонтальная асимптота.

в) наклонные асимптоты   :

Таким образом, наклонных асимптот нет.

5) Критические точки функции, интервалы возрастания, убывания.

Найдем точки, в которых первая производная равна нулю или не существует:   для любого   из области определения функции;   не существует при   и   .

Таким образом, функция убывает на всей области существования. Точек экстремума нет.

6) Точки перегиба, интервалы выпуклости, вогнутости.

Найдем точки, в которых вторая производная равна нулю или не существует:   ; при  и   вторая производная не существует.

Таким образом, на промежутках   и   функция вогнута, а на промежутках   и   - выпукла. Так как при переходе через точку   вторая производная поменяла знак, то эта точка является точкой перегиба.

7) Эскиз графика.

Задание 3. Найти неопределённый интеграл методом замены переменной:

.

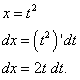Решение. Положим  . Отсюда  .  По формуле (1)

.

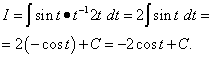Возвращаясь к переменной x, окончательно получаем

Задание 4. Найти неопределённый интеграл методом интегрирования по частям:

.

Решение. Пусть  ,  .

Тогда  ,  .

Применяя формулу интегрирования по частям, получаем:

Второй интеграл находим методом замены переменной.

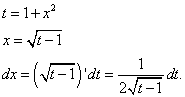
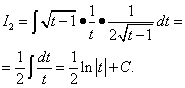
Возвращаясь к переменной x, получаем

.

Находим изначальный интеграл:

Вывод. В ходе выполнения этой работы я научился вычислять пределы функции, проводить исследование функций с помощь производной. Закрепил навыки нахождения интегралов различными методами.

Практическая работа №2. Вычисление пределов функции. Применение производной к исследованию функции. Неопределенный интеграл. Нахождение неопределенных интегралов различными методами.

Цель работы. Сформировать навыки вычисления пределов последовательностей и пределов функций. Сформировать умение находить производные сложных функций, усвоить геометрический и физический смысл производной. Сформировать навыки нахождения неопределенных интегралов различными методами

Порядок выполнения работы: