
- •Основи теорії кіл, сигналів та процесів в системах технічного захисту інформації
- •Поля і хвилі в системах технічного захисту інформації
- •Методи та засоби захисту інформації
- •Схемотехніка пристроїв технічного захисту інформації
- •Засоби приймання та обробки інформації в системах технічного захисту інформації
- •Засоби передавання інформації в системах тзі
Основи теорії кіл, сигналів та процесів в системах технічного захисту інформації
Запитання |
Визначити поняття «електричний струм» |
Відповідь |
Вiдношення потенцiйної енергiї w, яку має заряд q, що перебуває в данiй точцi, до цього заряду |
Відповідь |
Явище напрямленого руху носiїв зарядiв (заряджених часток) |
Відповідь |
Явище змiни електромагнiтного поля в часi |
Відповідь |
Різниця електричних потенціалів двох точок |
Відповідь |
Скалярна величина, що дорівнює похідній за часом від електричного заряду, який переноситься носіями заряду через дану поверхню |
Запитання |
Визначити поняття «схема кола» |
Відповідь |
Графічне зображення кола |
Відповідь |
Кресленик (рисунок), який відображає взаємозв’язок елементів кола |
Відповідь |
Умовне графічне подання кола |
Відповідь |
Графічна модель електричного кола, що зображує його за допомогою ідеальних елементів |
Відповідь |
Подання кола у вигляді сукупності умовних графічних зображень елементів |
Запитання |
Сформулювати закон Ома |
Відповідь |
Величина струму в замкненому електричному колi прямо пропорційна електрорушiйнiй силі та обернено пропорційна опору кола |
Відповідь |
Величина струму в замкненому електричному колi прямо пропорційна опору кола i обернено пропорційна електрорушiйнiй силі |
Відповідь |
Алгебраїчна сума ЕРС, дiючих у контурі схеми, дорiвнює алгебраїчний сумі спадів напруг на всiх дiлянках цього контуру в будь-який момент часу |
Відповідь |
Алгебраїчна сума струмiв, якi збiгаються у вузлi, в будь-який момент часу дорiвнює нулю |
Відповідь |
Величина струму в замкненому електричному колi прямо пропорцiйна електрорушiйнiй силi та обернено пропорцiйна провідності кола |
Запитання |
Сформулювати перший закон Кірхгофа |
Відповідь |
Сума струмiв, якi входять у вузол, дорiвнює сумi струмiв, що виходять із вузла |
Відповідь |
Величина струму в замкненому електричному колi прямо пропорцiйна електрорушiйнiй силi i обернено пропорцiйна опору кола |
Відповідь |
Алгебраїчна сума ЕРС, дiючих у контурi схеми, дорiвнює алгебраїчнiй сумi спадів напруг на всiх дiлянках цього контуру в будь-який момент часу |
Відповідь |
Алгебраїчна сума струмiв, якi сходяться у вузлi, в будь-який момент часу дорiвнює нулю |
Відповідь |
Сума ЕРС, дiючих у контурi схеми, дорiвнює сумi спадів напруг на всiх дiлянках цього контуру в будь-який момент часу |
Запитання |
Сформулювати другий закон Кірхгофа |
Відповідь |
Сума спадiв напруг у контурi дорiвнює нулю |
Відповідь |
Алгебраїчна сума струмiв, якi збiгаються у вузлi, в будь-який момент часу дорiвнює нулю |
Відповідь |
Алгебраїчна сума ЕРС, дiючих у контурi схеми, дорiвнює алгебраїчнiй сумi спадів напруг на всiх пасивних дiлянках цього контуру в будь-який момент часу |
Відповідь |
Величина струму в замкненому електричному колi прямо пропорцiйна електрорушiйнiй силi та обернено пропорцiйна опору кола |
Відповідь |
Cума ЕРС, дiючих у контурi схеми, дорiвнює сумi спадів напруг на всiх дiлянках цього контуру в будь-який момент часу |
Запитання |
Скільки незалежних рівнянь складають на підставі першого закону Кірхгофа, якщо у колі M вузлів і N віток? |
Відповідь |
M – N |
Відповідь |
M + N |
Відповідь |
M – 1 |
Відповідь |
M + 1 |
Відповідь |
M – N +1 |
Запитання |
Який
вигляд має аналітичний вираз синусоїдного
струму
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
Яке
співвідношення існує між діючим
значенням синусоїдного струму
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
Яке
значення має комплексна амплітуда
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
Який вид резонанса спостерігається у паралельному контурі? |
Відповідь |
Резонанс опорів |
Відповідь |
Резонанс струмів |
Відповідь |
Резонанс напруг |
Відповідь |
Резонанс провідностей |
Відповідь |
Резонанс фаз |
Запитання |
Яка формула визначає резонансний опір послідовного контуру? |
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
У послідовному резонансному контурі умовою резонанса є: |
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
Яка
формула визначає добротність контуру
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
Назвати умови виникнення перехідних процесів |
Відповідь |
Наявність у колі реактивних елементів |
Відповідь |
Наявність процесу комутації |
Відповідь |
Наявність джерел енергії |
Відповідь |
Наявність джерел коливань довільної форми |
Відповідь |
Різка зміна параметрів або структури кола, що містить реактивні елементи |
Запитання |
Які формули виражають закони комутації? |
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
;
|
Відповідь |
; |
Запитання |
Який
зв’язок існує між практичною тривалістю
перехідного процесу і сталою часу
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
Який закон описує змінювання вільної складової відгуку у колі першого порядку? |
Відповідь |
Гіперболічний |
Відповідь |
Експоненційний |
Відповідь |
Логарифмічний |
Відповідь |
Параболічний |
Відповідь |
Синусоїдний |
Запитання |
Яка
формула визначає струм
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
Визначити
перехідну характеристику кола, якщо
дія
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
Яка
формула встановлює зв’язок між
перехідною характеристикою
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
Якщо
струм двополюсника дорівнює
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
Яка формула визначає комплексний опір кола?
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
Яка
формула визначає АЧХ кола, якщо дія –
напруга
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
КПФ
кола
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
Обчислити
сталу часу кола, якщо
|
Відповідь |
1 мс |
Відповідь |
1,75 мс |
Відповідь |
3,75 мс |
Відповідь |
2,5 мс |
Відповідь |
3,15 мс |
Запитання |
Обчислити
сталу часу R, L кола, якщо
|
Відповідь |
1 мс |
Відповідь |
2 мс |
Відповідь |
0,5 мс |
Відповідь |
2 нс |
Відповідь |
2 мкс |
Запитання |
Знайти
|
Відповідь |
0,66 мА |
Відповідь |
0,2 мА |
Відповідь |
0,5 мА |
Відповідь |
0,4 мА |
Відповідь |
1 мА |
Запитання |
Яка
формула визначає
|
Відповідь |
|
Відповідь |
|
Відповідь |
0 |
Відповідь |
|
Відповідь |
|
Запитання |
Знайти
струм
. |
Відповідь |
5 мА |
Відповідь |
4,5 мА |
Відповідь |
7,5 мА |
Відповідь |
2,5 мА |
Відповідь |
8,5 мА |
Запитання |
Визначити
еквівалентний опір кола відносно
точок 1-2, якщо
|
Відповідь |
3 кОм |
Відповідь |
4 кОм |
Відповідь |
5 кОм |
Відповідь |
6 кОм |
Відповідь |
11 кОм |
Запитання |
Графік якого сигналу зображено на рисунку?
|
Відповідь |
Неперервний |
Відповідь |
Дискретний |
Відповідь |
Квантований |
Відповідь |
Цифровий |
Відповідь |
Періодичний |
Запитання |
Коефіцієнти
узагальненого ряду Фур’є
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
Яка
з наступних форм запису ряду Фур’є
для довільного періодичного сигналу
з періодом
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
Амплітудно-частотний спектр якого сигналу зображено на рисунку?
|
Відповідь |
Поодинокий відеоімпульс |
Відповідь |
Періодична послідовність відеоімпульсів |
Відповідь |
Поодинокий радіоімпульс |
Відповідь |
Гармонічне коливання |
Відповідь |
Даний спектр не відповідає жодному з каузальних, тобто таких, що можна реалізувати фізично, сигналів |
Запитання |
За
допомогою якого з наступних виразів
можна розрахувати спектральну густину
неперіодичного сигналу
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
Задано
сигнал
,
якому відповідає спектральна густина
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
Щоб
відновити неперервний сигнал
з дискретного
|
Відповідь |
фільтр низьких частот |
Відповідь |
фільтр високих частот |
Відповідь |
смуговий фільтр |
Відповідь |
режекторний фільтр |
Відповідь |
цифро-аналоговий перетворювач |
Запитання |
Сигнал
зветься вузькосмуговим, якщо його
спектральна густина відмінна від нуля
лише в межах смуги частот
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
Яка з наступних властивостей узагальненого ряду Фур’є є вірною? |
Відповідь |
Коефіцієнти узагальненого ряду Фур’є не складають оптимальний за критерієм мінімуму енергії (потужності) похибки набір |
Відповідь |
Коефіцієнти узагальненого ряду Фур’є залежать один від одного, тобто кожен з коефіцієнтів ряду обчислюється залежно від усіх останніх |
Відповідь |
Якщо сигнал
|
Відповідь |
Для ряду Фур`є виконуються рівності Бесселя та Парсеваля |
Відповідь |
Якщо базисна
система функцій є повною для даного
класу сигналів, то при кількості членів
ряду
|
Запитання |
Яка з наступних властивостей спектрів періодичних сигналів є вірною? |
Відповідь |
Амплітудно-частотний спектр повністю визначає відображення періодичного сигналу в частотній області |
Відповідь |
Спектр періодичного
сигналу дискретний. Він складається
з окремих ліній на відповідних частотах
|
Відповідь |
Якщо періодичний
сигнал
є дійсною й парною функцією часу, то
дійсна частина коефіцієнтів ряду
Фур`є
|
Відповідь |
Якщо періодичний
сигнал
є дійсною і непарною функцією часу,
то уявна частина коефіцієнтів ряду
Фур`є
дорівнює нулю, а фази коефіцієнтів
ряду Фур`є
можуть набувати лише двох значень:
|
Відповідь |
Середня потужність періодичного сигналу завжди є меншою за потужність відповідного цьому сигналу ряду Фур`є |
Запитання |
Задано
сигнал
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
Задано
сигнал
,
який подається на лінійне коло з
постійними параметрами, що має імпульсну
характеристику
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
Який
з наступних виразів є умовою каузальності,
тобто умовою фізичної реалізації,
радіотехнічного кола з коефіцієнтом
передачі
та імпульсною характеристикою
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
Який з наступних виразів є умовою лінійного радіотехнічного кола, яке не вносить спотворень, з коефіцієнтом передачі та імпульсною характеристикою ? |
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
Ідеальний фільтр низьких частот має наступну амплітудно-частотну характеристику: |
Відповідь |
|
Відповідь |
|
Відповідь |
причому
|
Відповідь |
причому |
Відповідь |
|
Запитання |
Довільний сигнал задано на скінченному інтервалі часу . За допомогою якого виразу можна визначити енергію сигналу ? |
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
Яка з
наступних властивостей автокореляційної
функції (АКФ)
|
Відповідь |
АКФ дійснозначного
сигналу зі скінченною енергією є
дійснозначною непарною функцією,
тобто
|
Відповідь |
Значення АКФ
дійснозначного сигналу зі скінченною
енергією при
|
Відповідь |
АКФ сигналу зі
скінченною енергією і тривалістю
набуває максимального значення при
|
Відповідь |
АКФ сигналу зі скінченною енергією та його спектральна густина енергії пов’язані парою перетворень
|
Відповідь |
АКФ дійснозначного
сигналу зі скінченною енергією є
додатною функцією, тобто
|
Запитання |
Який
з наступних виразів є умовою
ортогональності на інтервалі часу
двох сигналів
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
Яким чином при інтегруванні сигналу змінюється його спектр в околі нульової частоти (НулЧ), в області низьких частот (НЧ) та в області високих частот (ВЧ)? |
Відповідь |
Співвідношення між амплітудами спектральних складових не змінюються |
Відповідь |
Амплітуди НулЧ зменшуються, амплітуди НЧ зменшуються, амплітуди ВЧ зменшуються |
Відповідь |
Амплітуди НулЧ зростають, амплітуди НЧ зростають, амплітуди ВЧ зростають |
Відповідь |
Амплітуди НулЧ зменшуються, амплітуди НЧ зростають, амплітуди ВЧ зростають |
Відповідь |
Амплітуди НулЧ зростають, амплітуди НЧ зменшуються, амплітуди ВЧ зменшуються |
Запитання |
Що змінюється в спектрі сигналу при зсуві його у часі |
Відповідь |
Уявна частина спектру |
Відповідь |
Дійсна частина спектру |
Відповідь |
Модуль спектру (амплітудно-частотний спектр) |
Відповідь |
Аргумент спектру (фазо-частотний спектр) |
Відповідь |
Змінюються усі спектральні складові |
Запитання |
Що не змінюється в спектрі сигналу при зміні його амплітуди |
Відповідь |
Уявна частина спектру |
Відповідь |
Дійсна частина спектру |
Відповідь |
Модуль спектру (амплітудно-частотний спектр) |
Відповідь |
Аргумент спектру (фазо-частотний спектр) |
Відповідь |
Змінюються усі спектральні складові |
Запитання |
Яка з наступних властивостей коливань з амплітудною модуляцією є вірною? |
Відповідь |
Якщо ширина спектру
модулюючого коливання дорівнює
|
Відповідь |
Амплітуди бічних складових у спектрі тонального АМ коливання мають парну симетрію |
Відповідь |
Тональні АМ коливання мають значно більшу ширину спектру, ніж тональні ЧМ і ФМ коливання |
Відповідь |
Тональні АМ коливання більш енергетично вигідні, ніж тональні ЧМ і ФМ коливання, їх ККД може становити до 90% |
Відповідь |
Фази бічних складових у спектрі тонального АМ коливання мають парну симетрію |
Запитання |
Яка з наступних властивостей коливань з кутовою модуляцією не є вірною? |
Відповідь |
ЧМ коливання для
модулюючого сигналу
|
Відповідь |
Зростання девіації частоти для коливання з ЧМ призводить до зростання ширини його спектру |
Відповідь |
Якщо ширина спектру
модулюючого коливання дорівнює
,
то спектр тонального ФМ коливання має
ширину
|
Відповідь |
ФМ коливання для
модулюючого сигналу
можна отримати за допомогою частотного
модулятора, якщо подати на його вхід
коливання
|
Відповідь |
Сигнали з фазовою і частотною модуляцією більш перешкодостійкі, ніж сигнали з амплітудною модуляцією |
Запитання |
Який
з наступних виразів встановлює зв'язок
між спектром
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
Яке з наступних тверджень не є вірним? |
Відповідь |
Збільшення частоти дискретизації зменшує ступінь відмінності відновленого з дискретного і вихідного безперервного сигналів |
Відповідь |
Зменшення інтервалу дискретизації зменшує ступінь відмінності відновленого з дискретного і вихідного безперервного сигналів |
Відповідь |
Збільшення тривалості сигналів, за допомогою яких беруть вибірки, зменшує ступінь відмінності відновленого з дискретного і вихідного безперервного сигналів |
Відповідь |
Всі фізичні сигнали є сигналами з необмеженим спектром. Це призводить до того, що накладання копій спектра вихідного сигналу при формуванні спектра дискретного сигналу неминуче, що спотворює відновлений сигнал |
Відповідь |
При дискретизації реальних сигналів з'являються спотворення за рахунок скінченної кількості відліків за обмежений час тривалості сигналу, в той час як їх має бути нескінченно багато, бо обмеження спектру сигналу відповідає збільшенню його тривалості до нескінченності |
Запитання |
Якою операцією в частотній області відображується підсумовування сигналів та у часовій області? |
Відповідь |
Згорткою спектрів сигналів |
Відповідь |
Добутком спектрів сигналів |
Відповідь |
Сумою спектрів сигналів |
Відповідь |
Згорткою дійсних частин спектрів сигналів |
Відповідь |
Добутком дійсних частин спектрів сигналів |
Запитання |
Яким типом спектру відображається у частотній області сигнал, що можна реалізувати фізично |
Відповідь |
Скінченним |
Відповідь |
Періодичним |
Відповідь |
Дискретним |
Відповідь |
Нескінченним |
Відповідь |
Квантованим |
Запитання |
Розрахувати
потужність прмякутного відеоімпульсу
з амплітудою
та тривалістю
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
Графік
сигналу
|
Відповідь |
де
|
Відповідь |
де – одинична функція Хевісайда |
Відповідь |
де – одинична функція Хевісайда |
Відповідь |
де – одинична функція Хевісайда |
Відповідь |
де – одинична функція Хевісайда |
Запитання |
Графік
однотонального АМ коливання з
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
Лінійне
частотновибіркове коло охоплено
від’ємним зворотнім зв’язком. Як при
цьому зміняться максимальне значення
коефіцієнту передачі
|
Відповідь |
зросте, зменшиться. |
Відповідь |
зросте, зросте. |
Відповідь |
зменшиться, зменшиться. |
Відповідь |
зменшиться, зросте. |
Відповідь |
не зміниться, не зміниться. |
Запитання |
Амплітудно-частотний спектр сигналу зображено на рисунку. Тривалість сигналу було збільшено в 2 рази, який з наступних амплітудно-частотних спектрів буде відповідати новому сигналу?
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
Характеристика нелінійної системи має вигляд:
На систему діє коливання:
Знайти
амплітуду другої гармоніки сигналу
|
Відповідь |
0,25 В |
Відповідь |
0,50 B |
Відповідь |
0,75 B |
Відповідь |
1,25 B |
Відповідь |
1,75 B |
Запитання |
Чому дорівнює значення на нульовій частоті спектру сигналу, зображеного на рисунку?
|
Відповідь |
7 |
Відповідь |
5 |
Відповідь |
3 |
Відповідь |
4 |
Відповідь |
6 |
Запитання |
Спектр
сигналу
дорівнює нулю поза смугою
|
Відповідь |
200 Гц |
Відповідь |
1000 Гц |
Відповідь |
20 Гц |
Відповідь |
2000 Гц |
Відповідь |
10 Гц |
Запитання |
Який з наступних виразів відповідає спектру сигналу, зображеного на рисунку?
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
Однотональне
ЧМ коливання має такі параметри: несуча
частота
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
На якому рисунку зображено графік автокореляційної функції фізичного сигналу зі скінченною енергією? |
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
Визначити максимальну та мінімальну частоту модульованого сигналу
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
При впливі на нелінійний елемент гармонічної напруги кут відсікання струму становить
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Відповідь |
|
Запитання |
Скільки спектральних складових має однотональне АМ коливання
|
Відповідь |
3 |
Відповідь |
7 |
Відповідь |
4 |
Відповідь |
6 |
Відповідь |
5 |
Запитання |
На рисунку зображено амплітудно-частотний спектр сигналу, з якого беруться відліки з частотами 30, 40 і 60 Гц. Яка (або які) з трьох частот відліків відповідає теоремі відліків?
|
Відповідь |
40 Гц, 60 Гц |
Відповідь |
30 Гц, 40 Гц |
Відповідь |
60 Гц |
Відповідь |
30 Гц |
Відповідь |
40 Гц |

 ?
?




 та амплітудою
та амплітудою
 ?
?




 ,
що відповідає коливанню
,
що відповідає коливанню
 В?
В? В
В В
В
 В
В В
В В
В









 ?
?



 ;
;

 ;
;
 ;
;


 кола?
кола?




 на виході кола з перехідною характеристикою
на виході кола з перехідною характеристикою
 та імпульсною характеристикою
та імпульсною характеристикою
 ,
якщо на вході діє напруга
,
якщо на вході діє напруга
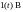 ?
?




 ,
а відгук –
,
а відгук –
 .
.





 та операторною передатною функцією
кола
та операторною передатною функцією
кола
 ?
?




 А,
а напруга на його затискачах
А,
а напруга на його затискачах
 В,
яке значення має комплексний опір
В,
яке значення має комплексний опір
 ?
? Ом
Ом Ом
Ом Ом
Ом Ом
Ом Ом
Ом





 ,
а відгук – напруга
,
а відгук – напруга
 ?
?





 .
Який вираз визначає ФЧХ, якщо
.
Який вираз визначає ФЧХ, якщо
 – індуктивний опір?
– індуктивний опір?




 ;
;
 ;
;
 ;
;
 .
.

 ;
;

 ,
якщо
,
якщо
 ;
;
 ;
;
;
;
 ;
;
 .
.

 ?
?





 ,
якщо
,
якщо
 ;
;
 ;
;
;
;
;
;
 .
.
 ;
;
 ;
;

 за умови
за умови
 розраховуються за виразом:
розраховуються за виразом:




 є вірною?
є вірною?





 ?
?





 ,
до того ж
,
до того ж
 при
при
 .
Відповідно до теореми Котельникова
такий сигнал можна представити
відліками миттєвих значень
.
Відповідно до теореми Котельникова
такий сигнал можна представити
відліками миттєвих значень
 ,
де інтервал дискретизації
,
де інтервал дискретизації
 визначається наступним чином:
визначається наступним чином:




 потрібно дискретний сигнал пропустити
через
потрібно дискретний сигнал пропустити
через в околі частот
в околі частот
 ,
причому виконується умова:
,
причому виконується умова:





 задано на скінченному інтервалі
задано на скінченному інтервалі
 ,
відповідний ряд Фур`є збігатиметься
до
цьому інтервалі. Поза цим інтервалом
ряд Фур`є збігається до сигналу, який
періодично продовжує сигнал
,
відповідний ряд Фур`є збігатиметься
до
цьому інтервалі. Поза цим інтервалом
ряд Фур`є збігається до сигналу, який
періодично продовжує сигнал
 відносна похибка апроксимації прямує
до одиниці
відносна похибка апроксимації прямує
до одиниці ,
де
,
де
 – частота першої гармоніки
– частота першої гармоніки дорівнює нулю, а фази коефіцієнтів
ряду Фур`є
можуть набувати лише двох значень:
дорівнює нулю, а фази коефіцієнтів
ряду Фур`є
можуть набувати лише двох значень:
 або
або

 або
або

 зі спектральною густиною
зі спектральною густиною
 ,
який подається на лінійне коло з
постійними параметрами, що має
коефіцієнт передачі
,
який подається на лінійне коло з
постійними параметрами, що має
коефіцієнт передачі
 .
За допомогою якого з наступних шляхів
можна визначити сигнал
.
За допомогою якого з наступних шляхів
можна визначити сигнал
 на виході кола?
на виході кола?





 .
За допомогою якого з наступних шляхів
можна визначити сигнал
на виході кола?
.
За допомогою якого з наступних шляхів
можна визначити сигнал
на виході кола?





 ?
? ,
якщо
,
якщо


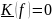 ,
якщо
,
якщо



 ,
де
,
де
 – деяка додатна константа,
– деяка додатна константа,
 – одинична функція Хевісайда
– одинична функція Хевісайда ,
де
– деяка додатна константа
,
де
– деяка додатна константа ,
де
– деяка додатна константа
,
де
– деяка додатна константа ,
де
– деяка додатна константа,
,
де
– деяка додатна константа,
 – одинична функція Хевісайда
– одинична функція Хевісайда ,
де
і
,
де
і
 –
деякі додатні константи
–
деякі додатні константи , де
– деяка додатна частота
, де
– деяка додатна частота , де
– деяка додатна частота
, де
– деяка додатна частота , де
і
, де
і
 – деякі додатні частоти,
– деякі додатні частоти,
 , де
і
– деякі додатні частоти,
, де
і
– деякі додатні частоти, , де
– деяка додатна частота
, де
– деяка додатна частота




 сигналу
є вірною?
сигналу
є вірною?
 дорівнює повній енергії сигналу, тобто
дорівнює повній енергії сигналу, тобто

 ,
тобто
,
тобто




 і
і
 з енергіями
з енергіями
 та
та
 відповідно?
відповідно?




 ,
то спектр АМ коливання має ширину
,
то спектр АМ коливання має ширину
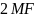 ,
де
,
де
 – індекс амплітудної модуляції
– індекс амплітудної модуляції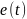 можна отримати за допомогою фазового
модулятора, якщо подати на його вхід
коливання
можна отримати за допомогою фазового
модулятора, якщо подати на його вхід
коливання

 ,
де
,
де
 – частота девіації
– частота девіації
 поодинокого імпульсу
та спектром
поодинокого імпульсу
та спектром
 періодичної послідовності імпульсів
з періодом слідування
?
періодичної послідовності імпульсів
з періодом слідування
? ,
де
,
де
 ,
,
 – ціле
– ціле ,
де
,
– ціле
,
де
,
– ціле ,
де
,
де
 ,
де
,
– ціле
,
де
,
– ціле ,
де
,
де
 .
.





 наведено на рисунку. Який з наступних
виразів є математичною моделлю сигналу?
наведено на рисунку. Який з наступних
виразів є математичною моделлю сигналу?

 ,
,
 – одинична функція Хевісайда
– одинична функція Хевісайда ,
,
 ,
,
 ,
,
 ,
,
 В
та
В
та
 В
наведено на рисунку. Чому дорівнюють
коефіцієнт модуляції
та амплітуда носійного коливання
В
наведено на рисунку. Чому дорівнюють
коефіцієнт модуляції
та амплітуда носійного коливання
 ?
?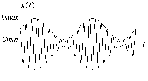
 ,
,
 B
B ,
,
 B
B ,
,
 B
B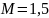 ,
B
,
B ,
B
,
B та ширина смуги пропускання
?
та ширина смуги пропускання
?





 ,
В.
,
В. ,
В.
,
В.

 Гц. Знайти частоту дискретизації для
сигналу
Гц. Знайти частоту дискретизації для
сигналу
 .
.





 МГц,
частота модулюючого гармонічного
сигналу
МГц,
частота модулюючого гармонічного
сигналу
 кГц.
В яких межах
кГц.
В яких межах
 змінюється миттєва частота цього
коливання, якщо індекс модуляції
змінюється миттєва частота цього
коливання, якщо індекс модуляції
 дорівнює 5?
дорівнює 5? МГц
МГц МГц
МГц МГц
МГц МГц
МГц МГц
МГц




 ,
В.
,
В. Гц,
Гц,
 Гц.
Гц. Гц,
Гц,
 Гц.
Гц. Гц,
Гц,
 Гц.
Гц. Гц,
Гц,
 Гц.
Гц. Гц,
Гц,
 Гц.
Гц.





 ?
?