Определённый интеграл
Как было сказано выше, процедура вычисления неопределённого интеграла сводится к вычислению первообразной функции и не несёт в себе большой смысловой нагрузки.
Для того, чтобы перейти уже непосредственно к применению системы Mathcad для вычисления определённого интеграла, вспомним теоретический раздел, посвящённый определённому интегралу из курса математики.
Рис.5.18 - Геометрическая трактовка в понятию определённый интеграл.
Р
ассмотрим
на координатной плоскости область D,
ограниченную осью Ox , графиком
непрерывной функции y=
f (x), заданной на отрезке [a;b],
и двумя отрезками вертикальных прямых
x = a и, x
= b , соединяющих точки оси
Ox с точками графика (см.
рис.5.18).
Площадь этой
области называется определенным
интегралом функции
f(x) на отрезке [a;b] и обозначается
символом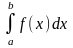 
.
При этом число а называется нижним пределом интегрирования, а число b – верхним.
Далее вспомним формулу Ньютона-Лейбница, которая вносит ясность в вычисление определённого интеграла.
Связь между определенным и неопределенным интегралом устанавливает Формула Ньютона-Лейбница. Если f (x) непрерывна на отрезке [a,b], и F(x) - некоторая первообразная функции f (x), то
.
Разность
в правой части формулы Ньютона-Лейбница
обозначается специальным
символом
(здесь
читается как «подстановка от a
до b», поэтому
формула Ньютона-Лейбница обычно
записывают так:
.
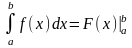Таким образом, задача вычисления определенного интеграла сводится к нахождению первообразной (неопределенного интеграла) и вычислению разности ее значений при верхнем и нижнем пределе интегрирования.
Разберём следующий пример.
Вычислим площадь под синусоидой (вычисление определённого интеграла):
.
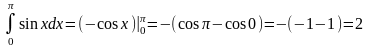Вычислим площадь под параболой (вычисление определённого интеграла):
.
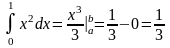Прежде чем перейти к инструменту системы Mathcad для вычисления определённого интеграла, давайте посмотрим, каким образом, основываясь на определении определённого интеграла по Ньютону-Лейбницу, можно вычислить определённый интеграл.
Рис.5.19 - Вычисление определённого интеграла средствами неопределённого интеграла.
Аналогичный пример рассмотрим со степенной функцией.
Рис.5.20 - Вычисление определённого интеграла средствами неопределённого интеграла.
Хочется обратить ваше внимание на подчеркивание функции F(x), как в первом, так и во втором примере. Это подчеркивание связано не с ошибкой, которая возникает в процессе вычисления в системе Mathcad, а с тем, что данная функция была либо определена и использована ранее (имеется в виду её идентификатор, название функции), либо переопределяет какуюто внутреннюю функцию системы, т.е. ведётся её перезапись.
А теперь познакомимся собственно с возможностями системы Mathcad по вычислению определённого интеграла. Для того, чтобы вызвать оператор вычисления определённого интеграла, необходимо на панели Исчисления найти значок Определённый интеграл. После его нажатия на экране системы появится следующий символ.
Рис.5.21 - Значок определённого интеграла.
Его основные отличия от значка неопределённого интеграла заключаются в том, что в нём есть черные квадратики для внесения туда пределов интегрирования. Соответственно верхний значок – это верхний предел интегрирования, нижний значок – это нижний предел интегрирования. Например, выражения, которые были вычислены ранее при помощи неопределённого интеграла, могут быть вычислены при помощи определённого интеграла следующим образом.
Пример вычисления определённого интеграла.
Необходимо обратить внимание на следующую вещь. Для того, чтобы получить результат в неопределённом интеграле, необходимо было использовать оператор Символьное вычисление, который располагается на панели Символьная. Это было сделано для того, чтобы при вычислении неопределённого интеграла результат был выдан в виде функции, т.е. был выдан символьный результат. Однако в случае определённого интеграла мы получаем численное значение. Поэтому для получения результата необходимо использовать оператор Вычислить численно, который располагается на панели Калькулятор. Однако это не исключает возможность использования оператора Символьное вычисление, который располагается на панели Символьная при решении численных задач. Обратим внимание на следующий пример.
Рис.5.22 - Применение символьного оператора для вычисления числовых значений.
Иногда полезно получать результат вычисления именно в таком виде, нежели в числовом. Смотрите пример ниже.
Применение численного оператора.
Далее рассмотрим основные свойства определённого интеграла и докажем их на примере вычислений в системе Mathcad.
Первое свойство. Константу можно выносить за знак определенного интеграла
.
Данное свойство можно пояснить на примере вычисления в системе Mathcad определённого интеграла, например, от степенной функции.
Рис.5.23 - Демонстрация первого свойства определённого интеграла.
Обратите внимание в этом примере, что результат нахождения определённого интеграла можно записать в переменную и в дальнейшем применять её для расчётов.
В
торое
свойство. Интеграл от суммы (разности)
функций равен сумме (разности) интегралов.
Демонстрация второго свойства определённого интеграла.
Е
сли
обращать внимание на синтаксис записи
определённого интеграла в системе
Mathcad, то также справедлива
следующая запись.
Демонстрация второго свойства определённого интеграла.
Третье свойство. Если f(х) интегрируема по отрезку [а, b] и точка c принадлежит этому отрезку, то
.
В
системе Mathcad это может
выглядеть следующим образом.
Демонстрация третьего свойства определённого интеграла.
Помимо демонстрации третьего свойства определённого интеграла, здесь также можно обратить внимание на то, что сами пределы интегрирования могут задаваться непосредственно через переменную, которая была определена выше или значение которой было получено как результат вычисления каких-либо выражений.
Четвертое свойство. Смена знака равносильна смене пределов интегрирования
.
Д
окажем
это при помощи системы Mathcad.
Демонстрация четвёртого свойства определённого интеграла.
После того как были даны основные определения определённого интеграла, а также разобраны примеры о том, как работает с определёнными интегралами система Mathcad, перейдём непосредственно к приложению определённого интеграла.