Лабораторная работа № 5

Цель работы: определение неопределенных и определенных интегралов в программе MathCad с использованием символьных операций.

Указания к выполнению лабораторной работы:

I. Первообразная и неопределённый интеграл

Прежде чем перейти к вычислению неопределённых интегралов в системе Mathcad, необходимо вспомнить основные понятия и определения, касающиеся данного раздела курса математики.

Функция F(x) называется первообразной для функции f (x) на интервале (a,b) (конечном или бесконечном), если в каждой точке этого интервала f (x) является производной для F(x) , т.е.

F'(x) = f (x).

Из этого определения следует, что задача нахождения первообразной обратна задаче дифференцирования. Необходимо по заданной функции f (x) найти функцию F(x) , производная которой равна f (x).

Первообразная определена неоднозначно: например для функции первообразными будут и функция ln x, и функция ln x+1:

(ln x)' =(ln x +1)' = .

Необходимо напомнить, что операция интегрирования обратна операции дифференцирования. При выполнении каких-либо действий с исследованием функций, вычисления производных и прочее, рекомендуется всегда строить её график. Это во многом способствует лучшему пониманию материала, а главное – смысла исследования функции.

Рис. 5.1 - Оператор «Неопределённый интеграл» на панели Матанализ.

Для вычисления неопределённого интеграла на панели Матанализ используется оператор Неопределённый интеграл, значок которого полностью соответствует применяемому значку интеграла в математике. При нажатии на этот значок на рабочем столе системы Mathcad появится шаблон, который необходимо будет заполнить для вычисления неопределённого интеграла функции (см. рис.5.1).

При нажатии на этот значок на рабочем столе системы Mathcad появится шаблон, который необходимо будет заполнить для вычисления неопределённого интеграла функции. В чёрный квадратик, который располагается между знаком интеграла и символом «d» необходимо вписать имя функции вместе с переменной, от которой эта функция зависит. На это место можно вписывать либо непосредственно имя функции или саму функцию. Во второй черный квадратик необходимо вписать переменную, по которой будет происходить интегрирование заданной функции. Для получения результата необходимо воспользоваться командой Символьный знак равенства, который располагается на панели Вычисления.

Для примера вычислим интеграл от тригонометрических функций.

Вычисление неопределённого интеграла от тригонометрических функций.

На следующем примере продемонстрируем одно отличительное свойство вычисления определённого интеграла в системе Mathcad. Из курса математики известно, что

и .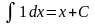

Рис. 5.2 - Вычисление неопределённого интеграла в системе Mathcad от «0» и «1».

Однако при вычислении этих же интегралов в системе Mathcad мы получим (см. рис.5.2).

Как и в этом случае, так и в случае вычисления неопределённого интеграла от и от . Mathcad не выдаёт константу C. Это объясняется тем, что для Mathcad воспринимает её как переменную, поэтому это всегда надо учитывать, когда в дальнейшем будут решаться задачи связанные с дифференциальными уравнениями, где будут существовать начальные условия.

На следующих примерах посмотрим, как при помощи системы Mathcad можно продемонстрировать другие свойства неопределённого интеграла. Для примера возьмём интегрирование показательной и степенной функций.

Из курса математики известно, что

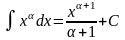и .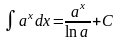

Далее приведём примеры вычисления этих функций в системе Mathcad.

Для степенной функции в общем и частном видах (необходимо также обратить внимание на то, что Mathcad не выдаёт константу интегрирования).

Пример вычисления неопределённого интеграла от степенной функции в общем и частном видах.

Для показательной функции в общем и частном видах.

Пример вычисления неопределённого интеграла от показательной

функции в общем и частном видах.

Рис. 5.3 - вычисления неопределённого интеграла от дробной функции

Приведём пример ещё нескольких наиболее распространённых функций из таблицы неопределённых интегралов, которые наиболее часто встречаются в задачах (см.рис.5.3).

Здесь стоит обратить внимание на то, что константа а, которая располагается в подынтегральной функции, необязательно должна иметь квадратную степень. Например, если стоит константа 4, то её можно представить, как 2². Если же стоит константа 3, то её можно представить как . Аналогично и с другими табличными значениями интегралов. Приведём ещё несколько примеров.

Рис. 5.4 - вычисления неопределённого интеграла

Следует помнить, что Mathcad не всегда корректно может вычислить неопределённый интеграл в общем виде, однако в частном случае вычисление будет произведено верно.

Рис. 5.5 – Некорректное вычисления неопределённого интеграла в общем виде

Фактически операция вычисления неопределенного интеграла является бесполезной, и предназначена только для того, чтобы увидеть, как собственно выглядит первообразная для данной функции. Это объясняется тем, что невозможно вычислить какое-то значение у получившейся функции, не говоря уже о том, что невозможно будет построить график этой функции. Всё это делает операцию символьного дифференцирования, показательной операцией, чтобы просто «воочию увидеть» первообразную от заданной функции.

Такой способ вычисления интеграла, когда из панели Матанализ вызывается оператор Неопределённый интеграл, после чего вписывается подынтегральная функция и при помощи символьного знака равенства выводится результат вычисления, является достаточно редким и при больших расчётах применяется только как проверочный способ. В большинстве случаев необходимо вычислить как неопределённый, так и определённый интеграл от функции, которая была уже задана ранее, причём результат вычисления неопределённого интеграла необходимо также записать в функцию и при дальнейших расчётах найти значение этой функции в какой-либо точке или построить её график.

Ниже приведен пример, который иллюстрирует, каким образом, вычисляется неопределённый интеграл от функции, которая была задана ранее и как результат вычисления записывается в функцию.

Рис. 5.6 - вычисления неопределённого интеграла от функции, заданной заранее

Приведем ещё один пример.

Рис. 5.7 - вычисления неопределённого интеграла

Помимо необходимости вычисления интеграла от функции, которая была задана ранее, а также необходимости записи результата вычисления в функцию, существует также необходимость нахождения значения результирующей функции в какой-либо точке.

Рассмотрим следующий пример.

Рис. 5.8 - вычисления неопределённого интеграла

Обратите внимание на следующее. Для того, чтобы вычислить значение функции в какой-либо точке, необходимо произвести вы-числение в качестве «символьного вычисления». При этом Mathcad может выдавать значения типа ln(2) или e² и прочее, т.е. не выводя само число. Поэтому для того, чтобы получить сам результат, необходимо скопировать выражение символьного результата при помощи оператора Вычислить численно на панели Калькулятор и получить это число, как показано на примере выше.

Помимо того, что данные могут вноситься непосредственно вместо переменной в результирующей функции, также можно за-даваться переменные, которые уже заранее содержат численные значения. Их можно использовать для вычисления значения функции, как подынтегральной, так и функции, которая является результатом интегрирования подынтегральной функции.

На следующем примере разберём этот случай.

Рис. 5.9 - вычисления неопределённого интеграла

На рисунке ниже показано, что Mathcad «отказывается» строить график первообразной функции. Как построить график первообразной функции разберём в разделе «Определённый интеграл».

Рис. 5.9 - Mathcad «отказывается» строить график первообразной функции. Для построения графика см.раздел «Определённый интеграл».

Помимо того, что приходится вычислять неопределённые ин-тегралы от функции одной переменной, в большинстве как математических, так и инженерных задач приходится вычислять как неопределенные, так и определенные интегралы функции нескольких переменных. Приведем несколько примеров на вычисление интегралов от функции нескольких переменных.

Рис. 5.10 - Пример вычисления неопределенного интеграла

от функции двух переменных

Рис. 5.11 - Пример вычисления неопределённого интеграла от функции трёх переменных

Зачастую, помимо того, что есть необходимость вычислять неопределённый интеграл от функции нескольких переменных, также существует необходимость вычислять значения первообразной нескольких переменных в заданной точке.

Приведем ниже пример такого вычисления.

Рис. 5.12 - Пример вычисления неопределённого интеграла от функции нескольких переменных

Мы разобрали возможности системы Mathcad для вычисления неопределенных интегралов. В следующем разделе будут приведены примеры вычисления неопределённых интегралов в системе Mathcad.