2. Расчет комплексных значений тока в заданной ветви схемы в установившемся режиме при действии гармонических источников сигнала методом узловых потенциалов

Составлению требуемых ММЦ должны предшествовать определенные подготовительные этапы.

Для метода узловых потенциалов:

1. эквивалентное преобразование генераторов напряжения в генераторы тока, комплексные значения которых записываются в алгебраической форме;

2. расчет комплексных проводимостей ветвей (часто результат выгоднее оставить в виде простых дробей, а не десятичных);

3. изображение нового варианта модели цепи с учетом предыдущих действий;

4. выбор опорного узла и нумерация всех остальных узлов, указание направления искомого тока ветви и выражение его через соответствующие узловые потенциалы;

5. расчет собственных и взаимных проводимостей узлов (не стремитесь обязательно перейти от простых дробей к десятичным);

6. вычисление суммарных задающих токов в узлах (ток, подтекающий к узлу, берется со знаком «+», оттекающий от узла – со знаком «−»).

1. Эквивалентное преобразование генераторов напряжения в генераторы тока

Преобразование производиться по следующей схеме:

Значения эквивалентных источников тока:

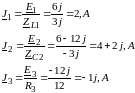
2. Расчет комплексных проводимостей ветвей

3. Изображение нового варианта модели цепи с учетом предыдущих действий

Рисунок 12 – Модель цепи в символической форме для расчета методом узловых потенциалов с буквенными обозначениями

Рисунок 13 – Модель цепи в символической форме для расчета методом узловых потенциалов с числовыми значениями

Сделанный выбор опорного узла обеспечивает ранее принятое направление искомого тока в схеме и требует вычисления единственного узлового потенциала при этом .

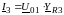Типовая ММЦ по МУП в общем виде:

Собственные проводимости узлов:

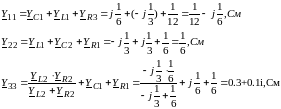
Взаимные проводимости узлов:

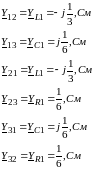
Суммарные задающие токи узлов в амперах:

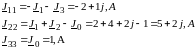
Типовая ММЦ по МУП в цифровом виде:

Запишем систему в матричном виде

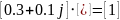
По правилу Крамера

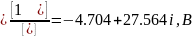
Искомый ток:

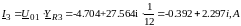
Токи совпали.

7. Мгновенное значение искомого тока

Теперь, когда результаты обоих методов совпали, перейдем к выражению для мгновенных значений искомого тока

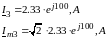
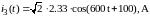
8. Комплексная мощность ветви c током

Вырабатываемая комплексная мощность:

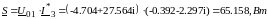
Потребляемая активная мощность:

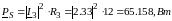
В ветви выделяется активная мощность

9. Вычисление максимальной активной мощности в ветви

Решить задачу подбора сопротивления заданной ветви с целью выделения в ней максимальной активной мощности можно с помощью теоремы об эквивалентном генераторе. Для этого заданная ветвь (та, для которой вычислялся ток) удаляется, а оставшаяся часть схемы заменяется эквивалентным генератором. В этом случае задача сводится к известному соединению генератор – нагрузка.

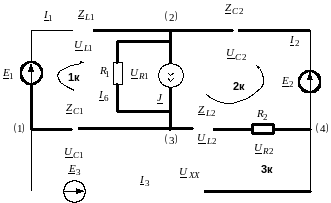
Рисунок 14 – Модель цепи для метода эквивалентного генератора

Определим значение холостого хода:

(3 контур по второму закону Кирхгофа)

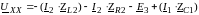
Определяем токи и 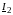методом Кирхгофа:

В результате модель цепи будет имеет =2 узла, =4 ветвей , ;

= – 1 = 1 уравнения по первому закону Кирхгофа;

= – - = 2 уравнения по второму закону Кирхгофа.

Количество уравнений должно быть равно количеству неизвестных токов:

Узел 1:

Для трех элементарных контуров составляем уравнения по второму закону Кирхгофа:

1к:

2k:

Преобразуем уравнения по второму закону Кирхгофа:

1к:

2k:

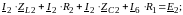
Подставляем числовые значения:

1к:

2k:

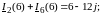
Составляем матричное уравнение:

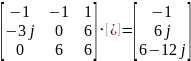
Решаем по методу Крамера:

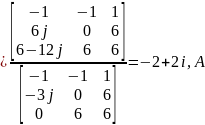
Определим значение холостого хода:

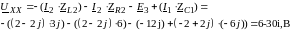
Определим Z_ЭГ как входное сопротивление Z_БВ, для чего изобразим рабочую модель с учетом того, что идеальный источник тока имеет бесконечно большое сопротивление, а идеальный источник напряжения нулевое сопротивление при «обнуленных» источниках.

Рисунок 15 – Рабочая модель

Производим преобразование треугольника в звезду:

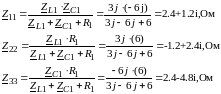
Рисунок 16 – Рабочая модель

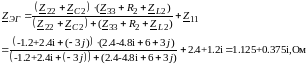
Для получения P_Amax ветвь надо сопротивление нагрузки сделать равным:

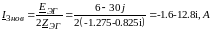
Вычисляем значение тока :

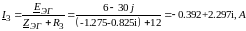
Токи совпали.