3. Уравнения баланса мощности для комплексных значений

Для записи уравнений баланса вырабатываемой и потребляемой комплексной мощности воспользуемся рисунком 3:

Вырабатываемая комплексная мощность:

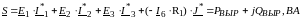
Потребляемая активная мощность:

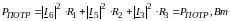
Потребляемая активная мощность:

При правильном расчете токов и напряжений в модели цепи потребляемая и вырабатываемая мощность должны быть равны, т.е. баланс должен сойтись.

4. Расчет все токов и напряжений при действии постоянных источников е и j

Воспользуемся системой уравнений, полученных в пункте 2.3., и вычислим значения токов и напряжений.

Представим систему уравнений в матричном виде:

Подставим в матрицу числовые значения:

Определим значение тока 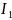методом Крамера:

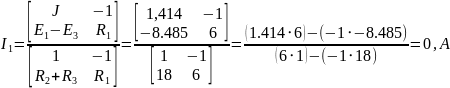
Для нахождения тока воспользуемся уравнением по первому закону Кирхгофа:

Определим значения напряжений при действии постоянных источников сигнала:

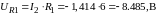
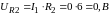
Для определения напряжения на емкостных элементах воспользуемся рисунком 4 и составим уравнения по второму закону Кирхгофа:

1к:

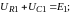
2k:

Для проверки правильности решения составим баланс активной мощности:

Баланс активной мощности сошелся.

5. Вычисление значения входного сопротивления на постоянном токе и при частоте 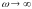относительно источника сигнала 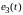полагая, что значения остальных равны нулю.

   1. Вычисление значения входного сопротивления на постоянном токе

Для получения эквивалентной схемы на постоянном токе (ω = 0), учесть, что сопротивление индуктивного элемента обращается в ноль,

а сопротивление емкостного в бесконечность.

Рисунок 6 – Модель цепи для постоянных значений при действии источников постоянных сигналов

Рисунок 7 – Вспомогательная модель цепи для расчета входного сопротивления для постоянного времени

2. Вычисление значения входного сопротивления при частоте

Для получения эквивалентной схемы на постоянном токе ( ), учесть, что сопротивление индуктивного элемента обращается в бесконечность,

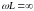
а сопротивление емкостного в ноль.

Рисунок 8 – Модель цепи для расчета входного сопротивления при частоте

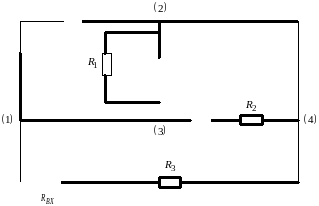
Рисунок 9 – Вспомогательная модель цепи для расчета входного сопротивления при частоте

6. Расчет комплексных значений тока в заданной ветви схемы в установившемся режиме при действии гармонических источников сигнала методами контурных токов и узловых потенциалов.

   1. Расчет комплексных значений тока в заданной ветви схемы в установившемся режиме при действии гармонических источников сигнала методом контурных токов

Составлению требуемых ММЦ должны предшествовать определенные подготовительные этапы.

Для метода к о н т у р н ы х т о к о в:

1. расчет комплексных сопротивлений ZL и ZC;

2. эквивалентное преобразование генераторов тока в генераторы напряжений;

3. запись значений задающих э.д.с. в комплексной алгебраической форме;

4. изображение нового варианта модели цепи с учетом предыдущих

действий;

5. выбор и указание на модели контурных токов и искомого тока, запись искомого тока через соответствующие контурные;

6. расчет собственных и взаимных сопротивлений контуров, а также суммарных э.д.с. каждого контура.

1. Расчет комплексных сопротивлений ZL и ZC

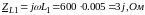
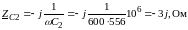
2. Эквивалентное преобразование генераторов тока в генераторы напряжений

Преобразование производиться по следующей схеме:

Значение эквивалентного источника напряжения:

3. Запись значений задающих э.д.с. в комплексной алгебраической форме

Преобразование комплексного числа из показательной формы в алгебраическую производиться следующим образом:

4. Изображение нового варианта модели цепи с учетом предыдущих действий

При расчете схемы методом контурных токов в схему вводится фиктивные токи, которые замыкаются в независимых замкнутых контурах, отличающихся друг от друга наличием хотя бы одной новой ветви.

Определяем число уравнений для контурных токов:

Модель цепи в символической форме для расчета методом контурных токов с буквенными обозначениями, представлена на рисунке 10:

Рисунок 10 – Модель цепи в символической форме для расчета методом контурных токов с буквенными обозначениями

Модель цепи в символической форме для расчета методом контурных токов с численными значениями, представлена на рисунке 11:

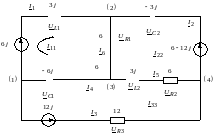
Рисунок 11 – Модель цепи в символической форме для расчета методом контурных токов с численными значениями

Искомый ток

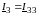
Типовая ММЦ по МКТ в общем виде:

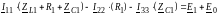
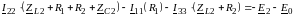
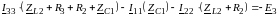
Собственные сопротивления контуров:

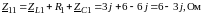
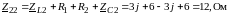
Взаимные сопротивления контуров:

Собственные источники ЭДС:

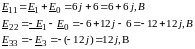
Типовая ММЦ в цифровой форме:

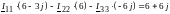
Разделим все уравнения на 3:

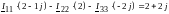
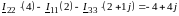
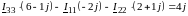
ММЦ в матричной форме:

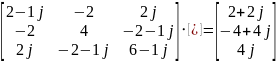
По правилу Крамера искомый ток