21. Основные теоремы о пределах.

Теорема 1. Предел постоянной величины равен самой постоянной:

c = c.

Теорема 2. Предел суммы (разности) двух функций равен сумме (разности) их пределов:

= f(x) φ(x).

Теорема 3.Пределпроизведения двух функций равен произведению их пределов:

= f(x) φ(x).

Теорема 4. Предел дроби равен пределу числителя, деленному на передел знаменателя, если предел знаменателя не равен нулю:

,   0.

Теорема 5. (О пределе промежуточной функции) Если в окрестности точки x₀ выполняются неравенства:

и =   = А, то

22. Вычисление предела. Раскрытие неопределенностей (0/0) и (∞/∞).

При вычислении пределов функций формальная подстановка вместо х предельного значения   часто приводит к неопределенным выражениям вида:   ,   ,   ,   ,  ,   ,   .

Выражения вида   ,   ,   ,   ,   ,   ,   называются неопределенностями.

Вычисление предела функции в этих случаях называют раскрытием неопределенности.

Раскрывать неопределенности позволяет:

• упрощение вида функции (преобразование выражения с использованием формул сокращенного умножения, тригонометрических формул, домножением на сопряженные выражения с последующим сокращением и т.п.);

• использование замечательных пределов;

• применение правила Лопиталя;

• использование замены бесконечно малого выражения ему эквивалентным(использование таблицы эквивалентных бесконечно малых).

Неопределенность вида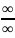 

Если   и   при   (   ), то говорят, что их частное  представляет собой неопределенность вида .

Правило.Чтобы раскрыть неопределенность вида   , заданную отношением двух многочленов, надо и числитель и знаменатель разделить на самую высокую входящую в них степень х.

Неопределенность вида 

Если требуется найти 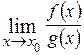  , где   и   − бесконечно малые функции при   (   ), т.е.   , то в этом случае вычисление предела называют раскрытием неопределенности вида   . Правило.Чтобы раскрыть неопределенность вида   , заданную отношением двух многочленов, надо и в числителе и в знаменателе выделить критический множитель и сократить на него дробь.

23. Непрерывность функции в точке и на промежутке. Непрерывность основных элементарных функций.

Непрерывность функции в точке

1)Функция у=f (х) называется непрерывной в точке х_о, если выполнены следующие три условия: 1)функция определена в точке х_о и её окрестности. 2)существует конечный предел функции в точке х_о. 3)этот предел равен значению функции в точке х_о, т.е. lim f(x)= f(x₀)

2) Функция у=f (х) называется непрерывной в точке х_о, если выполнены следующие условия: 1)функция определена в точке х_о и её окрестности. 2)существуют конечные односторонние пределы lim f(x)=f(x₀-0) и lim f(x)=f(x₀+0). 3)эти пределы равны между собой и равны значению функции в точке х₀, т.е. lim f(x)-lim f(x)=f(x₀)

3) Функция у=f (х) называется непрерывной в точке х_о, если выполнены следующие три условия: 1)функция определена в точке х_о и её окрестности.2) бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции: lim y= lim (f(x₀+x)-f(x₀))=0

Свойства:

1. Если функции f(x) и g(x) непрерывны в точке х_о, то функции f(x)+-g(x), c*f(x) (с-постоянная), f(x)*g(x) и f(x)/g(x) (при условии что g(x₀) не = 0) также непрерывна в точке х_о

2. Если функция u=q (x) непрерывна в точке х_о, а функция у=f(u) непрерывна в точке u₀=q(x₀), то сложная функция у=f(q(x)) непрерывна в точке х_о

Непрерывнасть функции на отрезке

Функция у=f(x) наз-ся непрерывной на отрезке [a;b] , если она непрерывна в каждой точке этого отрезка (в точке а непрерывна справа, т.е. lim f(x)=f(a), а в точке b непрерывна слева, т.е. lim f(x)=f(b))

Свойства функций, непрерывных на отрезке:

1.если функция y=f(x) непрерывна на отрезке [a,b], то она ограничена на этом отрезке (первая теорема Вейерштрасса)

2.если функция y=f(x) непрерывна на отрезке [a,b], то на этом отрезке она достигает достигает своего наименьшего значения m и наибольшего значения М (вторая теорема Вейерштрасса)

3.если функция y=f(x) непрерывна на отрезке [a,b] и на его концах принимает значения разных знаков то внутри отрезка существует хотя бы одна точка такая что функция=0 (теорема Больцано-коши).

Теорема (о непрерывности основных элементарных функций).

Основные элементарные функции непрерывны в области определения.

Аналогичная теорема имеет место для элементарных функций, то есть функций, полученных из основных элементарных с помощью операций сложения, вычитания, умножения, деления и суперпозиции (функция от функции).

Теорема (о непрерывности элементарных функций).

Элементарные функции непрерывны в области определения.