
- •1. Вектор. Основные понятия.
- •2. Линейные операции над векторами. Свойства линейных операций.
- •3. Проекция вектора на ось.
- •4. Координаты вектора на плоскости и в пространстве.
- •5. Длина и направление вектора. Разложение вектора по базису.
- •6. Действие над векторами в координатной форме. Условие коллинеарности векторов.
- •7. Скалярное произведение и его свойства.
- •8. Применение скалярного произведения.
- •9. Понятие об уравнении линии на плоскости и в пространстве. Уравнение окружности.
- •10. Уравнение прямой. Различные виды уравнений прямой.
- •11. Нахождение углов между прямыми на плоскости. Условия параллельности и перпендикулярности прямых.
- •12. Уравнение прямой в пространстве: параметрические и канонические.
- •13. Уравнения плоскости.
- •14. Понятие угла между 2 плоскостями и его нахождение. Условия перпендикулярности и параллельности двух плоскостей.
- •15. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости.
- •16. Нахождение точки пересечения прямой и плоскости.
- •18. Понятие сложной функции, обратной функции.
- •19. Понятие предела функций в точке.
- •20. Понятие б.М.В. И б.Б.В. Основные свойства бмв.
- •21. Основные теоремы о пределах.
- •22. Вычисление предела. Раскрытие неопределенностей (0/0) и (∞/∞).
- •23. Непрерывность функции в точке и на промежутке. Непрерывность основных элементарных функций.
- •24. Определение производной.
- •25. Основные правила дифференцирования. Таблица производных.
- •26. Производная от сложных функций.
- •27. Производные более высокого порядка.
- •28. Дифференциал функции.
- •29. Монотонность функции. Достаточное условие монотонности функции на интервале.
- •30. Точки экстремума. Необходимое и достаточное условия существования экстремума. Исследование функции на экстремум.
- •31. Интервалы выпуклости, вогнутости графика функции, точки перегиба.
- •32. Необходимое и достаточное условия существования перегиба графика. Схема исследований функций на перегиб.
- •33. Полное исследование функции и построение графика.
7. Скалярное произведение и его свойства.
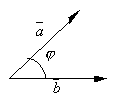
Пусть
даны два вектора
и
,
угол между, которыми равен ![]() .
.
Скалярным произведением
векторов
и
называется
число, равное произведению длин этих
векторов на косинус угла между ними.
Скалярное произведение обозначается ![]() .
Итак,
.
Итак, ![]() .
.
Если один из векторов нулевой, то угол не определен, и скалярное произведение по определения считается равным нулю.
Рассмотрим свойства скалярного произведения.
Скалярное произведение двух векторов подчиняется коммутативному закону, т.е. для любых векторов и
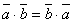 .
.
2.
Для любого числа λ и любых векторов ![]() имеем:
имеем:
![]() .
.
3.
Для любых векторов ![]() выполняется
равенство
выполняется
равенство ![]() .
.
4.
Для любого вектора
выполняется
соотношение![]() .
.
5. Скалярное произведение двух векторов равно нулю тогда и только тогда,когда равен нулю один из сомножителей или векторы перпендикулярны.
Это свойство очевидно из определения скалярного произведения.
Таким образом, необходимым и достаточным условием ортогональности двух векторов является равенство нулю их скалярного произведения.
8. Применение скалярного произведения.
Скалярное произведение векторов применяется для нахождения длины вектора, косинуса угла между векторами, проекции одного вектора на направление другого и установления перпендикулярности векторов.
1) ![]() или
или ![]() .
.
2) 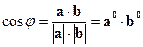 .
.
3) 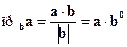 .
.
4) ![]() .
.
9. Понятие об уравнении линии на плоскости и в пространстве. Уравнение окружности.
Уравнением линии на плоскости в декартовой системе координат называют уравнение: F(х;у)=0, которому удовлетворяют координаты (х;у) любой точки этой линии и не удовлетворяют координаты ни одной точки, которые не принадлежат ей.
Линия в пространстве задаётся в общем случае как линия пересечения некоторых поверхностей S1 и S2 .
Система уравнений:
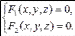
называется уравнением линии в пространстве.
Окружностью называется
линия, каждая точка М(х;у) на которой
находится на одинаковом расстоянии ![]() от
заданной точки
от
заданной точки ![]() ,
называемойцентром
окружности.
Величина
называется радиусом
окружности.
,
называемойцентром
окружности.
Величина
называется радиусом
окружности.
В прямоугольной системе координат уравнение окружности имеет вид
![]() ,
,
где (a;
b) —
координаты её центра, ![]() —
радиус окружности.
—
радиус окружности.
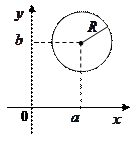
В частности, если центр окружности совпадает с началом координат, т.е. a=0 , b=0 , то уравнение окружности примет вид:
![]()
10. Уравнение прямой. Различные виды уравнений прямой.
Общее уравнение прямой:
1.
![]() ,
(2)
,
(2)
где ![]() —
постоянные коэффициенты,
причём
—
постоянные коэффициенты,
причём ![]() и
и ![]() одновременно
не обращаются в нуль
одновременно
не обращаются в нуль ![]() .
.
Частные случаи этого уравнения:
![]()
![]() —
прямая
проходит через начало координат;
—
прямая
проходит через начало координат;
![]()
![]() —
прямая
параллельна оси
—
прямая
параллельна оси ![]() ;
;
![]()
![]() —
прямая
параллельна оси
—
прямая
параллельна оси ![]() ;
;
![]()
![]() —
прямая
совпадает с осью
;
—
прямая
совпадает с осью
;
![]()
![]() —
прямая
совпадает с осью
.
—
прямая
совпадает с осью
.
