
- •1. Вектор. Основные понятия.
- •2. Линейные операции над векторами. Свойства линейных операций.
- •3. Проекция вектора на ось.
- •4. Координаты вектора на плоскости и в пространстве.
- •5. Длина и направление вектора. Разложение вектора по базису.
- •6. Действие над векторами в координатной форме. Условие коллинеарности векторов.
- •7. Скалярное произведение и его свойства.
- •8. Применение скалярного произведения.
- •9. Понятие об уравнении линии на плоскости и в пространстве. Уравнение окружности.
- •10. Уравнение прямой. Различные виды уравнений прямой.
- •11. Нахождение углов между прямыми на плоскости. Условия параллельности и перпендикулярности прямых.
- •12. Уравнение прямой в пространстве: параметрические и канонические.
- •13. Уравнения плоскости.
- •14. Понятие угла между 2 плоскостями и его нахождение. Условия перпендикулярности и параллельности двух плоскостей.
- •15. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости.
- •16. Нахождение точки пересечения прямой и плоскости.
- •18. Понятие сложной функции, обратной функции.
- •19. Понятие предела функций в точке.
- •20. Понятие б.М.В. И б.Б.В. Основные свойства бмв.
- •21. Основные теоремы о пределах.
- •22. Вычисление предела. Раскрытие неопределенностей (0/0) и (∞/∞).
- •23. Непрерывность функции в точке и на промежутке. Непрерывность основных элементарных функций.
- •24. Определение производной.
- •25. Основные правила дифференцирования. Таблица производных.
- •26. Производная от сложных функций.
- •27. Производные более высокого порядка.
- •28. Дифференциал функции.
- •29. Монотонность функции. Достаточное условие монотонности функции на интервале.
- •30. Точки экстремума. Необходимое и достаточное условия существования экстремума. Исследование функции на экстремум.
- •31. Интервалы выпуклости, вогнутости графика функции, точки перегиба.
- •32. Необходимое и достаточное условия существования перегиба графика. Схема исследований функций на перегиб.
- •33. Полное исследование функции и построение графика.
1. Вектор. Основные понятия.
Вектор
– направленный
прямолинейный отрезок, т. е. отрезок,
имеющий длину и определенное направление.
Если ![]() –
начало вектора,
–
начало вектора, ![]() –
его конец, то такой вектор обозначается
как
–
его конец, то такой вектор обозначается
как ![]() ,
или
,
или ![]() .
Вектор
.
Вектор ![]() с
началом в точке и концом в точке
называетсяпротивоположным вектору
и обозначается как
с
началом в точке и концом в точке
называетсяпротивоположным вектору
и обозначается как ![]() ,
или
,
или ![]() .
.
Длиной
или модулем вектора называется
длина отрезка ![]() и
обозначается
и
обозначается ![]() .
.
Вектор,
длина которого равна нулю, называется нулевым
вектором и
обозначается как ![]() .
Считается, что он не имеет направления.
.
Считается, что он не имеет направления.
Вектор,
длина которого равна 1, называется единичным
вектором и
обозначается как ![]() .
.
Векторы
и ![]() называются коллинеарными,
если они лежат на одной прямой или на
параллельных прямых. Это обозначается
как
называются коллинеарными,
если они лежат на одной прямой или на
параллельных прямых. Это обозначается
как ![]() .
.
2. Линейные операции над векторами. Свойства линейных операций.
К линейным относятся операции сложения векторов и умножение вектора на число.
Суммой
векторов ![]() и
и ![]() называется
вектор, полученный по правилу сложения
векторов:
называется
вектор, полученный по правилу сложения
векторов:
А) если совместить начала векторов, то суммой будет вектор, начало которого совпадает с началами векторов, а конечная точка- противоположная вершина параллелограмма, сторонами которого будут и ;
В) если совместить начало второго вектора и конечную точку первого, то сумма – вектор, начало которого совпадает с начальной точкой первого вектора, а конечная – с конечной точкой второго.
Суммой конечного числа векторов служит замыкающий вектор:
Вектор ![]() называется противоположным вектору
,
если их длины совпадают, а направления
противоположны.
называется противоположным вектору
,
если их длины совпадают, а направления
противоположны.
Разностью векторов
и
называется
вектор ![]() ,
который является суммой векторов
и
-
.
Вектор
направлен
к концу вектора
,
если
и
приведены
к одному началу.
,
который является суммой векторов
и
-
.
Вектор
направлен
к концу вектора
,
если
и
приведены
к одному началу.
Произведением
вектора
на
число ![]() называется
вектор
называется
вектор ![]() ,
для которого:
,
для которого:
1)
длина в
раз
больше : ![]()
2)
направления совпадают, если ![]() и
противоположны, если
и
противоположны, если ![]()
Для
любого ненулевого вектора ![]() можно
определить орт
вектора:
можно
определить орт
вектора:
Введенные операции называются линейными и обладают рядом свойств:
1)
Сложение векторов коммутативно: ![]()
2)
Сложение векторов ассоциативно: ![]()
3) ![]()
4) ![]()
5)
Умножение вектора на число ассоциативно: ![]()
3. Проекция вектора на ось.
Числовой осью называют прямую, на которой определено:
направление ( → );
начало отсчета (точка О);
отрезок, который принимают за единицу масштаба
.
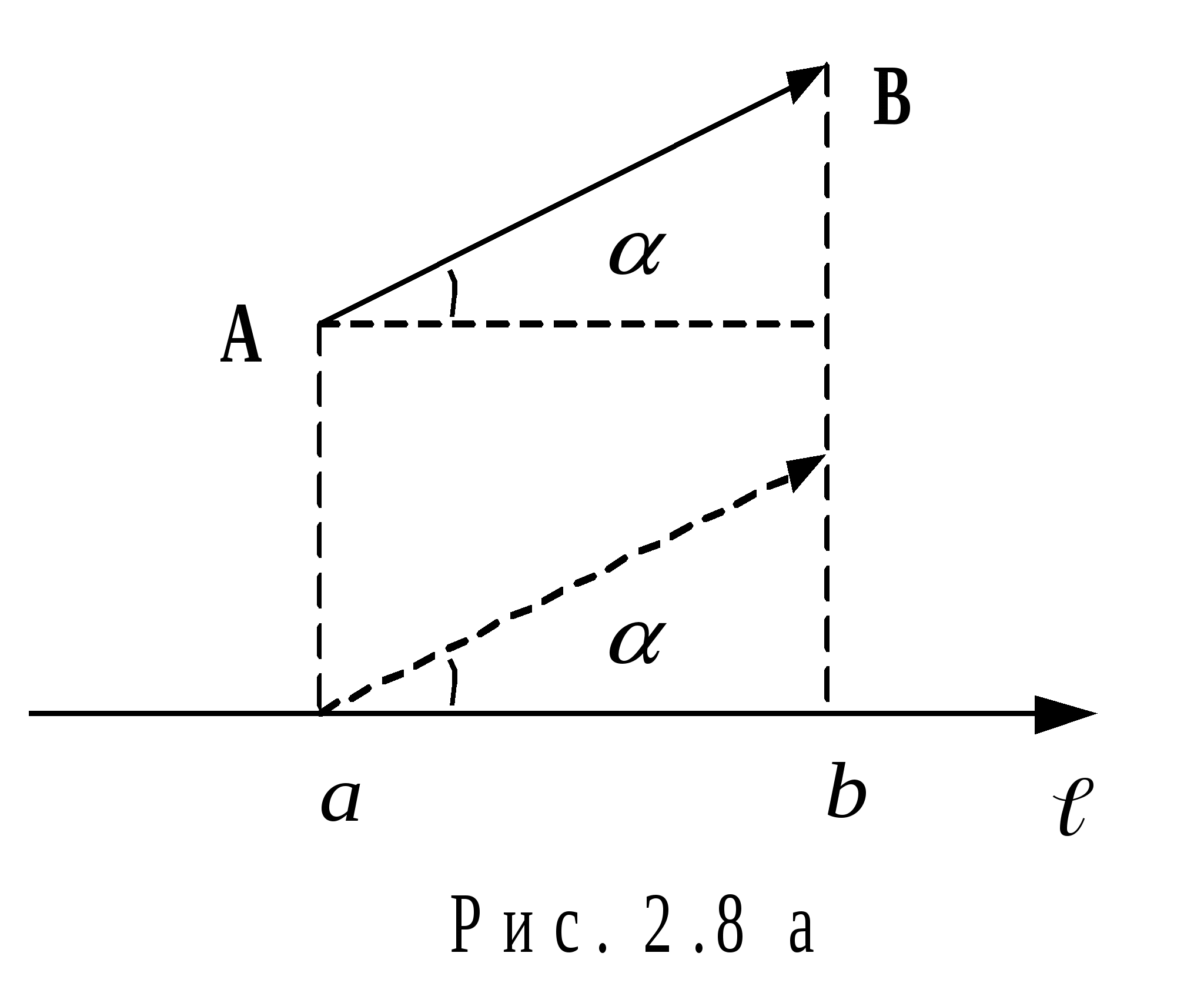
Проекцией
вектора на ось называется
длина отрезка ![]() этой
оси, который расположен между основаниями
проекций начала и конца вектора на ось
. Она берется со знаком плюс, если
направление отрезка совпадает с
направлением оси проекций, и со знаком
минус, если эти направления противоположны.
Обозначение:
этой
оси, который расположен между основаниями
проекций начала и конца вектора на ось
. Она берется со знаком плюс, если
направление отрезка совпадает с
направлением оси проекций, и со знаком
минус, если эти направления противоположны.
Обозначение:![]() .
.
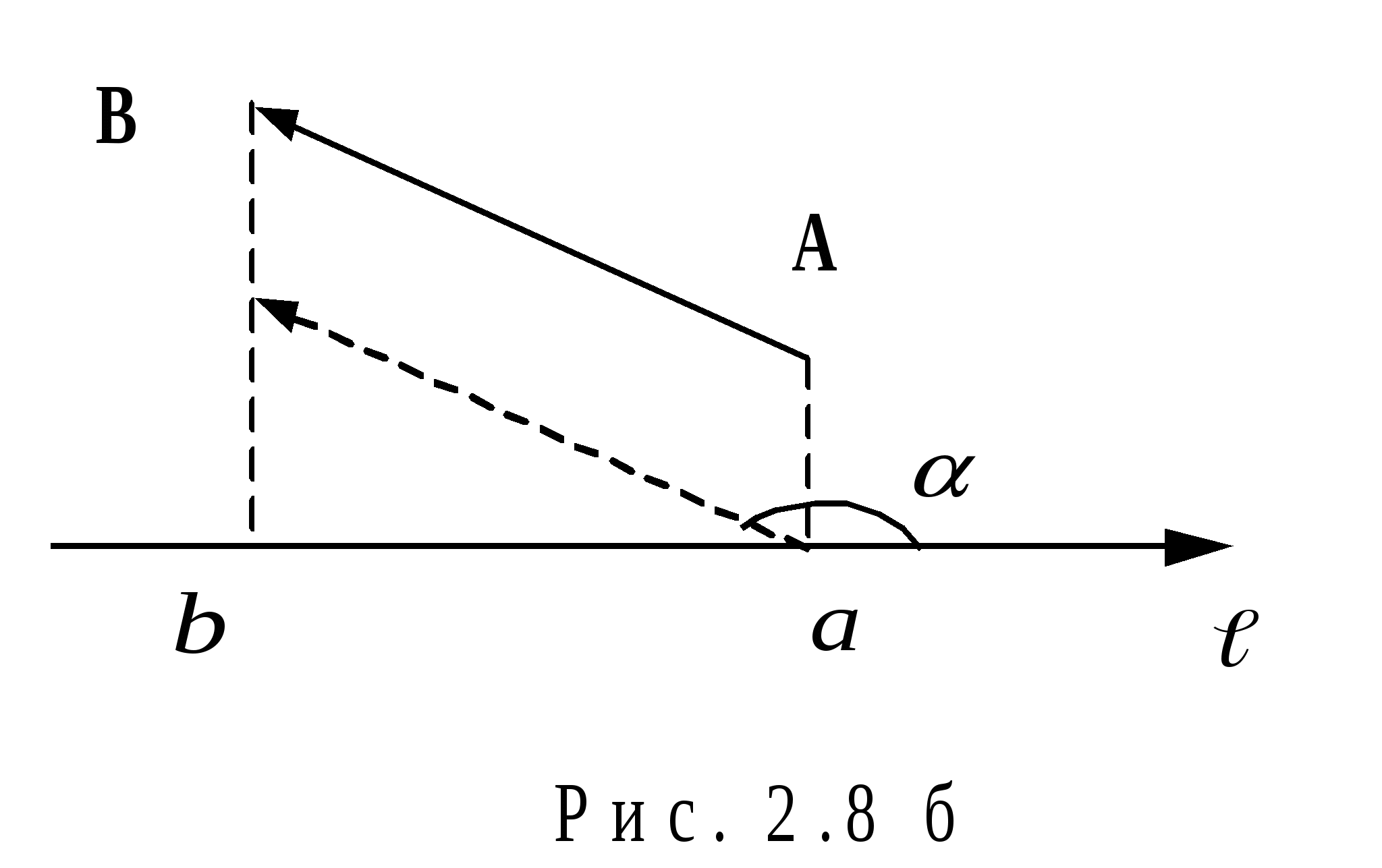
Углом
между вектором и осью называется угол ![]() ,
на который необходимо кратчайшим образом
повернуть ось , чтобы она совпадала с
направлением вектора .
,
на который необходимо кратчайшим образом
повернуть ось , чтобы она совпадала с
направлением вектора .
Свойства проекций:
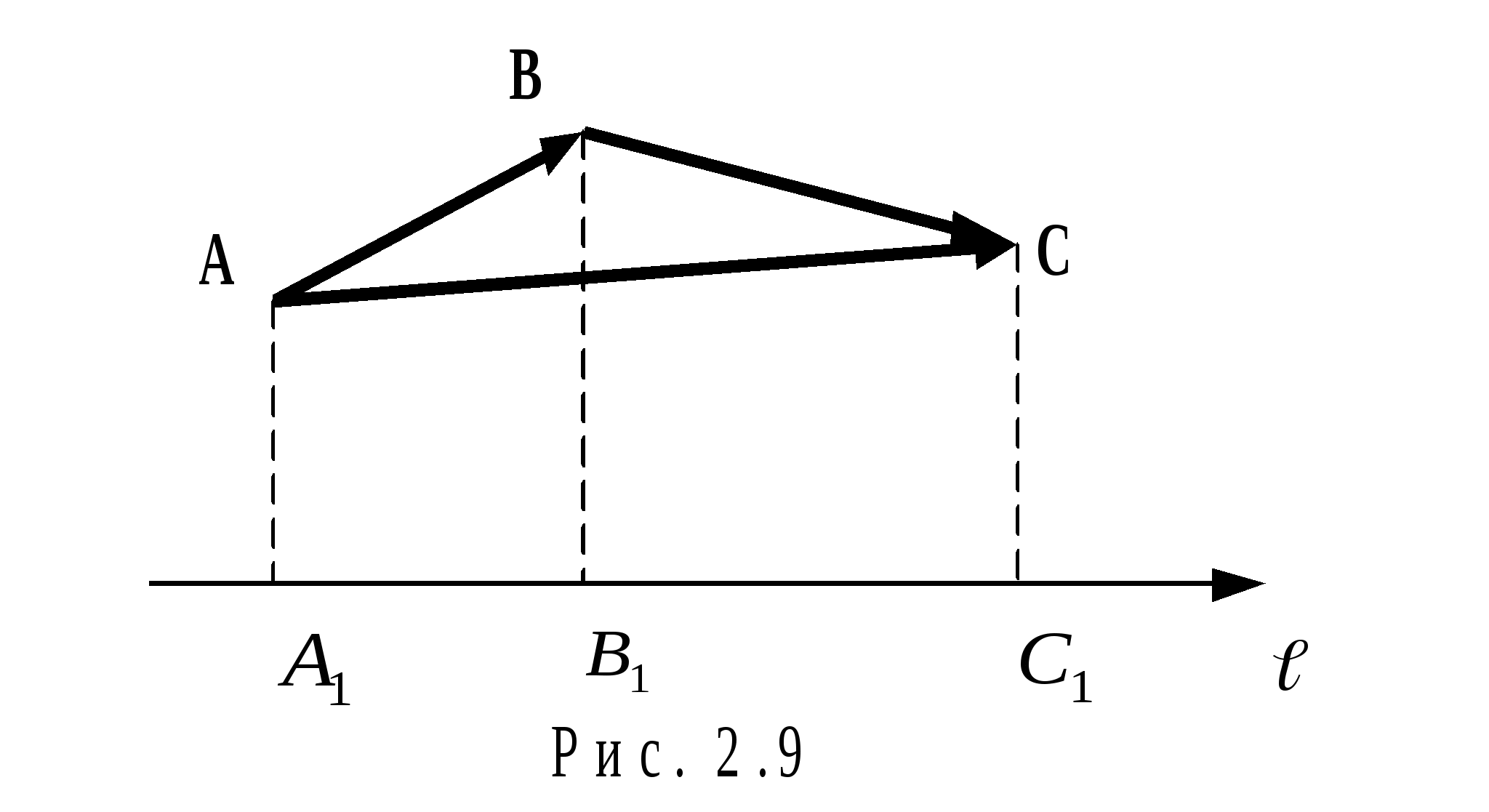
равные векторы имеют равные проекции;
при умножении вектора на число
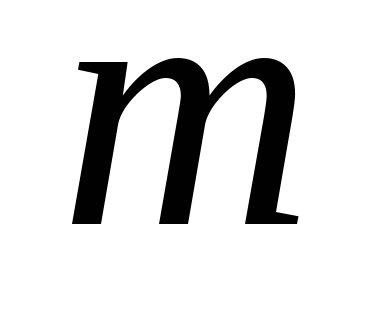 его
проекция на ось также умножается на то
же число;
его
проекция на ось также умножается на то
же число;
- проекция суммы двух векторов на ось равна сумме проекций этих векторов.
