Выверки секстана, три регулировки секстана с целью уменьшения ошибок наблюдений:

1.Параллельность оси трубы секстана плоскости лимба;

Точная выверка производится при стоянке судна в порту или на рейде с помощью диоптров по наблюдениям удаленного не менее чем на 150 метров объекта. Секстан с отфокусированной дневной трубой устанавливается на ящик секстана. Алидаду рас-полагают в середине лимба. Затем на края лимба ставят два диоптра так, чтобы сое-диняющая их линия была примерно параллельна оптической оси трубы. Затем глаз переводят к трубе и поворачивают в небольших пределах секстан так, чтобы в окуляре трубы появилось место, которое наблюдали в створе верхних срезов диоптр. Если горизонтальная линия видна не на середине поля зрения трубы, то, действуя на кольцо стойки трубы верхним и нижним винтами, приводят линию на середину.

2. Перпендикулярность большого зеркала плоскости лимба, выверка выполняется в помещении. Секстан без трубы установить горизонтально на ящик секстана. Алидаду поставить на отсчет около 40° и откинуть светофильтры большого зеркала. Повернуть секстан большим зеркалом к себе, на лимб поставить диоптры около отсчетов 0° и 130° и смотреть мимо внутреннего края большого зеркала на диоптр Д₁ так, чтобы видеть половину диоптра, причем верхняя кромка диоптра должна быть по высоте на середине зеркала. Далее следует освободить алидаду от сцепления с нарезной рейкой и установить ее таким образом, чтобы в большом зеркале наблюдалась половина диоптра Д₂. Расхождение верхних срезов диоптр означает, что большое зеркало не перпендикулярно плоскости лимба. Регулировочным ключом регулировочный винт, добиваются совпадения верхних срезов диоптров Д₁ и Д₂ .

Положение диоптров: до выверки после выверки

3. Перпедикулярность малого зеркала плоскости лимба, эта выверка выполняется на секстане с дневной трубой ночью (по неяркой звезде, находящейся на небольшой высоте, а днем по Солнцу) и алидадой, установленной на отсчет около нуля. Эту операцию производят после установки большого зеркала.

Поворачивая ключом боковой регулировочный винт малого зеркала, смещают дважды отраженное изображение вправо или влево до совпадения по вертикали с прямовидимым. При этом дважды отраженное изображение может переместиться выше или ниже прямовидное, т.е. изменится поправка индекса, которую надо определить заново.

1. Поправка индекса по горизонту. Наводят секстан на горизонт. Дважды отраженное и прямовидное изображение горизонта, линия которого представляется ломаной. Вращая отсчетный барабан секстана, cовмещают дважды отраженное и прямовидное изображение горизонта.

Снимают отсчет индекса О_i по лимбу и определяют поправку индекса по формуле

i = 0°(360°) – О_i .

В данном примере О_i = 359'.1, тогда i = +0'.9

2. Поправка индекса по звезде.

Данный способ аналогичен предыдущему. Необходимо выбрать не слишком яркую звезду на небольшой высоте, навести на неё трубу секстана, и, вращая отсчетный барабан, совместить дважды отраженное изображение звезды с прямовидимым. Снять отсчет индекса О_i и определить поправку индекса.

3. Поправка индекса по Солнцу.

_{Перед зеркалами набрасывают светофильтры разного цвета. Наводят трубу на Солнце и вращением отсчетного барабана приводят дважды отраженное изображение с прямовидимым сначала одним краем, затем другим. При каждом совмещении производится отсчет Оi1} и О _i2.

Поправка индекса по Солнцу определяется из формулы: i = 360° – (О_i1 + О_i2)/2

Достоинством определения поправки индекса по Солнцу является контроль наблюдений. Разность большего и меньшего отсчетов О_i1 – О_i2=4R есть учетверенный измеренный радиус Солнца, который необходимо сравнить с учетверенным радиусом Солнца, выбранным из МАЕ на данную дату. Если разница не превышает по модулю 0,4', то наблюдения качественные и поправка надежная, в противном случае наблюдения следует повторить. Вычисления по этой формуле несколько громоздки. Пример более простого вычисления поправки индекса:

дано О_i1 = 0°29.8', О_i2 =359°26.4'. Вычитаем из 30.0' последовательно минутные разряды О_i1 и О_i2. Итак: а) 30.0' – 29.8' = +0.2', б) 30.0' – 26.4' = +3.6'. i = (+0.2' + 3.6') /2 = +1.9'.

Высота светила, координата горизонтной системы – дуга h вертикала от истинного горизонта до светила в интервале от –90° до 90°. Светило, находящееся под горизонтом, имеет отрицательную высоту, называемую снижением

.

высота видимая, измеренная высота, исправленная поправкой за наклонение видимого горизонта.

h_в = h_изм + (– d)

Все остальные поправки получают по аргументу «видимая высота».

высота глаза наблюдателя е, расстояние по вертикали от глаза наблюдателядо уровня моря. е = ?

высота измеренная, отсчет секстана, исправленный поправкой индекса и инстру-ментальной поправкой s, зависящей от отсчета секстана; s выбирается из таблицы на внутренней стороне крышки ящика секстана

h_изм = ОС + i + s

высота, измеренная над береговой чертой, высота светила, измеренная над предметом, расположенным ближе видимого горизонта: над ватерлинией соседнего судна, во льдах и т.д.

высота, измеренная «через зенит», высота Солнца, измеренная в обратном азимуте, с целью исключения систематических ошибок, помимо этого, горизонт в противоазимуте Солнца четче и точность измерения высоты выше.

высота истинная, дуга вертикала от истинного горизонта до места светила.

высота меридиональная, высота светила в кульминации: H = 90°–± Знак +, если и одноименны и знак –, если разноименны. Эта высота имеет наименование точки N или S полуденной линии, над которой она измерена.

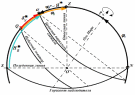
На рисунке меридиональная высота H_s = SQ + Q_N= 90°.

H_s – меридиональное зенитное расстояние.

высота наибольшая, наибольшее значение высоты в серии измеренных высот. Эта высота не совпадает с меридиональной из-за движения судна и изменения склонения Солнца.

высота обсервованная, отсчет секстана ОС, исправленный всеми необходимыми поправками.

высота повышенного полюса, параметр, равный широте места наблюдателя:

h = 

высота соответствуюшая, высота, измеренная симметрично относительно меридиана наибольшей высоты в азимутах 25° – 30°.

высота счислимая, высота h_с, получаемая решением параллактического треугольника.

высота топоцентрическая, угол между истинным горизонтом и истинным положением центра светила в топоцентрической системе координат.

Высотная линия положения (ВЛП), прямая (касательная или хорда), заменяющая круг равных высот около счислимого места.

Уравнение ВЛП:

·cosA_с + ·cos· sinA_с= h_о – h_с.

Г

Галактика, гравитационно-связанная система из звёзд, звёздных скоплений, межзвёзд-ного газа, пыли, и тёмной материи. Все объекты в составе галактики участвуют в движе-нии относительно общего центра масс. Галактики отличаются большим разнообразием: среди них можно выделить сфероподобные, эллиптические галактики, дисковые, спи-ральные галактики, галактики с перемычкой (баром), линзовидные, карликовые, неправильые и т. д. Диаметр галактик от 16 до 800 тысяч световых лет. Для сравнения, диаметр Нашей галактики около 30 100 тысяч световых лет. Разглядеть на небе невоору-жённым глазом можно всего лишь три галактики: туманность Андромеды (видна в северном полушарии), Большое и Малое Магеллановы Облака (видны в южном полушарии).

Туманность Андромеды Скопление Галактик

Солнечная система, все видимые звёзды (их около 300 млрд.), звездные скопления, газовые облака и космическая пыль входят в Нашу Галактику. Она относится к спираль-ным галактикам с перемычкой. В центре Галактики, по всей видимости, располагается сверхмассивная чёрная дыра.

Гелиоцентрическая система мира, представление о том, что Солнце является централь-ным небесным телом, вокруг которого обращается Земля и другие планеты. Провозвест-ником гелиоцентризма можно считать древнегреческого философа Аристарха Самосского (320 - 250 гг. до н.э.). После II века н. э. в эллинистическом мире прочно утвердился геоцентризм, основанный на философии Аристотеля и планетной теории Птолемея – представление об устройстве мироздания, согласно которому центральное положение во Вселенной занимает неподвижная Земля, вокруг которой вращаются Солнце, Луна, планеты и звёзды, а петлеобразное движение планет объяснялось с помощью комбинации деферентов и эпициклов. Обоснование гелиоцентрической системы мира было дано толь-ко через восемнадцать с половиной веков в сочинении Николая Коперника в его труде "Об обращении небесных сфер", изданном в Нюрнберге в 1543 году, где он и привел свой знаменитый рисунок с указанием расположения небесных сфер. В системе Коперника Солнце (1) находится в центре Солнечной системы, вокруг него обращаются Меркурий (2), Венера (3), Земля (4), Марс (5), Юпитер (6), Сатурн (7).

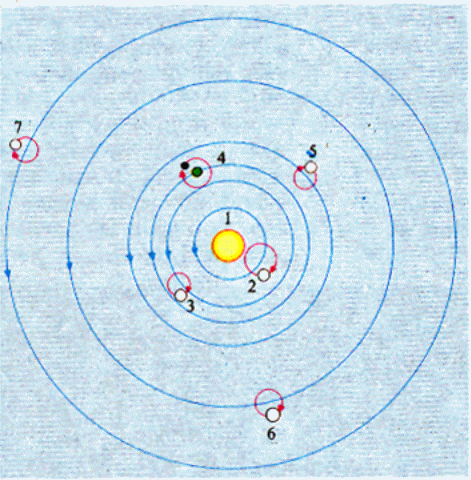
Н.Коперник Гелиоцентрическая система мира

Географическая система координат, роль осей координат выполняют земной экватор и нулевой (гринвичский) меридиан. Координатами, определяющими положение точки на земной поверхности относительно экватора и нулевого меридиана, являются:

Географическая долгота, дуга экватораот начального (нулевого) меридиана до мери-диана места в пределах от 0° до180°, имеющая наименование E или W.

Географическая широта,

1. Угол  между отвесной линией в данной точке и плоскостью экватора.

2. Угол  между осью вращения Земли и плоскостью истинного горизонта.

3. Дуга  меридиана от экватора до данного места.

4. Высота h_PN повышенного полюса.

Широта  меняется в интервале от 0° до 90° и имеет наименование N или S.

Географический меридиан, половина большого круга, проходящего через Северный и Южный географические полюса (через ось вращения Земли) и выбранную точку земной поверхности. Все точки земной поверхности, лежащие на одном меридиане имеют одина-ковую географическую долготу. Вдоль меридианов отсчитывается географическая широта.

Географическая параллель, малый круг на земной поверхности параллельный плоскости земного экватора. Параллель может быть проведена через любую точку земной поверхности. Все точки одной параллели имеют одинаковую географическую широту.

Географические часовые пояса, территории на поверхности Земли, ограниченные меридианами с разностью долгот 15° (± 7,5° относительно среднего меридиана). Средним меридианом нулевого часового пояса считается гринвичский меридиан. Насчитывается 12 восточных и 12 западных часовых поясов. Средний меридиан 12-го часового пояса является линией смены дат.

Географический полюс, точка пересечения оси вращения Земли с земной поверхностью. Различают Северный и Южный полюса. В географических полюсах сходятся все земные меридианы. На них нет сторон света, нет деления на дни и ночи. Широты полюсов = 90°N или = 90°S, полюса не имеют долгот. Географические полюса не занимают неизменного положения, а перемещаются по сложной кривой, не выходя при этом за квадрат со стороной 26 метров. Движение полюсов Земли связано с изменением положения мгновенной оси ее вращения, которое обуславливается сезонными перемещениями атмос-ферных масс, воды в океанах, влиянием упругих и вязких свойств литосферы и др.

Геометрический горизонт, малый круг на поверхности моря, описанный лучом от глаза наблюдателя до наиболее удаленных точек на его поверхности при условии полного отсутствия атмосферы.

Геоид, уровенная поверхность, приблизительно совпадающая со средним уровнем вод мирового океана в невозмущенном состоянии и условно продолженная под материками. Отличие реального среднего уровня моря от геоида может достигать 1м, поверхность геоида везде перпендикулярна отвесной линии.

Главные точки горизонта, точки N и S (точки севера и юга), точки пересечения меридиана наблюдателя с истинным горизонтом и точки W и E (точки запада и востока) – точки пересечения небесного экватора с истинным горизонтом. Точка востока находится справа от направления на север, если встать лицом к N.

_{Глобус «Земное яблоко»}

Глобус, вращающаяся шарообразная модель Земли, другой планеты или небесной сферы с нанесенными на ее поверхность картографическим изображением и координатной системой. Глобус имеет масштаб, систему меридианов и параллелей, условные обозна-чения. Глобус не содержит искажений, присущих картографическим проекциям. По гло-бусу можно производить измерения, не вводя поправок, кроме пересчета расстояний по масштабу. На рисунке – старейший сохранившийся до наших дней. глобус «Земное яблоко», созданный Мартином Бехаймом в Нюрнберге в 1492 году.

Гномон, старинный астрономический инструмент: вертикальный предмет, позволяющий по тени в полдень определять угловую высоту Солнца. Кратчайшая тень указывает и направление истинного меридиана.

Год, условная единица измерения времени, которая исторически означала однократный цикл сезонов (весна, лето, осень, зима). В большинстве стран календарная продолжи-тельность года равна 365 или 366 дням. В настоящее время год употребляется также в качестве временной характеристики обращения планет вокруг звёзд в планетарных системах, в частности Земли вокруг Солнца.

Год звездный, время, за которое Солнце совершает полный оборот относительно направления на выбранную неподвижную звезду – сидерический год. Т_зв = 365.256360 сут.

Год календарный, время обращения Земли вокруг Солнца зп целое число суток: за 365 суток – простой год, за 366 суток – високосный.

Год световой, расстояние, проходимое лучом света за один календарный год.1св.год = 9.5·10¹² км.

Год тропический, время между двумя последовательными прохождениями центром Солнца точки Овна. Продолжительность тропического года 365.242196 средних солнечных суток.

Годовое движение Солнц, движение Солнца по большому кругу небесной сферы, называемому эклиптикой, с запада на восток (в сторону, противоположную вращению небесной сферы). Угол между эклиптикой и небесным экватором 23.5°. Следствием годового движения являются: изменение азимутов точек восхода и захода, изменение меридиональной высоты Солнца и продолжительности дня.

Горизонт, воображаемая линия по которой небо пересекается с поверхностью Земли.

Горизонт геометрический, малый круг на поверхности моря, образованный касательной, проведенной от глаза наблюдателя к поверхности моря (без учета рефракции), максимально удаленный от наблюдателя с высотой глаза е.

Горизонт видимый,

1. Геометрический горизонт, исправленный поправкой за рефракцию. Представляет собой малый круг на поверхности моря, описанный лучом от глаза наблюдателя до наиболее удаленных точек на его поверхности. Зависит от высоты глаза наблюдателя над уровнем моря и величины рефракции. Из-за влияния рефракции видимый горизонт располагается дальше геометрического.

2. Видимая граница (линия кажущегося соприкосновения) неба и земной или водной поверхности, а также небесное пространство над этой границей (говорят: корабль скрылся за горизонтом, Солнце на горизонте и т.д.).

Горизонт истинный, пересечение плоскости истинного горизонта с небесной сферой.

Горизонт искусственный, плоская, горизонтально расположенная зеркальная поверх-ность, используемая при астрономических наблюдениях; обычно – чаша с ртутью, реже – хорошо отполированное плоское стекло. Световые лучи падают на отражающую поверх-ность и попадают в трубу секстана. Измеренный угол, исправленный поправкой индекса, равен удвоенной высоте светила.

Горизонтальный экваториальный параллакс p₀, наибольшая величина суточного параллакса планеты, для наблюдателя на экваторе, когда планета, а конкретнее – Венера или Марс, находится на горизонте. Этот параметр p0 используется при исправлении высот светил и выбирается из последней строки левого разворота ежедневных таблиц, а также может быть получен из соотношения

h = p₀ ·cos OC .

Для Сатурна и Юпитера всегда p₀ = 0. Эту же поправку можно получить из таблицы МАЕ, приведенной на стр. 287.

Град, единица измерения углов, равная 1/100 части прямого угла. В полной окружности 400 град. Град обозначается буквой g. g = 0,9° = 1/400 оборота, /200 рад.

Градиент, вектор, своим направлением указывающий направление наискорейшего воз-растания некоторой величины, значение которой меняется от одной точки пространства к другой, а по величине (модулю), равный быстроте роста этой величины в этом направ-лении. С математической точки зрения градиент – это производная скалярной функции, определенной на векторном пространстве.

Градиент высоты, вектор, направленный по линии азимута в сторону увеличения высоты светила, модуль его равен 1. Градиент высоты равен 1, поэтому при изменении переноса n на 1' ВЛП смещается по Аc на одну милю.

Градус, единица измерения углов, равная 1/90 части прямого угла или 1/360 часть окружности.

Градусная мера дуг и углов, исторически сложившаяся система измерения и сравнения углов. Углы измеряют в градусах (1/360 окружности, обозначается символом °), в угловых минутах (1/60 градуса, обозначается символом '), в угловых секундах (1/60 угловой минуты, обозначается символом "). Соотношение между градусной мерой и часовой:

360° = 24ч, 15° = 1ч, 1° = 4м, 1' = 4с.

Градшток, или посох Якова, или арбалет, инструмент для измерения высоты небесного светила.

Градшток снабжался тремя – четырьмя марто для измерения высот в интервале от 20°до 80°. Этот инструмент в разных вариантах применялся в ХV – XII века.

Гражданские сумерки, сумеречное освещение при снижении Солнца в интервале от захода Солнца т.е. от – 0° до – 6°, это период, в течение которого при хороших атмос-ферных условиях освещения чётко видны наземные объекты; утром в начале или вечером в конце гражданских сумерек чётко различима линия горизонта и при хороших атмос-ферных условиях хорошо видны самые яркие звёзды.

Границы часовых поясов, линии, разделяющие зоны с различным официальными временами. Они не строго следуют вдоль меридианов, а иногда совпадают с админи-стративными границами, руслами рек и пр.

Графический метод весов, способ сложения весов вершин фигуры погрешностей обра-тно пропорционально их весам, он эквивалентен отысканию центра тяжести фигуры.

Графический метод определения места судна на звездном глобусе: измеряются высоты двух светил с фиксацией момента Тгр, из мест светил проводятся круги равных высот Z₁= 90° – h₁ и Z₂ = 90° – h₂. В одной из точек пересечения место зенита, тогда:

?

где S_м – снимается у кольца меридиана наблюдателя, а S_гр рассчитывается по Т_гр. Широта места равна склонению зенита _z, а долгота = S_м – S_гр .

Графический метод определения места судна на земном глобусе, измеряются высоты h₁ и h₂ двух светил с фиксацией момента Т_гр; из МАЕ выбираются  и t_гр светил, которые являются координатами полюсов освещения. Из полюсов проводятся дуги Z₁= 90° – h₁ и Z₂= 90° – h₂. В одной из точек пересечения дуг будет место судна.

Графическое преобразование координат светила на небесной сфере, позволяет быстро и с достаточной точностью перевести горизонтные координаты светила в координаты первой или второй экваториальной системы и обратно без вычислений по формулам параллактического треугольника. Порядок действий следующий:

1. Построение небесной сферы.

2. Нанесение светила по известным координатам на небесную сферу.

3. Снятие искомых координат светила.

4. Меридиан наблюдателя проводят циркулем, остальные кривые в виде эллипса наносят от руки.

5. Линии на наружной (видимой) части сферы являются сплошными, а линии на внутренней (тыльной) стороне – пунктирными.

6. Ось мира следует проводить с помощью транспортира, зная, что широта места это угол между осью мира и плоскостью истинного горизонта.

7. Дуги, равные координатам, откладывются «на глаз», от центра чертежа к его краям.

Графоаналитический метод определения места судна (метод градиентов), получение места судна не в точке пересечения изолиний, а в точке пересечения касательных к ним вблизи счислимого места в случае двух высотных линий положения или внутри фигуры погрешностей, образованной пересечением касательных, если количество высотных линий положения больше двух. Данные для построения линий вычисляются анали-тически, после чего линии прокладываются на карте, либо на бланке. На первом этапе развития этого метода использовались хорды (Сомнеровы линии), в современной мореходной астрономии – высотные линии положения (ВЛП).

Григорианский календарь, система счисления времени, основанная на циклическом обращении Земли вокруг Солнца. Продолжительность одного цикла принята равной 365.2425 сут; длительность невисокосного года – 365 сут, високосного – 366 сут; содер-жит 97 високосных лет на 400 лет. Распределение високосных годов: год, номер кото-рого кратен 400 – високосный; остальные годы – год, номер которого кратен 100 – невисокосные; остальные годы – год, номер которого кратен 4 – високосный. Таким образом, 1600 и 2000 годы были високосными, а 1700, 1800 и 1900 годы високосными не были. Ошибка в одни сутки по сравнению с годом равноденствий в григорианском кален-даре накопится примерно за 10 000 лет. Впервые григорианский календарь был введён папой римским Григорием XIII в католических странах 4 октября 1582 года взамен старого юлианского: следующим днём после четверга 4 октября стала пятница 15 октя-бря. Поводом к принятию нового календаря стало постепенное смещение по отношению к юлианскому календарю дня весеннего равноденствия, по которому определялась дата Пасхи, и рассогласование пасхальных полнолуний с астрономическими.

Гринвичский меридиан, географический меридиан, проходящий через ось пассажного инструмента Гринвичской обсерватории. Гринвичский меридиан служит началом отсчёта географических долгот с 1884 года, когда на Международной меридианной конференции в Вашингтоне за нуль-пункт отсчёта долгот на всём земном шаре было предложено принять гринвичский меридиан. Является средним меридианом нулевого часового пояса.

Нулевой меридиан в обсерватории Гринвича

Д

Давление света, давление, которое оказывает световое (и вообще электромагнитное) излучение, падающее на поверхность тела. отталкивательное воздействие солнечных лучей на мельчайшие пылевые частицы и на газы, выделяемые кометой при приближении к Солнцу. Происходит формирование так называемого хвоста кометы. Не следует путать понятия «солнечный ветер» (поток ионизированных частиц, долетающий от Солнца до Земли за 2–3 суток) и «солнечный свет» (поток фотонов, долетающий от Солнца до Земли в среднем за 8 минут 17 секунд).

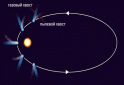
Движение светил для наблюдателя на полюсах и экваторе, на полюсах суточные

параллели светил являются альмукантаратами, все светила со склонениями  одноимен-ными с широтой, движутся параллельно горизонту, половина всех звезд постоянно находится над горизонтом, вторая половина никогда не видна. Полярный день и полярная ночь длятся по полгода.

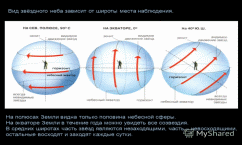
На экваторе суточные параллели перпендикулярны горизонту, за год можно увидеть все звезды.

Декретное время, система исчисления времени «поясное время плюс один час». Применялась с 16 июня 1930 года до 31 марта 1991 года в СССР, с 19 января 1992 года до 27 марта 2011 года в РФ, в настоящее время применяется в ряде стран СНГ.

Т_д = Т_п +1ч

Необходимость перехода мотивировалась более рациональным использованием естест-венного света и перераспределением электроэнергии между бытовым и производ-ственным потреблением. Начиная с 1946 г. декретное время под названием «военное время» было введено во Франции, Бельгии, Голландии, Испании, Монако. По новому закону «Об исчислении времени» понятие декретное время выводится из обращения.

Демаркационная линия (линия смены дат)), условная линия на поверхности земного шара между 12Е и 12W часовыми поясами, по разные стороны которой местное время отличается на сутки. Линия перемены даты примерно соответствует меридиану 180°, проходящему в основном по океану, но местами значительно отклоняется от него.

Линия перемены даты проходит здесь, между островами Диомида – остров Крузенштерна (США) (слева) живёт «вчера», а остров Ратманова (Россия) (справа) – «сегодня»

Смену даты на судах принято производить не в момент перехода, а в полночь, следующую за переходом.

1. При следовании судна восточными курсами с полуночи, следующей за пересечением линии дат, на судне повторяется та же дата, что и была.

2. При следовании западными курсами с полуночи, следующей за пересечением судном линии дат, на судне дата изменяется сразу на две единицы. Изменение даты записывается в судовой журнал.

3. При применении этих правил с момента пересечения 180° меридиана и до следующей полуночи даты сохраняются, а долготы в расчетах считаются сверх 180° в том же направлении. Номер пояса также сохраняется прежним до полуночи.

При кругосветном путешествии с непрерывным счетом дней происходит выигрыш или потеря одних суток – факт, обнаруженный спутниками Магеллана, а также Френсисом Дрейком после возвращение на родину

День весеннего равноденствия, день, когда центр Солнца в своем видимом движении по эклиптике пересекает небесный экватор, переходя из южного полушария в северное. В северном полушарии это 20 или 21 марта. Склонение Солнца 

День летнего солнцестояния, день, когда склонение Солнца . В северном полушарии это 22 июня.

День осеннего равноденствия, день, когда центр Солнца в своем видимом движении по эклиптике пересекает небесный экватор, переходя из северного полушария в южное. В северном полушарии это 22 или 23 сентября. Склонение Солнца 

День зимнего солнцестояния, день, когда склонение Солнца S. В северном полушарии это 22 декабря.

Деферент, понятие, используемое в геоцентрической модели Птолемея. Согласно этой модели, всякая планета равномерно движется по кругу (эпициклу), центр которого, в свою очередь, движется по другому кругу, который и называется деферентом.

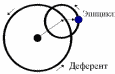
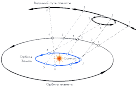
Основанием для такой искусственной конструкции послужила необходимость модели-ровать неравномерное движение планет, в частности, попятное движение, а также объяс-нить изменение их видимой яркости, связанное с изменением расстояния от Земли. Коли-чество деферентов и эпициклов в моделях Птолемея доходило до нескольких десятков.

Диоптры, входящие в комплект секстана металлические угольники, предназначенные для его выверки.

Долгота географическая, угловая координата, определяющая вместе с широтой поло-жение точки на земной поверхности. Измеряется дугой экватора от гринвичского мери-диана до меридиана места, в интервале от 0° до 180° и имеет наименование E или W.

Долгота светила, дуга эклиптики от точки весеннего равноденствия до круга широты светила. Эклиптические долготы отсчитываются в сторону видимого годового движения Солнца по эклиптике, то есть к востоку от точки весеннего равноденствия в интервале от 0° до 360°

Дуга большого круга (ДБК), ортодромия, 1.Кратчайшая линия между двумя точками на поверхности Земли. 2. Наименьший из отрезков дуги большого круга, проходящей через эти точки, часть окружности.

З

Закон всемирного тяготения, между любой парой тел во Вселенной действует сила взаимного притяжения. Если M и m – массы двух тел, а R – расстояние между ними, тогда F = gMm/R2,

где g – гравитационная константа, определяемая экспериментально. В единицах СИ ее значение составляет g = 6,67.10^-11.

Законы Кеплера,

1-й закон, орбита планеты есть эллипс, в одном из фокусов которого (общем для всех планет) находится Солнце.

2-й закон, радиус-вектор R планеты в равные времена описывает равные S площади,

S₁ = S₂. Следствие закона – неравномерность движения планеты по орбите. Эта нерав-номерность объясняется: а) эллиптичностью орбиты и б) наклоном земной оси к плоскости эклиптики.

1-й закон 2-й закон 3-й закон

3-й закон, квадраты сидерических (звездных) периодов обращений планет вокруг Солнца относятся, как кубы больших полуосей их орбит. Следствие закона – уменьшение лине-йной скорости движения планеты по орбите по мере удаления от Солнца.

Затмение Луны, прохождение Луны через конус земной тени, отбрасываемой Землёй. Затмение Луны может быть полным, частным или полутеневым. Лунное затмение видно на всем ночном полушарии Земли и для всех точек этого полушария начинается и закан-чивается одновременно. На протяжении года может произойти ни одного лунного затмения, а самое большое количество их три. Очевидно, что затмения Луны могут происходить только во время полнолуний.

Лунное затмение

Затмение Солнца, закрытие диска Солнца диском Луны.

Диск Солнца будет закрыт целиком только для наблюдателя, находящегося внутри конуса лунной тени, наибольший диаметр которого на поверхности Земли не превосходит 270 км, в областях полутени видно частное затмение. Из-за эллиптичности лунной орбиты вершина конуса иногда находится над поверхностью Земли, угловые размеры диска Луны при этом меньше углового размера диска Солнца и затмение будет кольцеобразным. За год может произойти самое большее 7 затмений – либо 2 лунных и 5 солнечных, либо 3 лунных и 4 солнечных. Чаще всего в году бывает 2 солнечных и 2 лунных затмения. Краткие сведения о затмениях приводятся в МАЕ на 24 странице.

Полное солнечное Частное солнечное Кольцеобразное

затмение затмение солнечное затмение

Звездная величина m, безразмерная числовая характеристика яркости объекта, чем меньше значение числа звёздной величины, тем больше блеск данного объекта. Этот термин ввел Гиппарх во II веке до нашей эры. Самым ярким звездам Гиппарх присвоил первую звездную величину, а самым тусклым, едва видимым глазом, – шестую. При этом звезды 2-й величины считались во столько раз слабее звезд 1-й, насколько звезды 3-й величины слабее звезд 2-й и т.д. Звезда 1-й звёздной величины ярче звезды 6 звёздной величины примерно в 100 раз. В древности люди полагали, что звезды находятся на небесной сфере на одном расстоянии от Земли, поэтому различие в яркости звезд объяснялось различием в их реальных размерах или величине. Если светила более яркие, чем звезды нулевой величины, их звездная величина отрицательна: зв. вел. Солнца –26.7, Луны –12.7, Венеры m = – 4.7, Марса m = –2.9, Юпитера m = –2.9, Полярной звезды m = +2.2, Сириуса m = –2.7. Невооруженным глазом на небе можно наблюдать около шести тысяч звезд, самые слабые звезды имеют звездную величину от+6 до +7.7. Самый далёкий астрономический объект имеет звездную величину +49.8.

Звездное время S, время, протекшее от момента верхней кульминации точки Овна до данного момента, оно измеряется часовым углом точки весеннего равноденствия. Звездное время зависит от вращения Земли, и, следовательно, шкала звездного времени является неравномерной. Звездное время не имеет даты. В МАЕ звездное время представлено в левой колонке левого разворота ежедневных таблиц.

Звездный год, время, за которое Солнце совершает полный оборот относительно напра-вления на выбранную неподвижную звезду–сидерический год. Т_зв = 365,25636 сут. Звездные сутки, интервал времени между двумя последовательными верхними кульми-нациями точки Овна на одном и том же меридиане; звёздные сутки, на 3^мм56^с короче средних солнечных суток – в этом причина изменения вида звездного неба в данной широте в течении года.

Звездный глобус, модель небесной сферы, предназначенная для приближенного реше-ния задач мореходной астрономии: опознания светила, подбора светил для наблюдений и снятии координат и светил. Глобус устанавливается по широте и местному звездному времени S_м. Повышенный полюс Р_N (Р_S) ставится над точкой N (S) азимутального круга. Под кольцо меридиана наблюдателя подводится величина S_м.

Звездный глобус

1 – полюс, 2 – экватор, 3 – меридиан, 4 – кольцо меридиана наблюдателя, 5 – параллель, 6 – зенит, 7 – истинный горизонт, 8 – крестовина вертикалов, 9 – эклиптика. После ус-тановки глобуса по широте наблюдателя и местному звездному времени наблюдений ме-ридиональное кольцо соответствует меридиану наблюдателя.

1. Установка глобуса по широте места. Развернуть меридиональное кольцо так, чтобы одноименный с широтой места повышенный полюс мира находился над одноименной точкой истинного горизонта. Для установки высоты полюса равной широте места,

поворачивая мери диональное кольцо, подвести отсчет на его боковой шкале равный широте места на уровень истинного горизонта. Глобус установлен по

 = 25.3°N.

Установка по широте места

2. Установка глобуса по звездному местному времени. Поворачивая глобус вокруг оси мира, подвести отсчет шкалы небесного экватора равный S_м к оцифрованной стороне меридионального кольца. Проверить установку глобуса по широте места.

На рисунке звездный глобус установлен по S_м = 311.2°.

Правильно установленный звездный глобус дает картину звездного неба в данной счислимой точке в данное время.

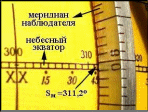
Установка по местному звездному времени

Звезды, излучающие свет массивные газовые шары, удерживаемые силами собственной гравитации, в недрах которых происходят реакции термоядерного синтеза, находящиеся на громадных расстояниях друг от друга. Если в солнечной системе за единицу рас-стояния принята астрономическая единица (1а.е.= 149 600 000 км), равная среднему рас-стоянию от Земли до Солнца, то в межзвездной среде используютя иные единицы: свето-вой год, парсек, килопарсек и т.д. Один св.год = 9.5.10¹²км. Один парсек = 206 265 а.е.= 3.26 св.лет. Свет от Солнца достигает Земли за 8 минут, от самой удаленной планеты солнечной системы – Плутона – за 5 часов, от ближайшей звезды – Центавра за 4.5 года. Размеры звезд различны: от белых карликов с диаметром втрое меньшим земного, до гигантов с диаметром в 1000 раз больше солнечного.

В 1922 г. все звезды были распределены по 88 созвездиям. Созвездия разнообразны и по площадям, занимаемым ими на небе, и по количеству звезд, и по их рисунку, обра-зуемому звездами. Наиболее яркие звезды в созвездии принято обозначать буквами гре-ческого алфавита в порядке уменьшения блеска, некоторые звезды имеют собственное имя. 160 наиболее ярких звезд выбраны в качестве навигационных, им присвоены номера от 1 до 160. Звезды различаются по видимому блеску, который оценивается видимой звездной величиной m. Самые яркие относятся к звездам первой величины, самые слабые – к шестой. Блеск звезды каждой последующей величины в 2.5 раза слабее блеска звезды данной величины. Есть светила более яркие, чем звезды первой величины, их звездная величина отрицательна: Солнце –26.8m, Луна в полнолунии –12.6m, Венера в максимальном блеске –4.4m, самая яркая звезда неба Сириус –1.6m. Принято называть звезду так: Ориона = альфа Ориона = Бетельгейзе = № 40. Солнце входит в систему около 300 млрд звезд, называемую Галактикой, по форме похожую на плоский диск с шарообразным утолщением в центре. Диаметр диска около 30 килопарсек, толщина – около 4. Солнце находится на расстоянии 26 000 св.лет от ее центра. Большая часть Галактики представлена на небе Млечным путем. Часть звезд объединена в шаровые и рассеянные звездные скопления, межзвездная среда заполнена облаками космической пыли и газа. Звезды бесконечно разнообразны по величине, химическому составу, температуре и т.д. Звезды кратные, переменные, карлики, супергиганты, пульсары, нейтронные, сверхновые, черные дыры... . Наша Галактика соседствует с несколькими галактиками: туманностью Андромеды, Большим и Малым Магеллановым облаками и рядом других, вместе с которыми она образует Местную группу галактик диаметром 3·10⁶ св.лет. Обнару

жено около миллиарда внегалактических объектов аналогичных нашей звездной системе. Галактики, как и звезды, объединяются в группы и скопления. Например, в созвездии Волос Вероники насчитывается около 40 000 галактик – спиральных, эллиптических, неправильных. Галактики являются источниками радиоизлучения, изучено около 2000 вза-имодействующих галактик. Квазары, квазаги, N-галактики – все новые и новые обнару-живаемые объекты, находящиеся на расстоянии до 12 млрд. св.лет – на пределе современ-ных представлений о границах изучаемого мира. Вот на таком грандиозном фоне судово-дитель решает свои основные задачи – определения места судна и поправки компаса.

Звезды двойные, две гравитационно-связанные звезды, обращающиеся по замкнутым орбитам вокруг общего центра масс. Около половины всех звёзд нашей Галактики принадлежит к двойным системам. Примером двойной звезды является система Мицар – Алькор: Мицар – звезда в созвездии Большой Медведицы, вторая от конца ручки большого «ковша».

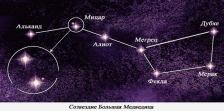
На самом деле, обе звезды входят в физически связанную систему, состоящую из 6 звёзд: двойные звезды Мицар А и Мицар В, и лежащая на расстоянии около 0.3 световых лет от них двойная звезда Алькор (около 12 угловых минут). Существует легенда, что в древнем Египте в элитные войска фараона набирали юношей, которые могли различать эти звезды. Это было доказательством, что зрение было достаточно острым. Способность видеть Алькор – традиционный способ проверки зрения. Двойными могут быть звезды, случайно оказавшиеся почти на одном луче зрения, никак физически не связанные между собой. Они называются оптически-двойными. Обнаружены звезды и большей кратности.

Звезды навигационные 160 звезд в МАЕ, используемых для определения места судна и поправки компаса. Для 72 звезд видимые места – звездные дополненияи склонения даны на правом развороте ежедневных таблиц МАЕ, видимые места 160 звезд даны на стр. 270 – 275 МАЕ.

Звезды видимые, условие восхода и захода светила в данной широте независимо от наименования –

Звезды невосходящие невидимые в данной широте звезды, чьи суточные параллели проходят ниже уровня горизонта. Условие этого: –причем и – разно-именны

Звезды незаходящие видимые в данной широте звезды, чьи суточные параллели про-ходят выше уровня горизонта. Условие этого: –причем и – одноименны

Зеленый луч редкое оптическое явление. Вспышка зелёного света в момент захода/восхода Солнца.

Обычная продолжительность зелёного луча несколько секунд. Можно значительно увели-ить время его наблюдения, если при его появлении быстро переходить с одной палубы суд-на на другую с такой скоростью, чтобы сохранить положение глаза относительно зелёного луча.

Земля третья от Солнца планета солнечной системы, на среднем расстоянии 1а.е., с пе-риодом обращения в 1 год, полярный радиус 6356.9 км, экваториальный 6378.17 км, период осевого вращения относительно звезд 23^ч56^м04.1^с . Земля отличается от всех дру-гих планет Солнечной системы наличием гидросферы и биосферы, а такие большой ди-намической активностью коры и атмосферы. У Земли один естественный спутник – Луна.

На снимке из космоса Земля и Луна.

Земная ось, (ось вращения Земли), воображаемая линия, вокруг которой происходит суточное вращение Земли; проходит через центр Земли и пересекает земную поверхность в географических полюсах 

Зенит одна из двух точек пересечения отвесной линии с небесной сферой.

Зенитное расстояние дуга вертикала от зенита до светила. Изменяется от 0° до 180°.

z + h = 90°. Меридиональное зенитное расстояние

Z = 90° – Н

Z имеет наименование противоположное наименованию Н, а Н имеет наименование точки полуденной линии, над которой она измерена, а именно N или S. Использование наименования меридионального зенитного расстояния Солнца применялось при опреде-лении широты по измерениям высоты Солнца в местный полдень.

Зенитомерприбор, предназначенный для прямого определения координат зенита, с последующим получением места судна по соотношениям:

_z, и t_гр .

Применение приборов требует сложных систем стабилизации судна и отслеживания светила, поэтому на транспортном флоте они не используются. Разработаны – «Зенитомер» А.А.Михайлова (1944г.), «Ночной определитель места» Л. Рандича (1956г.), «Двухзвездный секстан» Хогга и др.

Знаки зодиака 12 секторов по 30°, на которые разделен зодиакальный пояс в евро-пейской астрологической традиции; это деление восходит к вавилонской шестидеся-теричной системе счисления и астрономии, в которой небесный круг делился на 360 угловых долей, что примерно соответствует количеству дней в году. Из-за прецессии знаки в наше время не совпадают с одноименными созвездиями.

Зодиак пояс на небесной сфере вдоль эклиптики, по которому проходят видимые пути Солнца, Луны и планет. При этом Солнце движется практически строго по эклиптике, а остальные светила в своём движении по зодиаку периодически смещаются севернее или южнее эклиптики в зависимости от текущего положения узлов своих орбит до максимального расстояния, равного их наклонению. Эклиптическое наклонение орбит Луны и видимых планет не превышает нескольких градусов, традиционно ширина зодиакального пояса считается условно равной 9° в обе стороны от эклиптики.

Зодиакальный свет слабое свечение, наблюдающееся вскоре после захода или перед восходом Солнца (сразу по окончании или непосредственно перед началом астро-номических сумерек).

Зодиакальные созвездия: Овен, Телец, Близнецы, Рак, Лев, Дева, Весы, Скорпион, Стрелец, Козерог, Водолей, Рыбы, по которым перемещается Солнце в своем видимом движении по эклиптике. Изначально зодиакальных созвездий было 13. Солнце, прежде чем оказаться в созвездии Стрельца, проходит через созвездие Змееносца в течении нескольких дней с 30 ноября по 18 декабря, но, так как зодиакальных созвездий должно быть двенадцать, по числу месяцев в году, его не включают в Зодиак. И как быть с гороскопами людей, родившихся в этом временном интервале?

И

Изменение азимута в суточном движении,

А = – (sin – tgh·cosA·cos)t .

Иследование этой формулы приводит к следующим выводам:

1. Она состоит из двух частей: A₁ = – sint, одинаковой для всех светил и независимой от положения светила на сфере и A₂= – cos · соsA·tg ht, зависящей и от , и от , и от самого азимута, т.е. от положения светила.

2. A₁ обращается в 0 лишь для наблюдателей на экваторе, для наблюдателей на полюсе A₁ = –t.

3. Независимо от широты, A₂=0 при двух положениях светила: на 1-м вертикале (cos А = 0) и при восходе, заходе светила (tg h = 0), и в обоих этих случаях

A = A₁ = – sin t.

4. Для моментов кульминаций A = ± cos ·sec ht.

5. Видно, что азимут лишь на восходе, заходе и у 1-го вертикала изменяется равномерно, во всех других положениях светила изменение его азимута происходит неравномерно. Быстрее всего азимут меняется около верхней кульминации, медленнее всего азимут меняется от восхода до 1-го вертикала, а в элонгации – не меняется.

6. На экваторе и в тропиках азимут меняется крайне неравномерно – от 0° до мгновенного (h = 90°), а на полюсе равномерно, так же , как t.