ОГЛАВЛЕНИЕ

1. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ СХЕМЫ ЗАМЕЩЕНИЯ ВОЗДУШНОЙ ЛИНИИ ЭЛЕКТРОПЕРЕДАЧИ В ФАЗНЫХ И СИММЕТРИЧНЫХ КООРДИНАТАХ И ОПРЕДЕЛЕНИЕ МЕСТА ПОВРЕЖДЕНИЯ ВЛ 3

1.1. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ СХЕМЫ ЗАМЕЩЕНИЯ ОДНОЦЕПНОЙ ВЛ С ДВУМЯ ТРОСАМИ 3

1.2. ОПРЕДЕЛЕНИЕ МЕСТА ПОВРЕЖДЕНИЯ НА ВЛ «БАЯНДАЙ – КАЧУГ» ПО ДВУХСТОРОННИМ ИЗМЕРЕНИЯМ ЗНАЧЕНИЙ ТОКОВ И НАПРЯЖЕНИЙ НУЛЕВОЙ И ОБРАТНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ С ИСПОЛЬЗОВАНИЕМ СИСТЕМЫ MATHCAD 13

1.2.1. Расчетные параметры линии определённые через среднегеометрические значения промежуточной опоры 13

1.2.2. Параметры линии, введенные в регистратор (ЦРАП) 13

1.2.3. Исходные данные параметров короткого замыкания в фазных координатах 14

1.2.4. Определение симметричных составляющих параметров аварийного режима 15

1.2.5. Определение места повреждения 17

2. РАСЧЕТ УСТАНОВИВШИХСЯ РЕЖИМОВ ВЛ 18

2.1. ЗАДАНИЕ 18

2.2. ИСХОДНЫЕ ДАННЫЕ 18

2.3. СХЕМА ЗАМЕЩЕНИЯ 18

2.4. ВВОД ИСХОДНЫХ ДАННЫХ В ЭВМ 20

2.5. УСТАНОВКА НА РАСЧЕТ. РАСЧЕТ РЕЖИМА 20

2.6. ПРОТОКОЛ РАСЧЕТА 21

2.7. РЕЗУЛЬТАТЫ РАСЧЕТА В ФОРМЕ ТАБЛИЦ 21

2.8. КАРТА РЕЖИМА 22

2.9. ОПРЕДЕЛЕНИЕ ДОПОЛНИТЕЛЬНЫХ ПАРАМЕТРОВ В ЭЛЕМЕНТАХ СЕТИ 22

3. РАСЧЕТ НАСИММЕТРИЧНЫХ РЕЖИМОВ ЭЭС С ИСПОЛЬЗОВАНИЕМ УРАВНЕНИЙ КОНТУРНЫХ ТОКОВ И ФАЗНЫХ КООРДИНАТ 25

3.1. ЗАДАНИЕ 25

3.2. ИСХОДНЫЕ ДАННЫЕ 25

3.3. СХЕМА ЗАМЕЩЕНИЯ ЭЭС 25

3.4. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДЛЯ РАСЧЕТА РЕЖИМОВ ЭЭС 26

3.5. РАСЧЕТ ТОКОВ В ЗАДАННЫХ РЕЖИМАХ ЭЭС 27

3.5.1. Симметричный режим 27

3.5.2. Несимметричный режим 30

3.5.3. Обрыв фазы 33

3.5.4. Однофазное КЗ 36

3.5.5. Двухфазное КЗ 39

3.6. КАРТА ТОКОВ В ЗАДАННЫХ РЕЖИМАХ ЭЭС 42

3.7. ВЕКТОРНЫЕ ДИАГРАММЫ ТОКОВ 43

ЛИТЕРАТУРА 46

1. Определение параметров схемы замещения воздушной линии электропередачи в фазных и симметричных координатах и определение места повреждения вл

1.1. Определение параметров схемы замещения одноцепной вл с двумя тросами

Рисунок 1. Расположение проводов на опоре

А-земля___ _18.500 м

В-земля____12.000 м

С-земля____12.000 м

А-В________11.265 м

В-С________11.800 м

А-С_________7.000 м

А-А’__ ____37.000 м

В-В’_______24.000 м

С-С’_______24.000 м

А-В’_______31.857 м

А-С’_______30.601 м

В-С’_______26.744 м

Т1-земля 23.500 м

Т1-А 6.000 м

Т1-В 12.925 м

Т1-С 12.925 м

Т1-Т1’ 47.000 м

Т1-А’ 42.130 м

Т1-В’ 35.987 м

Т1-С’ 35.987 м

Т2-земля 23.500 м

Т2-А 6.000 м

Т2-В 12.925 м

Т2-С 12.925 м

Т2-Т2’ 47.000 м

Т2-А’ 42.130 м

Т2-В’ 35.987 м

Т2-С’ 35.987 м

Т1-Т2 2.000 м

Т1-Т2’ 50.000 м

Рассчитать сопротивления линии длиной 10 км, для тока промышленной частоты (f = 50 Гц). Марка провода АС-300/66. Тросы марки С-70 заземлены с одного края и находятся через искровой промежуток от земли с другого края. Транспозиция отсутствует. Стрелой провеса проводов пренебречь.

Решение:

Удельное активное сопротивление провода марки АС-300/66

R_п = 0.102 Ом/км.

Радиус провода марки АС-300/66

_П = 12.5*10^-3 м.

Эквивалентный радиус провода

м.

Удельные собственные продольные сопротивления фазного провода, Ом/км:

.

Удельные взаимные продольные сопротивления, Ом/км:

;

;

.

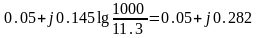Матрица погонных продольных сопротивлений линии, Ом/км:

.

Матрица продольных сопротивлений линии длиной 10 км, Ом:

.

Матрица погонных продольных сопротивлений линии в симметричных координатах, Ом/км:

;

.

Недиагональные элементы получившейся матрица не равны нулю.

Определим среднее расстояние между фазными проводами:

м.

Подставив D_ср вместо D_ij, получим:

Ом/км.

Подставив это значение, получим:

матрица погонных продольных сопротивлений линии в ФК, Ом/км:

.

Матрица погонных продольных сопротивлений линии в симметричных координатах, Ом/км:

.

В полученной матрице все недиагональные элементы нулевые.

Определим продольные погонные сопротивления прямой, обратной и нулевой последовательностей:

Из вышеизложенных расчетов видно, что продольные сопротивления в СК, полученные по D_ср и по формулам, совпадают. Для получения сопротивлений 10 км линии необходимо матрицы погонных продольных сопротивлений линии увеличить в 10 раз.

Рассчитаем поперечные погонные сопротивления данной линии. Находим погонные потенциальные коэффициенты :

км/нФ ;

км/нФ;

км/нФ ;

км/нФ;

;

км/нФ;

;

.

Составляем матрицу погонных потенциальных коэффициентов, км/нФ:

.

Определяем матрицу погонных емкостных коэффициентов , нФ/км:

.

Определяем погонные частичные емкости:

С_АА =₁₁+₁₂+₁₃+₁₄+₁₅=7.76 – 0.63 – 1.128 – 1.175 – 1.148= 3.679 нФ/км;

С_ВВ =₂₁+₂₂+₂₃+₂₄+₂₅₌ - 0.63 + 7.588 – 0.557 – 0.534 -0.497 =5.37 нФ/км;

С_СС =₃₁+₄₂+₃₃+₃₄+₃₅= - 1.128 - 0.557 + 7.701 – 0.458 -0.423 = 5.135 нФ/км;

С_Т1Т1 =₄₁+₄₂+₄₃+₄₄+₄₅= -1.175 – 0.534 – 0.458 + 8.319-2.872 = 3.28 нФ/км;

С_Т2Т2 =₅₁+₅₂+₅₃+₅₄+₅₅= -1.148 – 0.497 – 0.423 -2.872 + 8.297 = 3.357 нФ/км;

С_АВ = С_ВА = ₁₂=₂₁=-0.63 нФ/км;

С_АС = С_СА = ₁₃=₃₁=-1.128 нФ/км;

С_ВС = С_СВ = ₂₃=₃₂=-0.557 нФ/км;

С_АТ1 = С_Т1А = ₁₄=₄₁=-1.175 нФ/км;

С_АТ2 = С_Т2А = ₁₅=₅₁=-1.148 нФ/км;

С_ВТ1 = С_Т1В = ₂₄=₄₂=-0.534 нФ/км;

С_ВТ2 = С_Т2В = ₂₅=₅₂=-0.497 нФ/км;

С_СТ1 = С_Т1С = ₃₄=₄₃=-0.458 нФ/км;

С_СТ2 = С_Т2С = ₃₅=₅₃=-0.423 нФ/км;

С_Т1Т2 = С_Т2Т1 = ₄₅=₅₄=-2.872 нФ/км.

Определим поперечные емкости для линии длиной 10 км:

;

;

Определим поперечные емкости в симметричных координатах.

Определим :

Определим и :

Определим собственные и взаимные погонные потенциальные коэффициенты

км/нФ;

км/нФ.

Полученная матрица погонных потенциальных коэффициентов, км/нФ:

.

Определим эквивалентную матрицу .

Представим матрицу в виде составной матрицы, состоящей из следующих блоков, км/нФ:

;

;

;

.

Определим эквивалентную матрицу , км/нФ:

.

Определим матрицу погонных емкостных коэффициентов _ср , нФ/км:

.

Полученную матрицу переводим в СК:

Матрица погонных емкостных коэффициентов в СК, нФ/км:

.

Погонные емкости линии нулевой, прямой и обратной последовательностей:

нФ/км;

нФ/км;

нФ/км.

Отсюда, искомые емкостные сопротивления и поперечные проводимости нулевой, прямой и обратной последовательностей линии длиной 10 км соответственно составляют:

Матрица емкостные поперечных сопротивлений нулевой, прямой и обратной последовательностей линии длиной 10 км, МОм:

.