
- •Лекция № 13
- •4. Динамическое программирование
- •4.1.1.1. Задачи с одним типом управлений и одним ограничением (здп 1)
- •4.1.1.2. Задачи с одним типом управлений и двумя ограничениями (здп2)
- •4.1.1.3. Задачи с двумя типами управлений и двумя ограничениями (здп3)
- •4.1.2. Детерминированные задачи последовательного принятия решений
- •4.2. Применение метода динамического программирования к здп 1
- •4.2.1. Решение дискретной задачи
- •Лекция №15
- •4.3. Применение метода динамического программирования к здп 2
- •4.4. Применение метода динамического программирования к здп 3
- •4.7. Свойства метода динамического программирования
4.1.2. Детерминированные задачи последовательного принятия решений
Общая содержательная постановка задачи последовательного принятия решений.
Рассматривается n-шаговый управляемый процесс. Под шагом понимается переход процесса из одного состояния в другое. Состояние процесса определяется конечным числом переменных состояния. Детерминированный характер процесса определяет следующее его свойство: состояние процесса после каждого шага определяется однозначно предыдущим состоянием и выбранным на данном шаге управлением (рис.4.1) Всегда считается известным начальное состояние процесса. По необходимости обеспечить определенное конечное состояние процесса детерминированные задачи последовательного принятия решений (ДЗППР) разделяются на два подкласса: задачи с незакрепленным и закрепленным конечным состоянием.
Выбор управления на каждом шаге осуществляется из заданного множества альтернатив, которое может быть связано с текущим состоянием, или из некоторого допустимого множества, определяемого действующими в текущем состоянии ограничениями.
Целевая функция оптимизационной задачи определяется суммой компонент по шагам процесса, зависящих в общем случае от состояний этого процесса в начале и в конце шага и выбранного на данном шаге управления. Направление оптимизации определяется сущностью рассматриваемой задачи.
В отличие от задач динамического программирования типа распределения ресурсов в ДЗППР логическая последовательность шагов однозначно определяется сущностью конкретной рассматриваемой задачи и не может быть изменена в процессе ее решения.
Обобщенная формальная запись ДЗППР может быть представлена в следующем виде:
а)
для задач с незакрепленным конечным
состоянием (задано лишь начальное
состояние
![]() )
)
![]() , (4.8)
, (4.8)
б)
для задач с закрепленным конечным
состоянием (задано и начальное состояние
и конечное состояние
![]() )
)
![]() . (4.9)
. (4.9)
Примерами названий задач, которые формализуются в виде ДЗППР, могут быть следующие:
- о нахождении маршрута на транспортной сети из одного пункта в другой, соответствующего минимуму времени движения (или затрат топлива транспортного средства);
об определении критического (наиболее продолжительного) пути в сетевом графе комплекса работ;
об управлении жизненным циклом системы (принятии последовательности решений по поддержанию работы созданного варианта системы, его модернизации, снятия с эксплуатации и замены новым, более совершенным вариантом) с целью максимизации интегральной прибыли, получаемой в результате функционирования рассматриваемой системы;
о формировании траектории ЛА из заданного множества типовых участков для вывода его в определенную точку пространства за минимальное время или с минимальным расходом топлива;
об использовании рабочей силы при выполнении многоэтапной программы работ и многие другие.
4.2. Применение метода динамического программирования к здп 1
4.2.1. Решение дискретной задачи
В случае дискретной задачи (x[j] Î N, (j=1,2,..n) ЗДП I должна быть приведена к виду, где a[j] (j=1,n) и b являются целыми положительными числами.
Условие целочисленности коэффициентов a[j] и b не уменьшает общности задачи, так как его выполнение всегда может быть достигнуто с любой степенью точности. По существу сделанное предположение определяет лишь выбор единиц измерения величин a[j] и b.
Применение метода динамического программирования связано с необходимостью определения для рассматриваемой задачи функции Беллмана и вывода рекуррентного соотношения для нахождения ее значений.
Функция Беллмана всегда определяется как часть исходной задачи, аналогичная ей по записи.
В
ЗДП I
функция
Беллмана
![]() (ее еще называют функцией
состояния)
определяется как максимум суммы k
первых компонент целевой функции
(k=1,2,…,n)
по первым k
компонентам управлений при выделении
на их реализацию ресурса величиной
(ее еще называют функцией
состояния)
определяется как максимум суммы k
первых компонент целевой функции
(k=1,2,…,n)
по первым k
компонентам управлений при выделении
на их реализацию ресурса величиной
![]() (в терминологии динамического
программирования это - переменная
состояния,
принимающая только целочисленные
значения
=0,1,2,…,b):
(в терминологии динамического
программирования это - переменная
состояния,
принимающая только целочисленные
значения
=0,1,2,…,b):
![]() . (4.12)
. (4.12)
Сравним с записью исходной задачи:
![]() =
{z
=
fj
(x[j])};
a[j]x[j]
£
b; x[j]
Î
N,
(j=1,2,..n), (4.1)
=
{z
=
fj
(x[j])};
a[j]x[j]
£
b; x[j]
Î
N,
(j=1,2,..n), (4.1)
Видим, что задача определения значения функции Беллмана является аналогичной по своей структуре исходной задаче, только в общем случае с меньшим числом компонент целевой функции и, соответственно, - управлений и меньшей величиной распределяемого ресурса.
В частном случае из (4.12) следует, что максимальное значение целевой функции всей задачи
![]() . (4.13)
. (4.13)
Для
общности будем полагать, что
![]() для всех
.
для всех
.
Осуществим вывод рекуррентного соотношения для нахождения значений этой функции при различных значениях k и .
Сначала зафиксируем компоненту x[n] и определим максимум целевой функции по всем другим x[j] (j=1,2,…,n-1) с учетом ограничения исходной задачи:
![]() z
=
{fn(x[n])+
z
=
{fn(x[n])+![]()
![]() fj(x[j])},
a[j]x[j]
£
b–a[n]x[n]
(3.14)
fj(x[j])},
a[j]x[j]
£
b–a[n]x[n]
(3.14)
Исходя из определения (4.12), часть соотношения (3.14), находящуюся под оператором max, с учетом ограничения на переменные x[j] (j=1,2,…,n-1) можно переписать в следующем виде:
{fn(x[n])+![]() }. (4.15)
}. (4.15)
Тогда можно утверждать, что
=
![]() {fn(x[n])
+ Ln-1(b-a[n]x[n])}, (4.16)
{fn(x[n])
+ Ln-1(b-a[n]x[n])}, (4.16)
где [b/a[n]] – целая часть отношения b/a[n] (максимальное значение переменной x[n], когда весь ресурс b будет расходоваться на реализацию только этой переменной), а задача нахождения максимума решается перебором по возможным целочисленным значениям x[n] в указанных пределах.
Соотношение
(4.16) имеет относительно функции Беллмана
рекуррентный
характер. Чтобы
определить в нем максимум по х[n]
необходимо знать значения
![]() для различных значений
=b-a[n]x[n].
Так как задача определения
аналогична по своей структуре исходной
задаче, то для ее решения можно применить
тот же подход:
для различных значений
=b-a[n]x[n].
Так как задача определения
аналогична по своей структуре исходной
задаче, то для ее решения можно применить
тот же подход:
сначала зафиксировать переменную x[n-1], а затем решить по ней следующую задачу оптимизации:
Ln-1(x)
=
![]() {
fn-1(x[n-1])
+ Ln-2(x-a[n-1]x[n-1])} (4.17)
{
fn-1(x[n-1])
+ Ln-2(x-a[n-1]x[n-1])} (4.17)
Продолжая действовать таким же образом и дальше, с использованием метода математической индукции получим следующее общего вида рекуррентное соотношение для функции Беллмана:
Lj(x)
=
![]() {fj(x[j])
+ Lj-1(x-a[j]x[j])}, (4.18)
{fj(x[j])
+ Lj-1(x-a[j]x[j])}, (4.18)
где [x/a[j]] – целая часть отношения x/a[j], определяющая условие выполнения ограничения по ресурсу в предельном случае, когда вся его величина x будет израсходована только на управление x[j].
Значение x[j], доставляющее соотношению (4.18) максимум и определяемое перебором по указанным под оператором max возможным значениям, называют условно оптимальным управлением и хранят в таблице х[x,j]. Условным оно называется потому, что вычисляется при условии выделения на первые j компонент управлений ресурса величиной x.
Из
всех условно оптимальных управлений
только одно x[b,n]
очевидным образом совпадает с безусловно
оптимальным управлением
![]() ,
так как известно, что на
все управления
будет использован весь
ресурс b.
,
так как известно, что на
все управления
будет использован весь
ресурс b.
Решение ЗДП I с помощью рекуррентного соотношения (4.18) осуществляется в два этапа.
Этап 1. Определение значений функции Беллмана и условно оптимальных управлений в виде дух таблиц Lj(x) и х[x,j] (рис. 4.4, строки в этих таблицах соответствуют значениям x, а столбцы – значениям j):
1.1) для j=1,2,…,n-1 и x=0,1,2,…,b,
т.е. заполнение таблиц осуществляется по столбцам (сначала –первый, затем второй столбец и т.д. При расчете L1(x) в соответствии с рекуррентным соотношением полагают L0(x)=0 для всех x, т.е. решается задача:
L1(x)
=
![]() {f1(x[1])},
{f1(x[1])},
1.2) для j=n и x=b (при этом определяются и = x[b,n]).
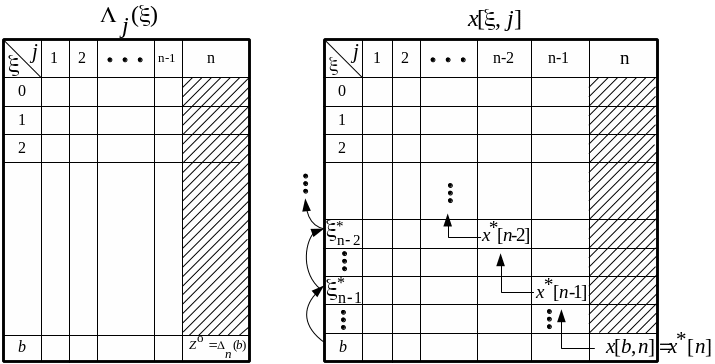
Рис. 4.4.
Этап 2. Определение всех остальных безусловно оптимальных управлений обратным ходом по таблице условно оптимальных управлений (один шаг поясним подробно, а остальные приводятся без пояснений по аналогии):
расчет величины ресурса, оставшегося в оптимальном плане на первые n-1 компоненты управлений:
![]()
![]() ;
;
- выбор из таблицы условно оптимальных управлений значения безусловно оптимального управления по (n-1)-ой компоненте:
![]() ;
;
для определения безусловно оптимального управления по (n-2)-ой компоненте:
![]() ,
,
![]() ;
;
….
для определения безусловно оптимального управления по j - ой компоненте:
![]() ,
,
![]() ; (4.19)
; (4.19)
далее по аналогии расчеты делаются для j-1, j-2,…, 1.
ЛЕКЦИЯ № 14
4.2.2. Решение задачи с управлениями, принимающими действительные значения
Вид рекуррентного соотношения для этого случая отличается от соответствующего соотношения для дискретной задачи (4.18) только записью ограничения сверху на выбор управления x[j] в операции max: здесь ненужно выделять целую часть отношения x/a[j]:
Lj(x)=![]() {fj(x[j])+Lj-1(x-a[j]x[j])} (4.20)
{fj(x[j])+Lj-1(x-a[j]x[j])} (4.20)
Но с использованием его для решения задачи связан целый ряд проблем. Рассмотрим каждую из них подробно.
Проблема
табулирования функции Lj(x)
по x
и вычисления ее значений в точках, где
табуляция отсутствует.
Эта проблема связана с тем, что в
рекуррентном соотношении (4.20) переменная
состояния x
может принимать любые неотрицательные
значения. Табуляция может быть осуществлена
с некоторым шагом
![]() ,
выбор значения которого определяется
желаемой точностью распределения
ресурса. При этом для вычисления значений
функции Lj-1(x-a[j]x[j])
в точках, в которых табуляция отсутствует,
естественно использовать метод линейной
интерполяции по соседним табулированным
точкам. Но использование метода линейной
интерполяции накладывает дополнительные
ограничения на вид функций fj(x[j]):
они должны быть непрерывными.
,
выбор значения которого определяется
желаемой точностью распределения
ресурса. При этом для вычисления значений
функции Lj-1(x-a[j]x[j])
в точках, в которых табуляция отсутствует,
естественно использовать метод линейной
интерполяции по соседним табулированным
точкам. Но использование метода линейной
интерполяции накладывает дополнительные
ограничения на вид функций fj(x[j]):
они должны быть непрерывными.
Проблема
решения задачи оптимизации при определении
значений функции
Беллмана: ![]() {Wj(x[j],x)=fj(x[j])+Lj-1(x-a[j]x[j])}.
{Wj(x[j],x)=fj(x[j])+Lj-1(x-a[j]x[j])}.
Эту задачу здесь нельзя решить путем перебора целочисленных значений x[j], как в дискретной задаче, а необходимо решать как общую задачу одномерной (возможно, многоэкстремальной) оптимизации. Известно, что разработаны эффективные алгоритмы одномерной оптимизации только для унимодальных функций (см. раздел 2.2.1., 2.2.2.)
При общем виде функции можно, например, рекомендовать к использованию способ максимизации, работа которого показана на рис.4.4.
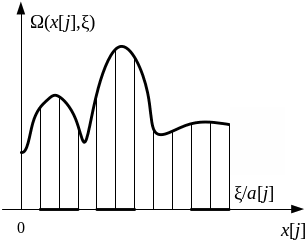 Рис.
4.4.
Рис.
4.4.
Проводится ряд итераций по вычислению значений функции Wj(x[j],x) в точках сетки, формируемой итеративно с постепенно уменьшающимся шагом по x[j]: сетка с меньшим шагом формируется в окрестностях предполагаемых локальных максимумов. На заключительном этапе в выявленных конкурирующих между собой районах локальных максимумов может быть применен один из методов поиска экстремума унимодальной функции.
В двух частных, но достаточно часто встречающихся случаях решение указанной задачи значительно упрощается.
Случай выпуклости функций fj(x[j]).
В этом случае функции Wj(x[j],x) также являются выпуклыми по x[j] (рис 4.6).
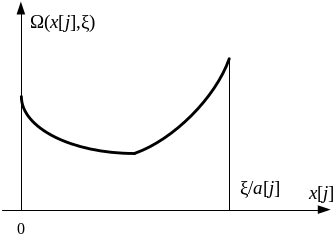 Рис.
4.6.
Рис.
4.6.
Для определения максимума выпуклой функции достаточно сравнить ее значения в крайних точках отрезка [0,x/a[j])] и выбрать наибольшее:
 0,
если
Wj(0,x)³
Wj(x/a[j],x), (4.21)
0,
если
Wj(0,x)³
Wj(x/a[j],x), (4.21)
x[x,j]=
x/a[j], в противном случае.
Случай вогнутости функции fj(x[j]).
В этом случае функции Wj(x[j],x) являются также вогнутыми по x[j]функциями (рис. 4.7).
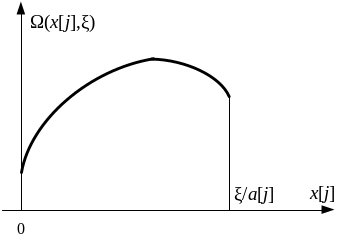
Рис. 4.7.
Для решения одномерной задачи максимизации в этом случае применимы известные методы одномерного поиска экстремума унимодальной функции.
Проблема определения безусловно оптимальных управлений состоит в том, что функции условно оптимальных управлений х[x,j] по x в общем случае являются разрывными (рис.4.8).
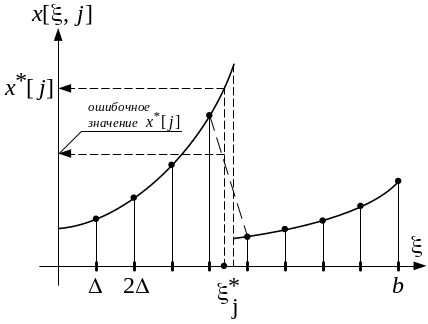
Рис. 4.8.
Если будем табулировать их значения также, как и значения Lj(x), а затем использовать их для определения безусловно оптимальных управлений при обратном ходе по таблице х[x,j], то может возникнуть ситуации, приводящие к значительным ошибкам при определении x*[j]. Это произойдет тогда, когда xj* попадет на место разрыва и использование линейной интерполяции при определении x*[j] по соседним табулированным точкам х[x,j] дает ошибочное значение безусловно оптимального управления, значительно отличающееся от действительного значения.
Выходом из этой проблемы является отказ от табулирования условно оптимальных управлений. Для определения безусловно оптимальных управлений осуществляется повторное решение при обратном ходе оптимизационных задач (4.20) при фиксированных значениях xj*:
![]() W(x[j],xj*). (4.22)
W(x[j],xj*). (4.22)
Все рассмотренные проблемы и подходы к их решению характерны и для других подклассов задач динамического программирования.
