2.5 Проверка прочности, жёсткости и выносливости балки

После подбора сечения балки определяют её фактические геометрические характеристики (моменты инерции, моменты сопротивления и т.п.) и проверяют балку на прочность и жёсткость.

Вычисляем геометрические характеристики сечения подкрановой балки. Момент инерции по формуле, м⁴

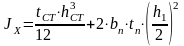
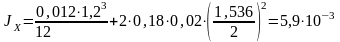
Определяем момент инерции нетто с учетом ослабления верхнего пояса, м⁴

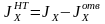
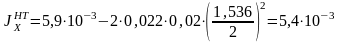
Определяем моменты сопротивления по формулам, м³

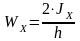
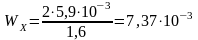
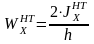
(24)

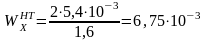
Определим статический момент полусечения по формуле, м³

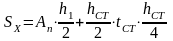
Вычисляем геометрические характеристики тормозной балки относительно вертикальной оси У-У, проходящей через центр тяжести её сечения по формуле, мм

,

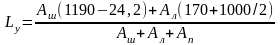где А_ш – площадь сечения швеллера;

А_л – площадь сечения горизонтального листа тормозной балки;

А_п – площадь сечения верхнего пояса подкрановой балки

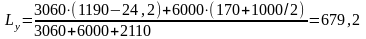
Определяем момент инерции тормозной балки относительно оси У-У по формуле, м⁴

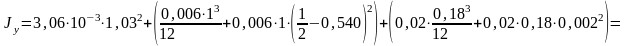
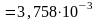
Определяем момент сечения тормозной балки относительно оси У-У по формуле, м³

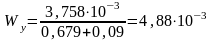
Проверка нормальных напряжений в верхнем поясе подкрановой балки при наличии тормозной балки производится по формуле, МПа

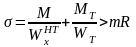
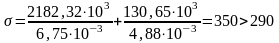
Проверка касательных напряжений на опоре в центре тяжести сечения производится по формуле, МПа

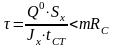
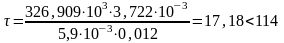
Вычислим сумму моментов инерции сечений верхнего пояса балки и прикреплённого к нему рельса КР-80 по формуле, м⁴

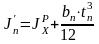
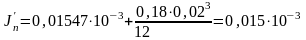
Определяем условную длину распределения нагрузки от колеса крана по формуле, м

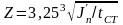
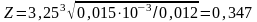
Проверяем прочность стенки балки от действия местных напряжений по формуле, МПа

,

где n₁ – коэффициент, учитывающий неравномерность давления кранового колеса и повышенную динамичность под стыками рельсов;

F_с – расчётная сосредоточенная нагрузка от колеса крана без учёта коэффициента динамичности

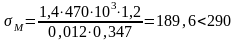
Определяем нормальные напряжения в стенке на уровне поясных швов по формуле, МПа

,

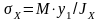где у₁ – расстояние от главной оси х-х до верхней кромки стенки

Определяем среднее касательное напряжение в проверяемом сечении по формуле, МПа

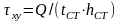
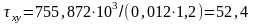
Прочность стенки балки у верхнего пояса по приведенным напряжениям проверяем в сечении, где действует максимальный изгибающий момент по формуле, МПа

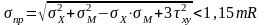
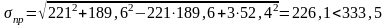
Определим момент от вертикальных нормативных нагрузок, кН∙м

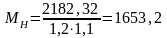
Для проверки жёсткости балки определяем её максимальный прогиб по формуле

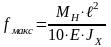
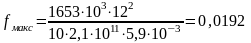
Величина относительного прогиба не должна превышать допустимого, установленного нормами

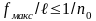
2.6 Проверка общей и местной устойчивости балки

Местная устойчивость сжатого пояса обеспечена при подборе его сечения.

Определяем условную гибкость стенки по формуле

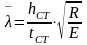
Определяем сечение ребер жёсткости.

Ширина ребра жёсткости определяется по формуле, мм

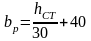
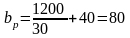
Принимаем b_р=80 мм.

Толщина ребра жёсткости определяется по формуле, мм

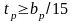
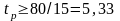
Принимаем t_р=6 мм.

Подкрановая балка имеет постоянное сечение по всей длине.

Поэтому проверку местной устойчивости стенки выполняем для среднего отсека, где наибольшие нормальные напряжения и опорного отсека, где наибольшие касательные напряжения.

Для определения среднего значения изгибающего момента в пределах заданного участка отсека находим значение изгибающего момента в точках 1 и 2 по формулам, кН∙м

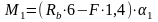
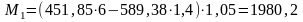
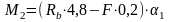
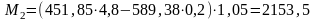
Определяем средний изгибающий момент по формуле, кН∙м

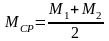
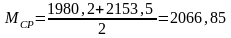
Определяем нормальное напряжение на верхней стенке по формуле, МПа

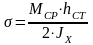
Определяем среднее касательное напряжение по формуле, МПа

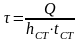
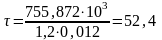
Определяем местное напряжение по формуле, МПа

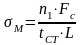
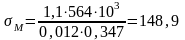
Определяем критические напряжения для среднего отсека.Находим коэффициент γ по формуле

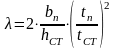
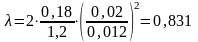
Отношение

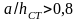
Отношение

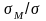
Это отношение не больше предельного, при определённом значении γ=0,831, поэтому нормальное критическое напряжение находим по формуле, МПа

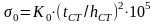
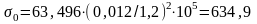
Определяем критическое касательное напряжение по формуле, МПа

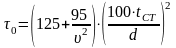
(49)

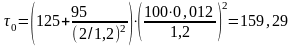
Определяем критическое напряжение от местного давления по формуле, МПа

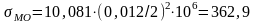
Проверяем устойчивость стенки по формуле

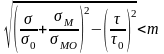
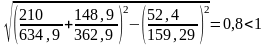
Аналогично производим проверку местной устойчивости стенки для опорного отсека.

Определяем изгибающие моменты в точках 3 и 4 и находим его среднее значение по формулам, кН∙м

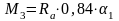
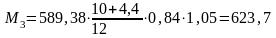
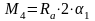
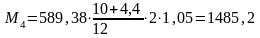
Определяем средний изгибающий момент по формуле, кН∙м

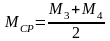
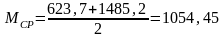
Поперечная сила имеет одинаковое значение по всему отсеку.

Она равна реакции опоры R_а и определяется по формуле

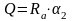
Определяем напряжения в опорном отсеке по формулам, МПа

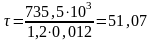
Проверяем устойчивость стенки по формуле

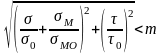
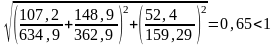
Устойчивость балки в среднем и в опорном отсеках обеспечена.