Варианты контрольных работ для самоконтроля знаний

Контрольная работа

Вариант 1.

1. Из трех орудий произвели залп по цели. Вероятность попадания в цель при одном выстреле из первого орудия равна 0,8; для второго и третьего орудий эти вероятности соответственно равны 0,7 и 0,9. Найти вероятность того, что: а) только один снаряд попадет в цель, б) только два снаряда попадут в цель, в) все три снаряда попадут в цель, г) хотя бы один снаряд попадет в цель.

2. Вероятность появления события в каждом из независимых испытаний равна 0,2. Найти вероятность того, что событие наступит 20 раз в 100 испытаниях.

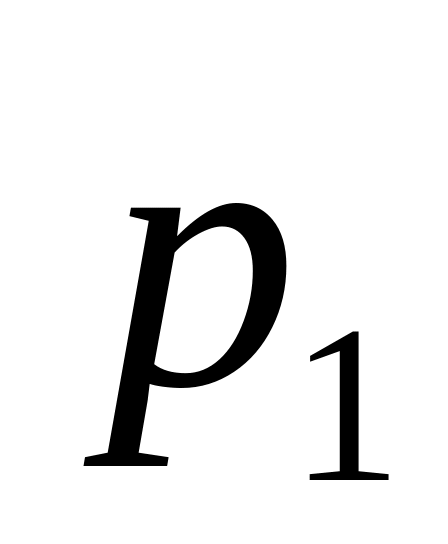3. Найти закон распределения дискретной случайной величины , которая имеет два возможных значения: и , причем . Математическое ожидание , дисперсия и вероятность возможного значения равна 0,9.

4. Случайная величина задана функцией распределения

Требуется: а) найти плотность распределения вероятностей, б) найти математическое ожидание и дисперсию , в) построить графики функции распределения и плотности распределения вероятностей.

5. Найти вероятность попадания в интервал нормально распределенной случайной величины , если известны ее математическое ожидание и среднее квадратическое отклонение .

Вариант 2.

1. Случайная величина задана функцией распределения

Требуется: а) найти плотность распределения вероятностей, б) найти математическое ожидание и дисперсию , в) построить графики функции распределения и плотности распределения вероятностей.

2. Найти вероятность попадания в интервал нормально распределенной случайной величины , если известны ее математическое ожидание и среднее квадратическое отклонение .

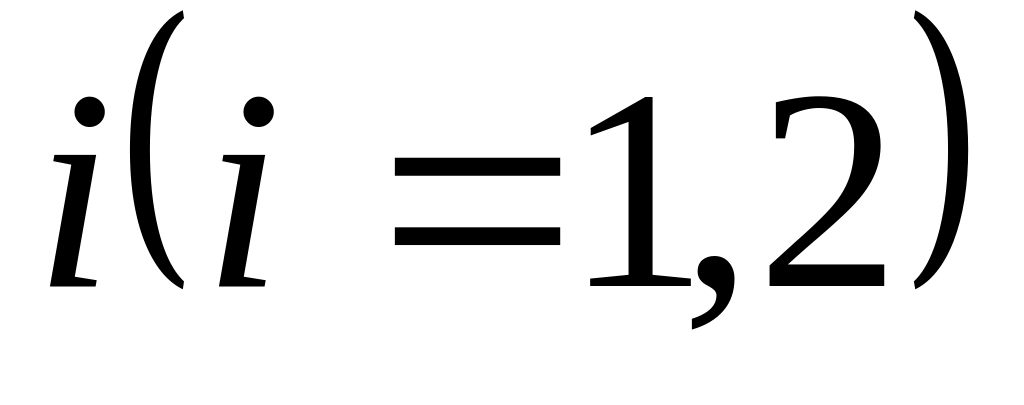3. Задана матрица перехода системы из состояния в состояние за один шаг. Найти матрицу перехода системы из состояния в состояние за два шага.

4. Найти: а) выборочную среднюю, б) выборочную дисперсию, в) выборочное среднее квадратическое отклонение для статистического распределения

	105	100	115	120	125	130	135
	4	6	10	40	20	12	8

5. Найти доверительный интервал для оценки математического ожидания нормального распределения с надежностью 0,95, зная выборочную среднюю , объем выборки и среднее квадратическое отклонение .

Варианты контрольных работ для текущей аттестации

Вариант № 1.

1. Все значения равномерно распределенной случайной величины лежат на отрезке . Найти вероятность попадания случайной величины в промежуток .

2. Случайная величина Х распределена по нормальному закону с математическим ожиданием и дисперсией . Вычислить вероятность попадания случайной величины в интервал .

3. Найти закон распределения дискретной случайной величины Х, которая может принимать только два значения с известной вероятностью и , причем . P₁ =0,1; М(Х)=1,9; D(Х)= 0,09.

4. Найти математическое ожидание, корреляционную функцию и дисперсию случайной величины , где и 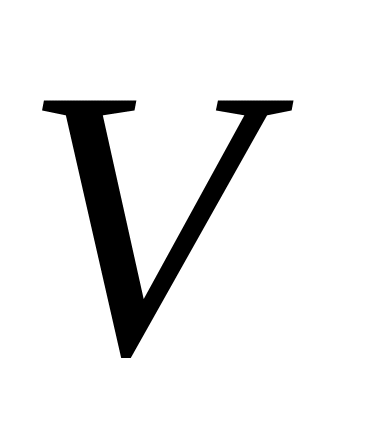- некоррелированные случайные величины, причем М(U)=1, М(V)=2, D(U)=3, D(V)=4.

5. Найти корреляционную функцию стационарной случайной функции Х(t), зная ее спектральную плотность в интервале ; вне этого интервала .

Вариант № 2.

1. Все значения равномерно распределенной случайной величины лежат на отрезке 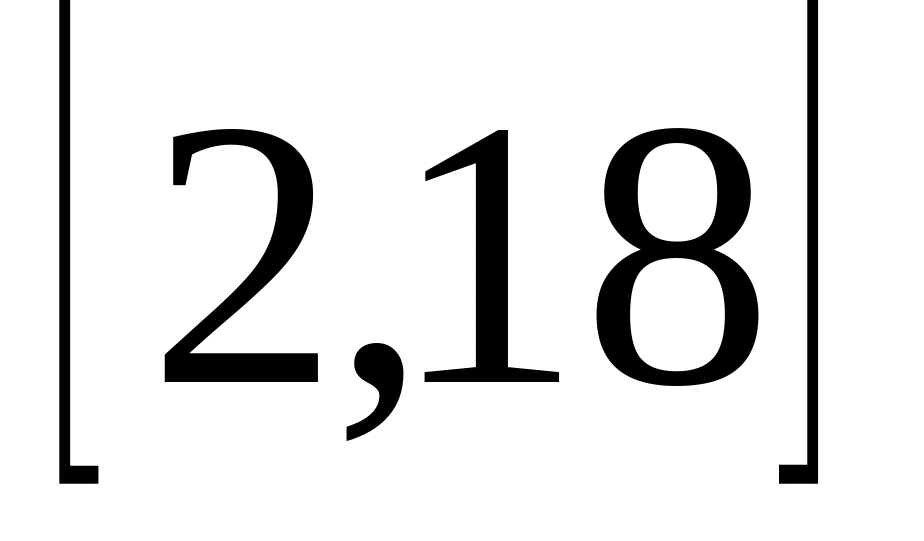. Найти вероятность попадания случайной величины в промежуток .

2. Случайная величина Х распределена по нормальному закону с математическим ожиданием и дисперсией . Вычислить вероятность попадания случайной величины в интервал .

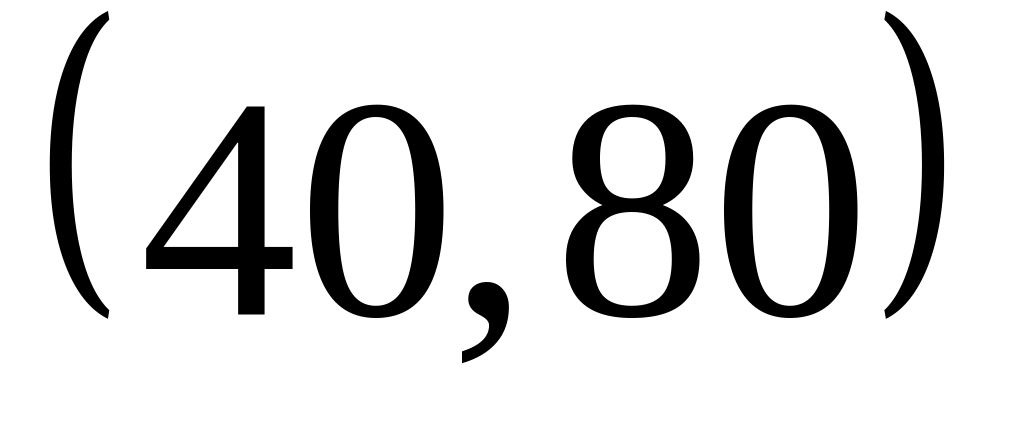3. Найти закон распределения дискретной случайной величины Х, которая может принимать только два значения с известной вероятностью и , причем . P₁ = 0,2; М(Х)=2,6; D(Х)= 0,64.

4. Найти математическое ожидание, корреляционную функцию и дисперсию случайной величины , где и - некоррелированные случайные величины, причем М(U)=2, М(V)=3, D(U)=4, D(V)=4.

5. Найти корреляционную функцию стационарной случайной функции Х(t), зная ее спектральную плотность в интервале 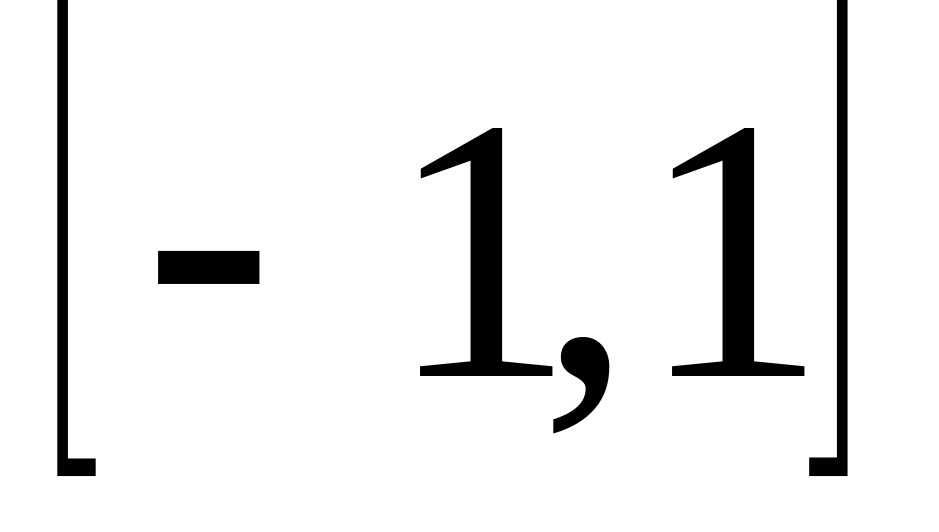; вне этого интервала .

Вариант № 3.

1. Все значения равномерно распределенной случайной величины лежат на отрезке 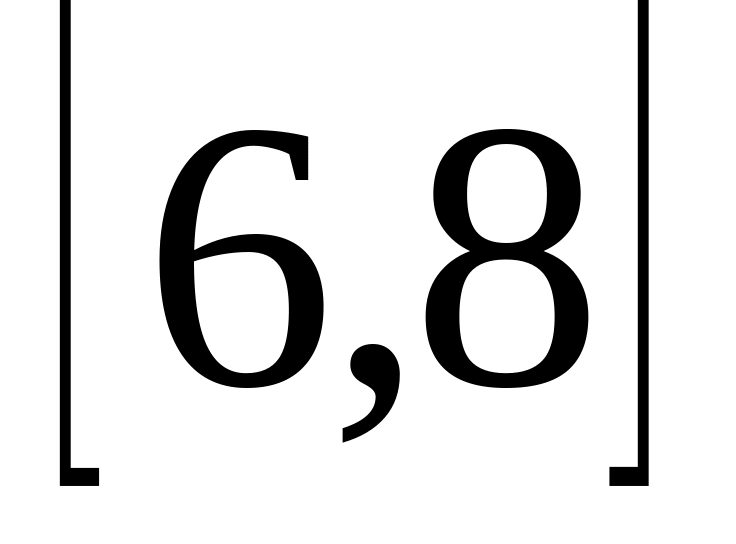. Найти вероятность попадания случайной величины в промежуток .

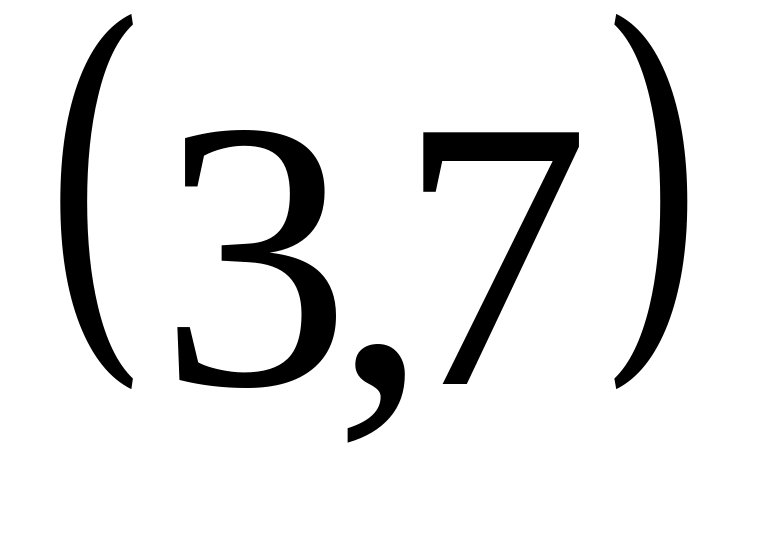2. Случайная величина Х распределена по нормальному закону с математическим ожиданием 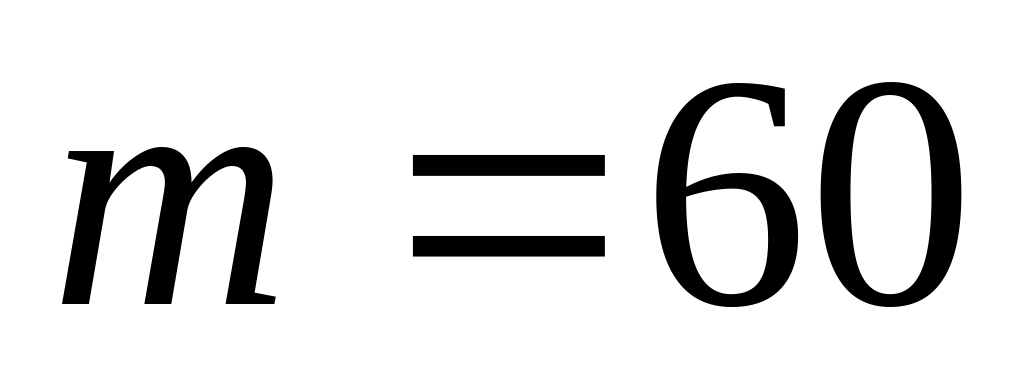и дисперсией . Вычислить вероятность попадания случайной величины в интервал .

3. Найти закон распределения дискретной случайной величины Х, которая может принимать только два значения с известной вероятностью и , причем . P₁ =0,3; М(Х)=3,1; D(Х)= 1,89.

4. Найти математическое ожидание, корреляционную функцию и дисперсию случайной величины , где и - некоррелированные случайные величины, причем М(U)=4, М(V)=5, D(U)=1, D(V)=3.

5. Найти корреляционную функцию стационарной случайной функции Х(t), зная ее спектральную плотность в интервале ; вне этого интервала .