МИНОБРНАУКИ РФ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Южно-Российский государственный университет экономики и сервиса»

(ФГБОУ ВПО «ЮРГУЭС»)

УТВЕРЖДАЮ

Заведующий кафедрой «Математика»

_______________ И.М.Мальцев

28 августа 2012 г.

КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫ (КИМ)

ДЛЯ ВСЕХ ВИДОВ КОНТРОЛЯ

ПО ДИСЦИПЛИНЕ

«МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»

для направления 030300 Психология

Составитель:

К.с.н., доцент Ю.А. Хоменко

Шахты - 2012

Вопросы для промежуточной аттестации к контрольным точкам по дисциплине «Математическая статистика»

Первая контрольная точка

1. Дайте классическое определение вероятности. В чем состоит различие между вероятностью и относительной частотой?

2. Дайте определение суммы событий. Докажите теорему сложения.

3. Дайте определение произведения событий. Докажите теорему умножения.

4. Докажите формулу Бернулли.

5. Докажите формулу полной вероятности.

6. Докажите формулы Бейеса.

7. Дайте определение математического ожидания и докажите его свойства.

8. Дайте определение дисперсии и докажите ее свойства.

9. Дайте определение среднего квадратического отклонения и докажите его преимущества по сравнению с дисперсией.

10. Дайте определение функции распределения и докажите ее свойства.

11. Дайте определение плотности распределения вероятности и докажите ее свойства.

12. Напишите формулы плотности нормального и показательного распределений. Какими параметрами определяются эти распределения?

13. Как найти вероятность попадания случайной величины в заданный интервал, если она распределена: а) нормально, б) показательному закону.

14. Дайте определение функции распределения и плотности распределения вероятностей двумерной непрерывной случайной величины.

15. Как найти вероятность попадания случайной величины в заданную область?

16. Дайте определение случайной функции, сечения и реализации.

17. Дайте определения математического ожидания и дисперсии случайной функции и докажите их свойства.

18. Дайте определение корреляционной функции и перечислите ее свойства.

19. Как, зная корреляционную функцию случайной функции, найти ее дисперсию?

Вторая контрольная точка

20. Сформулируйте и докажите теоремы о характеристиках производной от случайной функции.

21. Сформулируйте и докажите теоремы о характеристиках интеграла от случайной функции.

22. Дайте определение стационарной случайной функции.

23. Сформулируйте и докажите свойства корреляционной функции и от стационарной случайной функции.

24. Напишите формулы для вычисления выборочной средней и выборочной дисперсии.

25. Как построить гистограмму?

26. Дайте определение несмещенной, эффективной и состоятельной оценок.

27. Является ли выборочная дисперсия несмещенной оценкой генеральной дисперсии? Что такое исправленная дисперсия?

28. Для чего служит метод наибольшего правдоподобия? Как им пользоваться для дискретных и непрерывных случайных величин?

29. Как найти доверительные интервалы для оценки математического ожидания нормального распределения?

30. Как найти доверительные интервалы для оценки среднего квадратического отклонения нормально распределенной случайной величины?

31. Какую зависимость называют корреляционной?

32. Какую корреляцию называют линейной?

33. Перечислите свойства выборочного коэффициента корреляции. Как найти этот коэффициент?

34. Напишите выборочное уравнение прямой линии регрессии на .

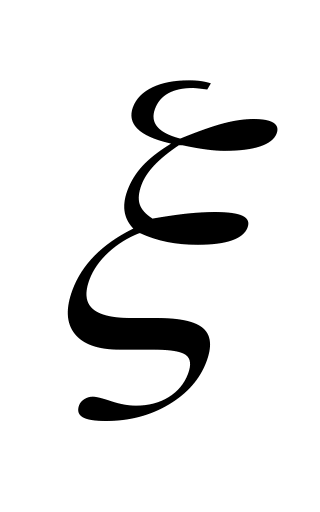35. Дайте определение статистической гипотезы.

36. Что называют ошибкой первого (второго) рода?

37. Что такое уровень значимости? Приведите значения уровней значимости, наиболее употребительных на практике.

38. Проверка гипотезы о нормальном распределении генеральной совокупности по критерию Пирсона.

39. Моделирование дискретной случайной величины методом Монте-Карло.

40. Моделирование непрерывной случайной величины методом Монте-Карло.

Варианты контрольных работ для промежуточной аттестации

Вариант № 1.

1. Ящик содержит 90 годных и 10 бракованных деталей. Найти вероятность того, что среди 10 вынутых из ящика деталей нет бракованных.

2. На фабрике, изготовляющей, болты, первая машина производит 25%, вторая – 35%, третья – 40% всех изделий. Брак в их продукции составляет соответственно 5%, 4%, 2%. Какова вероятность того, что случайно выбранный болт оказался дефектным?

3. Вероятность попадания в цель при каждом выстреле равна 0,001. Найти вероятность попадания в цель двумя и более выстрелами при залпе в 5000 выстрелов.

4. Стрелок производит по мишени три выстрела. Вероятность попадания в мишень при каждом выстреле равна 0,3. Построить ряд распределения числа попаданий.

5. Случайная величина Х характеризуется рядом распределения

Х	0	1	2	3	4
р	0,2	0,4	0,3	0,08	0,02

Определить математическое ожидание и дисперсию.

Вариант № 2.

1. Ящик содержит 80 годных и 10 бракованных деталей. Найти вероятность того, что среди 5 вынутых из ящика деталей нет бракованных.

2. На фабрике, изготовляющей, болты, первая машина производит 25%, вторая – 35%, третья – 40% всех изделий. Брак в их продукции составляет соответственно 5%, 6%, 8%. Какова вероятность того, что случайно выбранный болт оказался дефектным?

3. Вероятность попадания в цель при каждом выстреле равна 0,002. Найти вероятность попадания в цель двумя и более выстрелами при залпе в 1000 выстрелов.

4. Стрелок производит по мишени три выстрела. Вероятность попадания в мишень при каждом выстреле равна 0,2. Построить ряд распределения числа попаданий.

5. Случайная величина Х характеризуется рядом распределения

Х	3	4	5	6	7
р	0,2	0,4	0,3	0,08	0,02

Определить математическое ожидание и дисперсию.

Вариант № 1.

6. Ящик содержит 90 годных и 10 бракованных деталей. Найти вероятность того, что среди 10 вынутых из ящика деталей нет бракованных.

7. На фабрике, изготовляющей, болты, первая машина производит 25%, вторая – 35%, третья – 40% всех изделий. Брак в их продукции составляет соответственно 5%, 4%, 2%. Какова вероятность того, что случайно выбранный болт оказался дефектным?

8. Вероятность попадания в цель при каждом выстреле равна 0,001. Найти вероятность попадания в цель двумя и более выстрелами при залпе в 5000 выстрелов.

9. Стрелок производит по мишени три выстрела. Вероятность попадания в мишень при каждом выстреле равна 0,3. Построить ряд распределения числа попаданий.

10. Случайная величина Х характеризуется рядом распределения

Х	0	1	2	3	4
р	0,2	0,4	0,3	0,08	0,02

Определить математическое ожидание и дисперсию.

Вариант № 2.

6. Ящик содержит 80 годных и 10 бракованных деталей. Найти вероятность того, что среди 5 вынутых из ящика деталей нет бракованных.

7. На фабрике, изготовляющей, болты, первая машина производит 25%, вторая – 35%, третья – 40% всех изделий. Брак в их продукции составляет соответственно 5%, 6%, 8%. Какова вероятность того, что случайно выбранный болт оказался дефектным?

8. Вероятность попадания в цель при каждом выстреле равна 0,002. Найти вероятность попадания в цель двумя и более выстрелами при залпе в 1000 выстрелов.

9. Стрелок производит по мишени три выстрела. Вероятность попадания в мишень при каждом выстреле равна 0,2. Построить ряд распределения числа попаданий.

10. Случайная величина Х характеризуется рядом распределения

Х	3	4	5	6	7
р	0,2	0,4	0,3	0,08	0,02

Определить математическое ожидание и дисперсию.

Вариант № 3.

1. Ящик содержит 70 годных и 7 бракованных деталей. Найти вероятность того, что среди 7 вынутых из ящика деталей нет бракованных.

2. На фабрике, изготовляющей, болты, первая машина производит 25%, вторая – 35%, третья – 40% всех изделий. Брак в их продукции составляет соответственно 3%, 5%, 2%. Какова вероятность того, что случайно выбранный болт оказался дефектным?

3. Вероятность попадания в цель при каждом выстреле равна 0,003. Найти вероятность попадания в цель двумя и более выстрелами при залпе в 6000 выстрелов.

4. Стрелок производит по мишени три выстрела. Вероятность попадания в мишень при каждом выстреле равна 0,4. Построить ряд распределения числа попаданий.

5. Случайная величина Х характеризуется рядом распределения

Х	2	5	6	7	7
р	0,2	0,4	0,3	0,08	0,02

Определить математическое ожидание и дисперсию.

Вариант № 4.

1. Ящик содержит 70 годных и 7 бракованных деталей. Найти вероятность того, что среди 7 вынутых из ящика деталей нет бракованных.

2. На фабрике, изготовляющей, болты, первая машина производит 25%, вторая – 35%, третья – 40% всех изделий. Брак в их продукции составляет соответственно 3%, 5%, 2%. Какова вероятность того, что случайно выбранный болт оказался дефектным?

3. Вероятность попадания в цель при каждом выстреле равна 0,003. Найти вероятность попадания в цель двумя и более выстрелами при залпе в 6000 выстрелов.

4. Стрелок производит по мишени три выстрела. Вероятность попадания в мишень при каждом выстреле равна 0,4. Построить ряд распределения числа попаданий.

5. Случайная величина Х характеризуется рядом распределения

Х	2	5	6	7	7
р	0,2	0,4	0,3	0,08	0,02

Определить математическое ожидание и дисперсию.