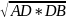Площадь.

1.Равные многоугольники имеют равные S.

2.S квадрата равна квадрату его стороны.

3. Если многоугольник составлен из нескольких многоугольников, то его S = сумме площадей этих многоугольников.

Теорема: S прямоугольника равен произведению его смежных сторон.

S = a * b

Теорема: S параллелограмма равен произведению его основания на высоту.

S = AD *BH

Теорема: S треугольника равен произведению его основание на высоту.

S = ½ АВ*СН

S прямоугольного треугольника = 1/2

произведения его катетов.

Формула Герона:

,

где р =1/2 (а + b + c)- полупериметр треугольника.

Теорема: S трапеции = про- изведению полу суммы её оснований на высоту.

Теорема: (Пифагора) В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

c²=a² + b²

Теорема: Если квадрат 1ой

стороны треугольника = сумме

квадратов 2 других сторон, то

треугольник прямоугольный.

Определение: два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорционально сходственны сторонам другого.

АВ и А₁В₁, ВС и В₁С₁ , СА и С₁А₁ – сходственные стороны

Теорема: Отношение S 2ух подобных треугольников равен квадрату коэффициента подобия.

Признаки подобия треугольников

Первый признак

Теорема: Если два угла одного треугольника соответственно равны двум углам другого, то такие 3-угольники подобны.

Второй признак

Теорема: Если две стороны одного треугольника пропорциональны двум

сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны.

Третий признак

Теорема: Если три стороны одного треугольника пропорциональ-ны трём сторонам другого, то такие треугольники подобны.

Теорема: Средняя линия параллельна одной из его сторон и равна ½ этой стороны.

MN = ½ AC

Утверждение: Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которое делится гипотенуза этой высотой.

CD =

Утверждение: Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла.

AC =

Соотношения между сторонами и углами прямоугольного треугольника

sin острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

sin A =

cos острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

cos A =

tg острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

tg A =

tg угла = отношению sin к cos

этого угла: tg = sin/ cos.

Основное тригонометрическое тождество:

sin²α + cos²α=1.