
Двойственность кванторов.
![]()
Не для всех x
![]() истина. Значит, что существует x,
где
истина. Значит, что существует x,
где
![]() ложь, а не истина.
ложь, а не истина.
![]()
Не существует x,
где
![]() истина. Значит, для всех x
истина. Значит, для всех x
![]() ложь, а не истина.
ложь, а не истина.
Определение формулы.
Определение 4.
Термом
будем называть любую предметную
переменную или константу. Под термом
будем понимать функциональную букву
![]() – терм.
– терм.
Определение 5.
Атомарной формулой
(атомом)
будем называть любое переменное
высказывание (из числа логических
высказываний) или предикат. Предикат
![]() – атомарная формула.
– атомарная формула.
Определение 5.
Любой атом – формула.
Если A
и
B
– формулы, то
![]() тоже формулы.
тоже формулы.
Других формул нет.
Таким образом, вся логика высказываний входит в логику предикатов. Логика предикатов занимается теорией вывода.
Определение 6.
Интерпретацией будем называть систему, состоящую из непустого множества D, называемого областью интерпретации (универсумом), и некоторого соответствия предметной букве.
![]() n-местное
отношение, т. е.
n-местное
отношение, т. е.
![]() .
.
Каждой n-местную
функцию, т. е.
![]() .
.
Каждой константе
любой предикат из D
![]() .
.
Замечание.
В данной интерпретации любая формула без свободных переменных есть высказывание. А любая формула со свободными переменными – отношение, которое может быть или истинным или ложным.
Лекция № 3. Булевы функции (фал).
Три типа формул:
-
Общезначимая ППФ – истинна при любой интерпретации.
-
Противоречивая ППФ – ложна при любой интерпретации.
-
Остальные (выполнимые) истинны хотя бы при одной интерпретации.
Пример.
-
╞

«Из общего следует частное».
Докажем от противного.
Имеем область интерпретации D, где принимает значение «ложь».
╞![]() – ложь.
– ложь.
Для всех x
![]() истинна, но
истинна, но
![]() ,
где
,
где
![]() – ложь.
– ложь.
![]() D
быть не может.
D
быть не может.
-
╞

«Из частного следует тоже частное».
Докажем от противного.
Имеем область интерпретации D, где принимает значение «ложь».
╞![]() – ложь.
– ложь.
Возможно только,
если x
= y.
![]() Противоречие.
Противоречие.
Теорема 1.
а) ╞![]()
б) ╞![]()
Вычисление
значений формул
![]() для данного присвоения значений
переменных состоит из вычислений
значений логической функцией, поставленной
в соответствие этой A,
а значение всей формулы совпадает с
вычислениями из примеров 1 и 2.
для данного присвоения значений
переменных состоит из вычислений
значений логической функцией, поставленной
в соответствие этой A,
а значение всей формулы совпадает с
вычислениями из примеров 1 и 2.
Следствие.
╞![]() ,
то ╞
,
то ╞![]() .
.
╞
![]()
(из частного не следует общее).

Теорема 2.
Пусть x – некоторая предметная переменная и B – формула, не имеющая свободного вхождения x. A(x) – формула.
а) ╞![]() ,
то ╞
,
то ╞![]()
б) ╞![]() ,
то ╞
,
то ╞![]()
а) Пусть для
некоторой D,
где B
принимает значение ложь. По определению
импликации (понятно). Пусть имеется D,
где B
принимает значение истины. А если A(x)
истина, то тоже истина
![]() .
.
б) Доказывается аналогично.
Следствие.
╞![]() ,
то ╞
,
то ╞![]()
-
╞
 1
аксиома
1
аксиома -
╞

-
╞
 MP(1,2)
MP(1,2)
Применяя теорему 2а можем на А(x) навесить квантор общности.
-
╞

-
╞
 ,
где ╞
,
где ╞
-
╞
 MP(4,5)
MP(4,5)
Логика предикатов как формальная система.
Термы.
![]() – счётное множество
предметных переменных.
– счётное множество
предметных переменных.
![]() – непустое конечное
или счётное множество предметных
символов.
– непустое конечное
или счётное множество предметных
символов.
![]() – пустое, конечное
или счётное множество функциональных
символов
– пустое, конечное
или счётное множество функциональных
символов
![]() – пустое, конечное
или счётное множество предметных
констант.
– пустое, конечное
или счётное множество предметных
констант.
Логические связки:
![]()
Кванторы:
![]()
Вспомогательные
символы:
![]()
Других термов нет.
Правила построения ППФ.
![]()
-
Любая атомарная ППФ – суть атом (атомарная формула) ППФ, переменная логики высказывания или предикат.
-
Если А и B – ППФ и x – предметная переменная, то

 – ППФ.
– ППФ. -
Других правил нет.
Система аксиом.
11 аксиом.
12.
![]()
13.
![]()
![]()
-
Все аксиомы суть теоремы (выводимы).
-
Правило подстановки, но имеем дело с такой подстановкой термов
 вместо
вместо
 в формулу A.
После подстановки
в формулу A.
После подстановки
 будет свободна для этих термов.
будет свободна для этих термов. -
Правило обобщения (Gen). Если выводимо ├
 ,
где B
не имеет свободного вхождения x,
то ├
,
где B
не имеет свободного вхождения x,
то ├ .
. -
Правило конкретизации (Ex). Если выводимо ├
 ,
где B
не имеет свободного вхождения x,
то ├
,
где B
не имеет свободного вхождения x,
то ├ .
. -
Modus ponens (MP).
-
Если A – теорема, имеющая квантор
 или
или
 ,
то теоремой будет A’,
полученная из A
путём замены одной связанной переменной
буквами отличными от букв связанных
переменных.
,
то теоремой будет A’,
полученная из A
путём замены одной связанной переменной
буквами отличными от букв связанных
переменных. -
Других нет.
Будем считать, что
некоторая ППФ
![]() ├
├![]() (далее для краткости
(далее для краткости
![]() ├
├![]() ).
).
-
 ├
├
-
├
 ,
то
,
то
 ├
├
-
 ├
├ и
и
 ├
├ ,
то
,
то
 ├
├
-
 ├
├ ,
если
,
если
 и
и
 не имеют свободного вхождения x,
то
не имеют свободного вхождения x,
то
 ├
├
-
 ├
├ ,
то
,
то
 ├
├
-
 ├
├ ,
то
,
то
 ├
├ ,
,
 получено из B
путём подстановки вместо свободных
вхождений в B
переменных.
получено из B
путём подстановки вместо свободных
вхождений в B
переменных. -
 ├
├ ,
то
,
то
 ├
├ ,
,
 получено из B
переименованием связанных переменных.
получено из B
переименованием связанных переменных.
Теорема Дедукции.
Если
![]() ├
├![]() ,
то ├
,
то ├![]() ,
,
![]() ├
├![]()
-
├
 9
аксиома
9
аксиома -
├
 подстановка
подстановка -
 ├
├ MP
MP -
 ├
├ т.
дедукции
т.
дедукции -
├
 т.
дедукции
т.
дедукции -
├
 силлогизм(2,5)
силлогизм(2,5)
Правило соединения посылок:
![]() ├
├![]()
├![]()
-
 ├
├
-
├
 3
аксиома
3
аксиома -
├

-
 ├
├ MP(1,2)
MP(1,2) -
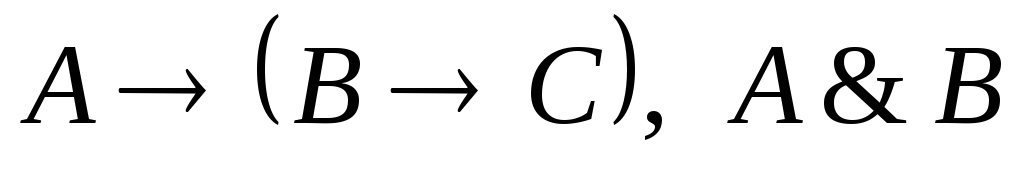 ├
├ условие
1
условие
1 -
 ├
├ MP(4,5)
MP(4,5) -
 ├
├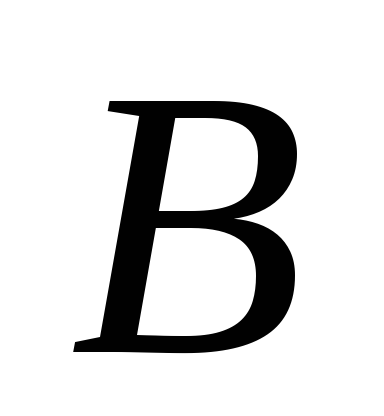 MP(1,3)
MP(1,3) -
 ├
├ MP(6,7)
MP(6,7) -
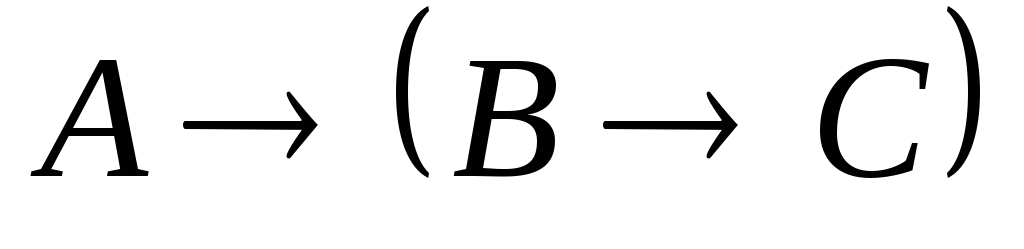 ├
├
├![]()
-
├
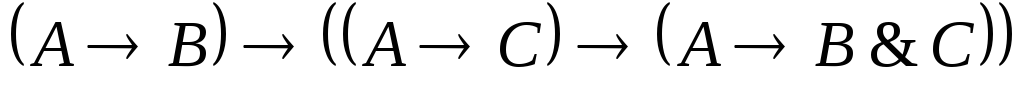 5
аксиома
5
аксиома -
├
 подстановка
подстановка -
├

-
├
 MP(2,3)
MP(2,3) -
├
 подстановка
подстановка -
├

-
├
 силлогизм(5,6)
силлогизм(5,6) -
├
 подстановка
подстановка -
├
 следствие
теоремы дедукции
следствие
теоремы дедукции
(правило перестановки мест посылок)
|
|
