
МОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ
(ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)
Лекции
Дискретная математика
5 Семестр
Лектор Вагин Вадим Николаевич
Москва, 2010/2011
Лекция № 1. Булевы функции (фал).
2. Правило перестановки мест посылок.
![]() ├
├![]()
-
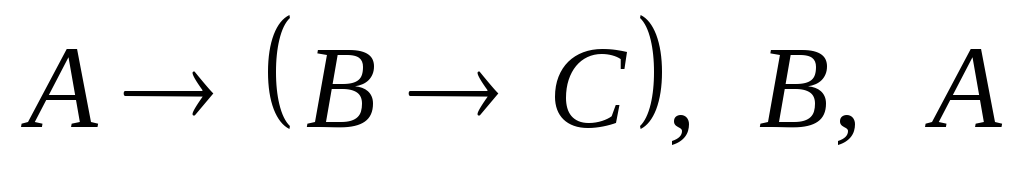 ├
├ условие
выводимости 1
условие
выводимости 1 -
├ Условие выводимости 1
-
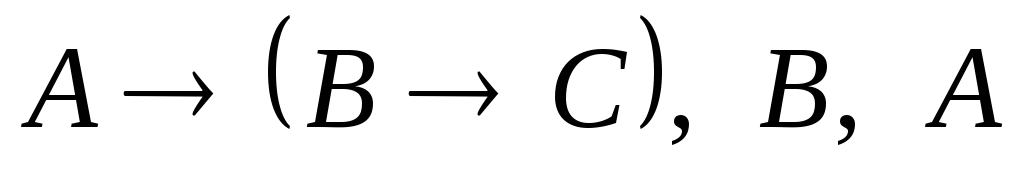 ├
├ MP(1,2)
MP(1,2) -
├ Условие выводимости 1
-
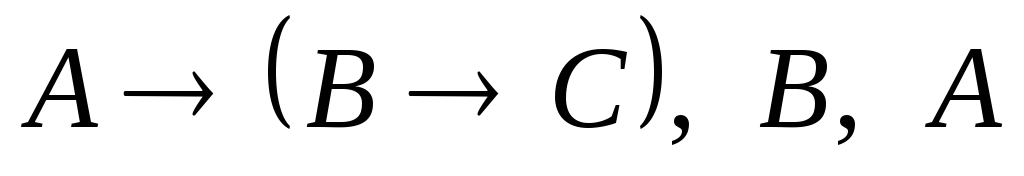 ├
├ MP(3,4)
MP(3,4) -
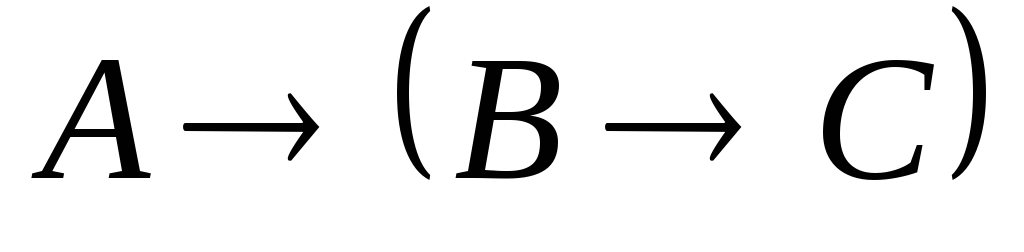 ├
├ теорема
дедукции
теорема
дедукции -
├ Теорема дедукции
3. Правило объединения посылок.
![]() ├
├![]()
4. Правило разъединения посылок.
![]() ├
├![]()
Свойства системы аксиом:
-
Непротиворечивость.
-
Полнота.
-
Независимость.
╞ Общезначимость (знак тождественной истинности).
Теорема 1.
Теорема состоятельности.
Любая выводимая ППФ (теорема) общезначима.
Все аксиомы – суть общезначимые ППФ. Правила вывода устроены так, что из общезначимых ППФ получаем всегда общезначимые. Таким образом, все теоремы – общезначимые ППФ.
Лемма 1.
Пусть A
– ППФ и
![]() – буквы, в неё входящие. Пусть дано
некоторое распределение истинностных
значений всех букв
– буквы, в неё входящие. Пусть дано
некоторое распределение истинностных
значений всех букв
![]() в ППФ A.
Пусть
в ППФ A.
Пусть
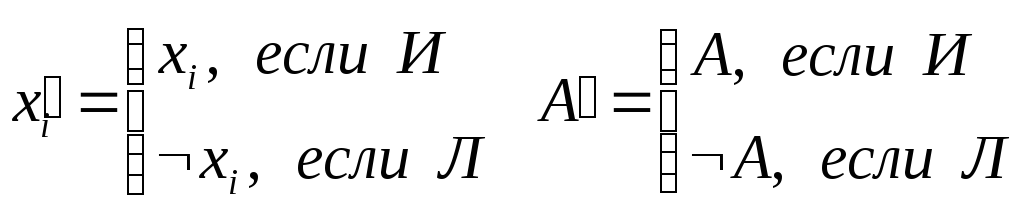
Тогда из
![]() ├
├![]() .
.
Докажем методом математической индукции по числу логических связок в ППФ А.
-
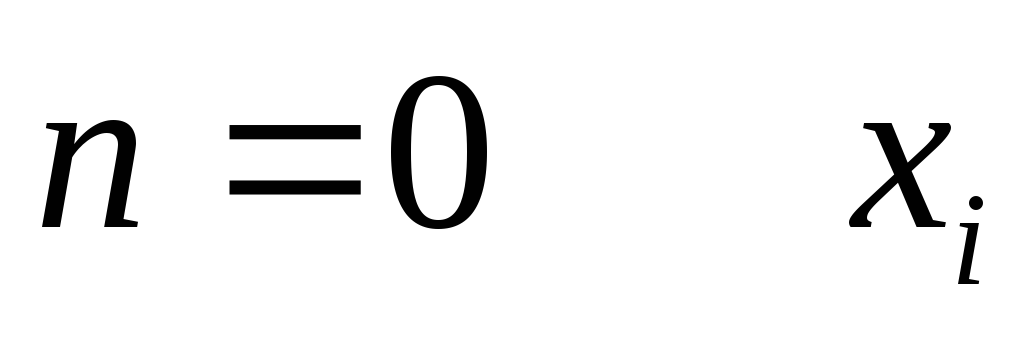 ├
├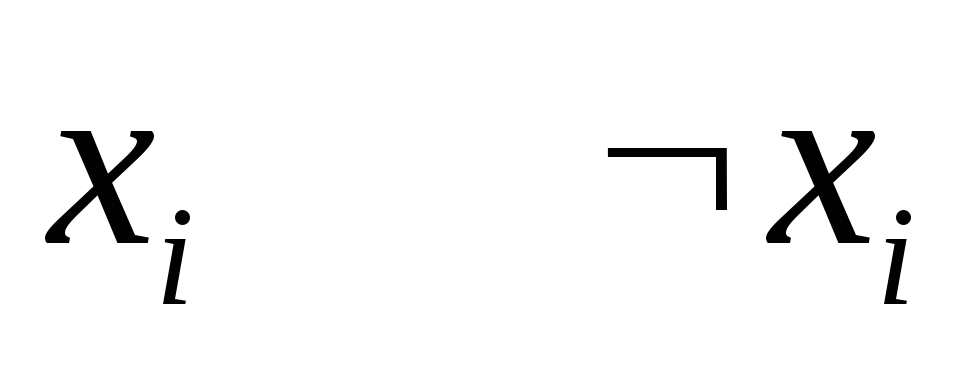 ├
├
-
Пусть лемма верна при числе логических связок
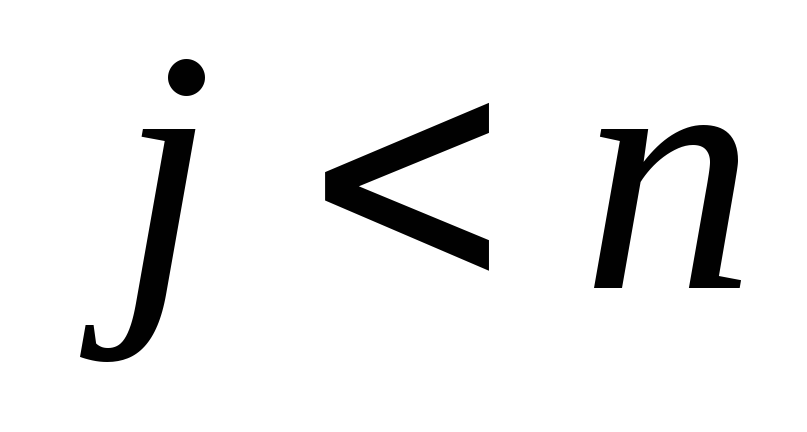 .
.
Докажем, что она
верна и при
![]() .
.
-
Пусть А есть
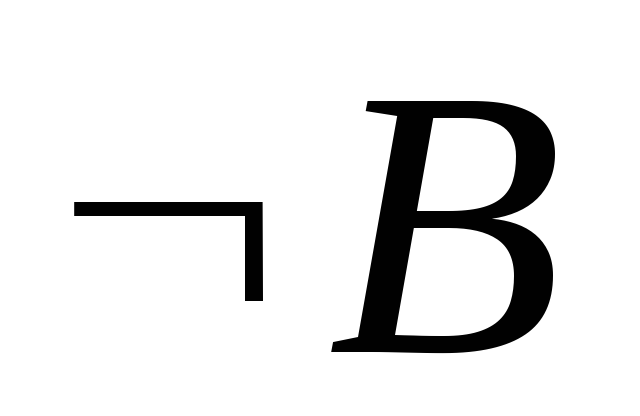 .
.-
Пусть B – истина, тогда
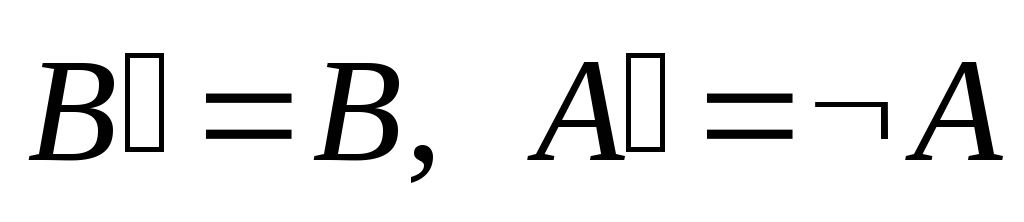 .
.
-
По индуктивному предположению:
![]() ├
├![]()
![]() ├
├![]() 10
аксиома
10
аксиома
![]() ├
├![]() МР
МР
![]() ├
├![]()
-
Пусть B – ложь, тогда
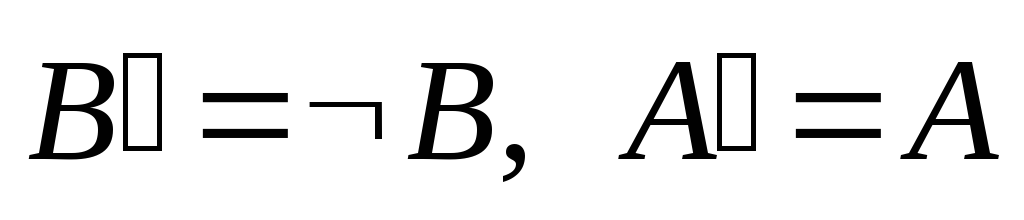 .
.
По индуктивному предположению:
![]() ├
├![]()
![]() ├
├![]()
-
Пусть А имеет вид
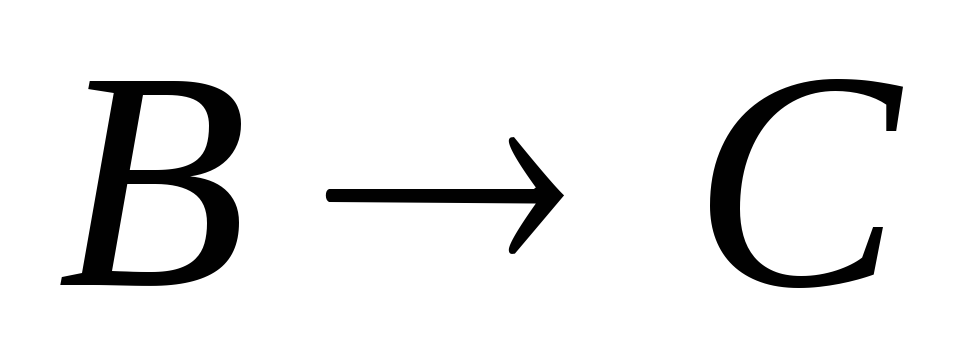 .
.-
Пусть A – истина, тогда
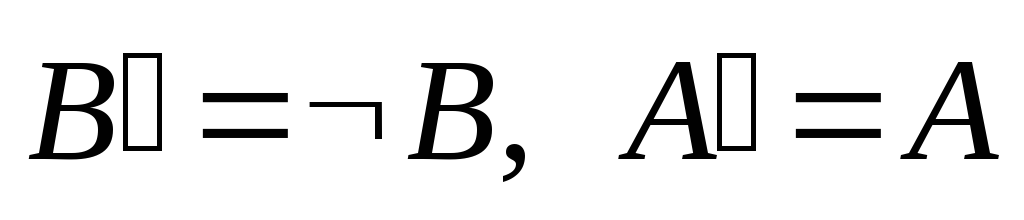 .
.
-
По индуктивному предположению:
![]() ├
├![]()
![]() ├
├![]()
![]() ├
├![]() МР
МР
![]() ├
├![]()
-
Пусть
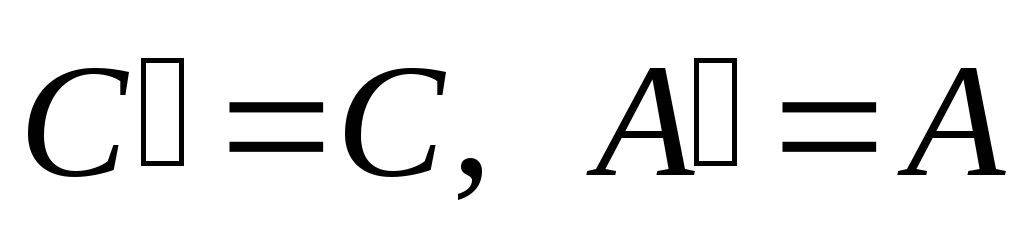 .
.
По индуктивному предположению:
![]() ├
├![]()
![]() ├
├![]() 1
аксиома
1
аксиома
![]() ├
├![]() МР
МР
![]() ├
├![]()
-
Пусть B – истина, C – ложь, тогда
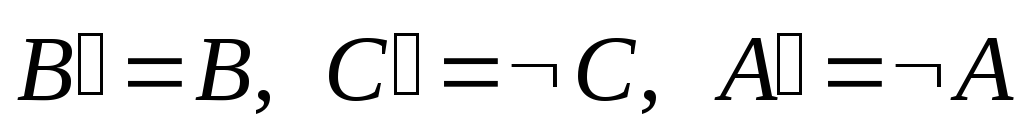 .
.
По индуктивному предположению:
![]() ├
├![]()
![]() ├
├![]()
![]() ├
├![]() теорема
дедукции
теорема
дедукции
![]() ├
├![]() 2xMP
2xMP
![]() ├
├![]()
Теорема 2.
Теорема о полноте (в широком смысле).
Любая общезначимая ППФ является теоремой (выводима).
Предположим,
что А – суть общезначимая ППФ и
![]() в неё входят. Тогда по лемме 1
в неё входят. Тогда по лемме 1
![]() ├
├![]() .
.
-
Пусть
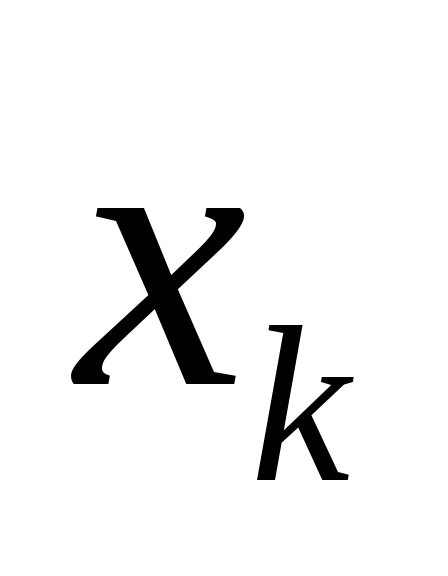 – истина, тогда
– истина, тогда
 ├
├ ;
;
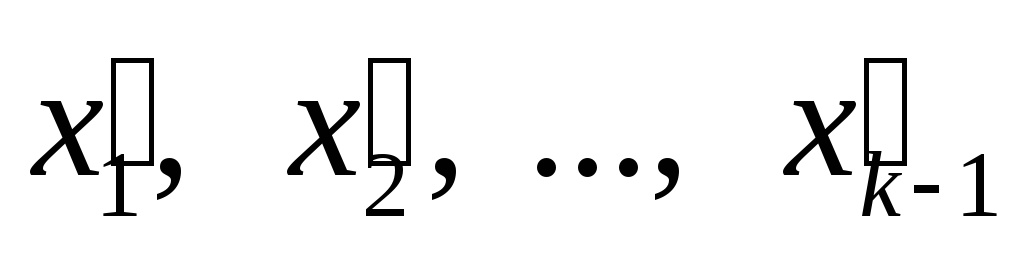 ├
├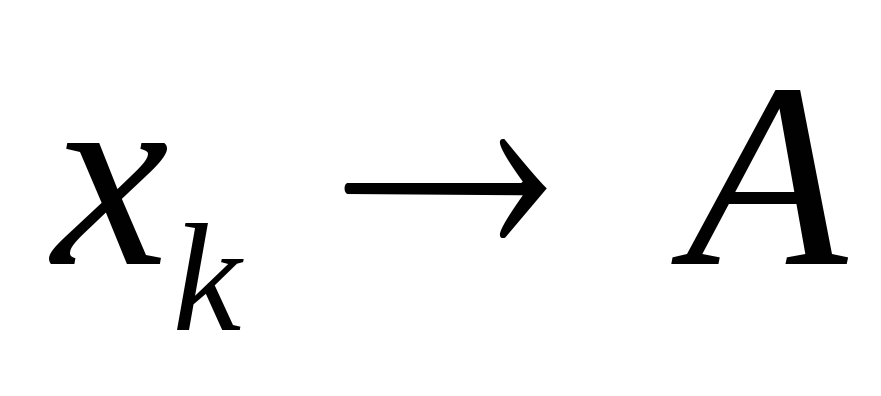 .
. -
Пусть
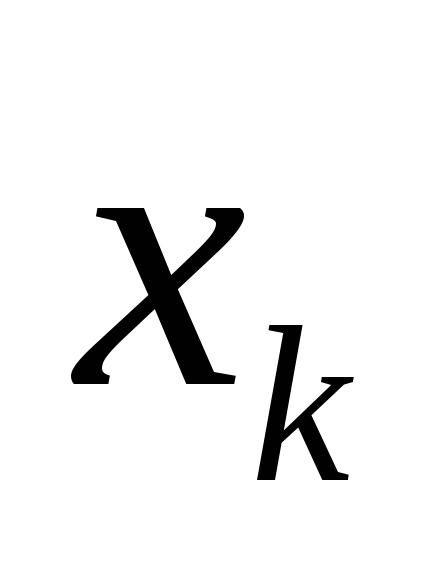 – ложь, тогда
– ложь, тогда
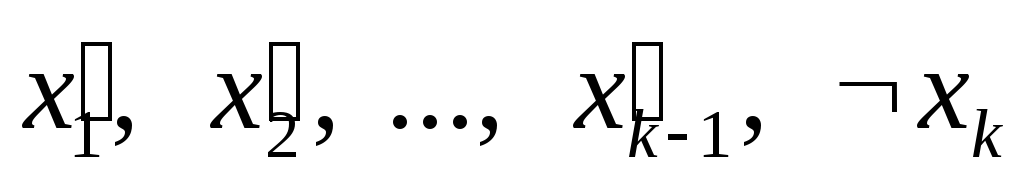 ├
├ ;
;
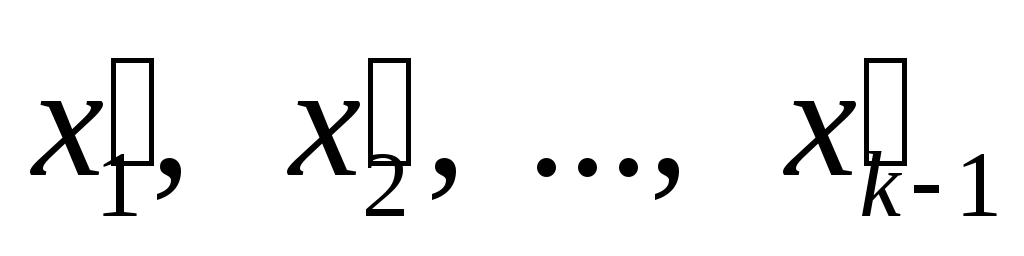 ├
├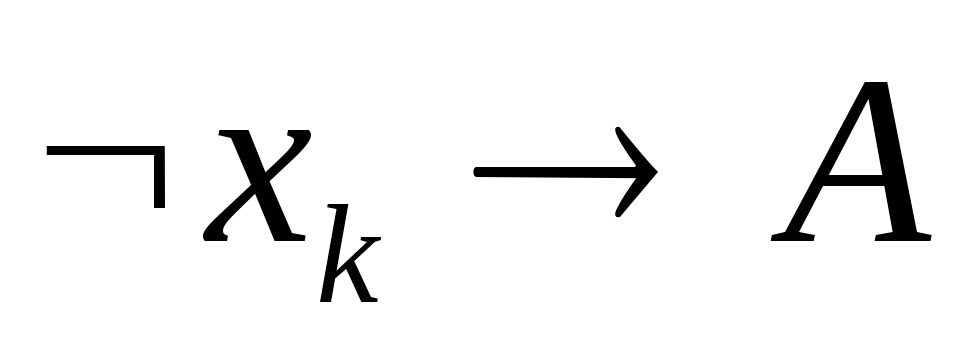 .
.
![]() ├
├![]()
![]() ├
├![]() MP
MP
Повторяем k – 1 раз. Получаем А как ППФ.
Замечание.
Кроме понятия полноты в широком смысле существует понятие полноты в узком смысле.
Теорема 3.
О непротиворечивости.
Логическое
высказывание непротиворечиво, т. е.
нельзя одновременно вывести и
![]() и
и
![]() .
.
Определение 1.
Аксиома независима, если она не выводима из остальных аксиом формальных систем.
Определение 2.
Система аксиом независима, если любая аксиома этой системы независима, т. е. не выводима из остальных.
Лекция № 2.
 БУЛЕВЫ
ФУНКЦИИ (ФАЛ).
БУЛЕВЫ
ФУНКЦИИ (ФАЛ).
├![]()
Считаем, что все логические связки имеют стандартную истинностную таблицу.
Утверждение
![]() есть
есть
![]() .
.
Тогда первые 8 аксиом остаются общезначимыми. Проверим 9, 10 и 11 аксиомы.
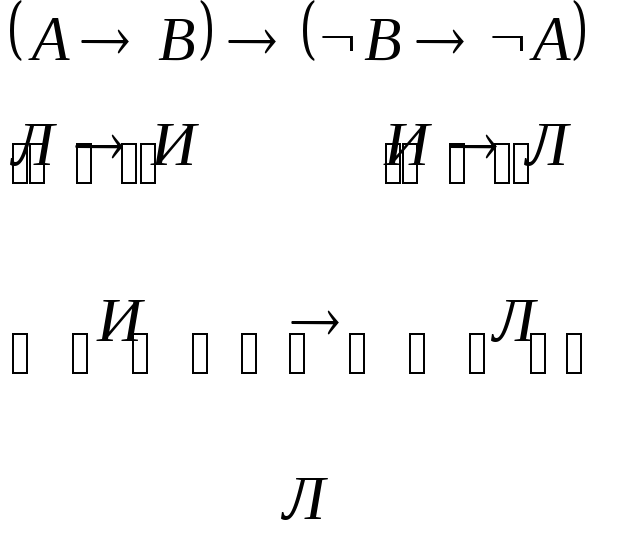
9-ая аксиома не общезначимая ППФ.
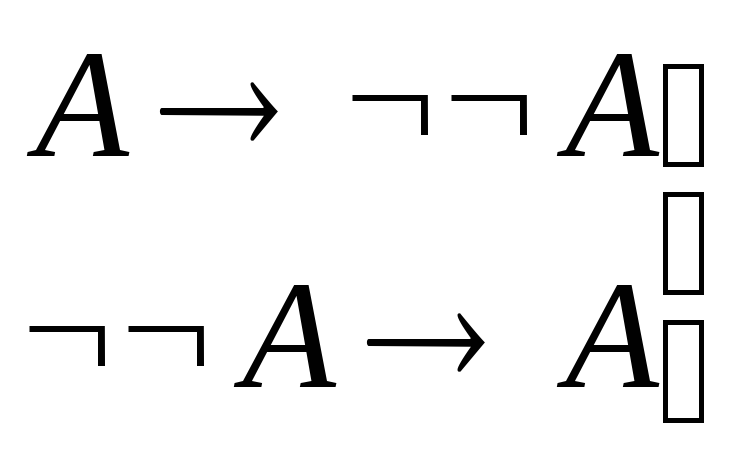 ├
├![]() общезначима.
общезначима.
Основные понятия
логики предикатов (ЛП) I-ого порядка.
До сих пор рассматривали сложные высказывания как простые.
Пусть M
– некоторое множество различных
предметов
![]() ,
высказывание об отдельном предмете
,
высказывание об отдельном предмете
![]() ,
о двух предметах
,
о двух предметах
![]() и нескольких предметах
и нескольких предметах
![]() .
.
Пример.
![]() – 5 – чётное
число (ложь).
– 5 – чётное
число (ложь).
![]() – 4 – чётное число
(истина).
– 4 – чётное число
(истина).
Определение 1.
n-местный
предикат
![]() ,
где
,
где
![]() – предметная переменная.
– предметная переменная.
Предикатом называется логическое высказывание при фиксировании своих аргументов.
Введём две операции:
-
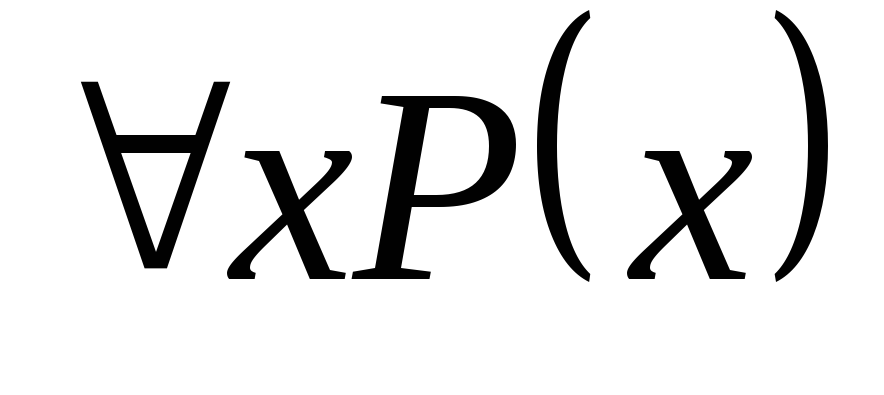 «Все (каждый,
любой) x
обладают свойством P
– истина».
«Все (каждый,
любой) x
обладают свойством P
– истина». -
 «Существует x,
обладающее свойством P
– истина».
«Существует x,
обладающее свойством P
– истина». -



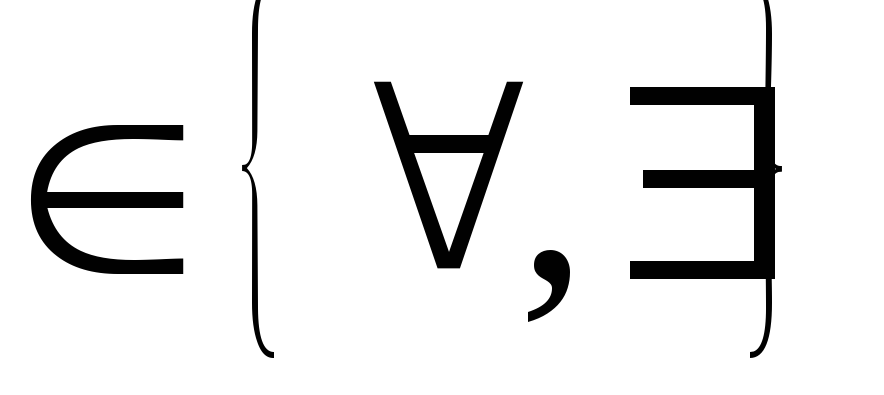
Пусть имеется формула A, тогда в выражении формула А называется областью действия.
Определение 2.
Вхождение x в данную формулу A называется связанным, если x является переменной, стоящей под знаком квантора и находится в области его действия. В противном случае вхождение переменной x свободно.
Определение 3.
Переменная называется свободной (связанной) для данной формулы, если её вхождение в данную формулу свободно (связано).
Пример.
![]() ,
x
– связанная, y
– свободная.
,
x
– связанная, y
– свободная.
В общем случае
![]() понимается как утверждение о том, что
для любых значений, придаваемых переменным
понимается как утверждение о том, что
для любых значений, придаваемых переменным
![]() из области определения, зависит только
от свободных переменных, входящих в
формулу A.
из области определения, зависит только
от свободных переменных, входящих в
формулу A.
Выражение
![]() понимается как утверждение о том, что
существует, по крайней мере, 1 способ
замены переменных
понимается как утверждение о том, что
существует, по крайней мере, 1 способ
замены переменных
![]() своими значениями из области определения
A
такой, что истинность формулы A
будет зависеть только от свободных
переменных, входящих в эту формулу.
своими значениями из области определения
A
такой, что истинность формулы A
будет зависеть только от свободных
переменных, входящих в эту формулу.
Проблемы перевода с естественного языка в логику – основная проблема искусственного интеллекта.
