3. Методичні вказівки до розв’язування задач Теорія масового обслуговування

Для розв'язання цих завдань необхідно уміти розраховувати такі показники системи обслуговування:

1. Можливість того, що в будь-який момент часу усі канали (апарати) виявляться вільними:

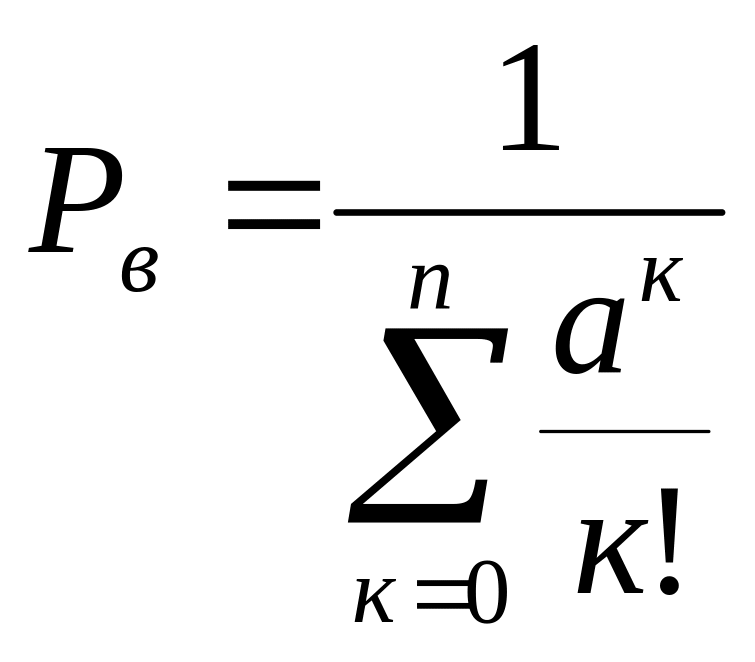
де к - кількість зайнятих каналів;

а - наведена інтенсивність потоку заявок.

2. Середня очікувана кількість вільних каналів:

Ймовірність відмовлення:

.

3. Можливість того, що в будь-який момент часу всі канали виявляться занятими:

.

4. Середньоочікувана кількість зайнятих каналів:

.

5. Коефіцієнт простою каналів:

.

6. Частка завантаження каналів (за час обслуговування):

.

7. Можливість того, що к каналів зайняті:

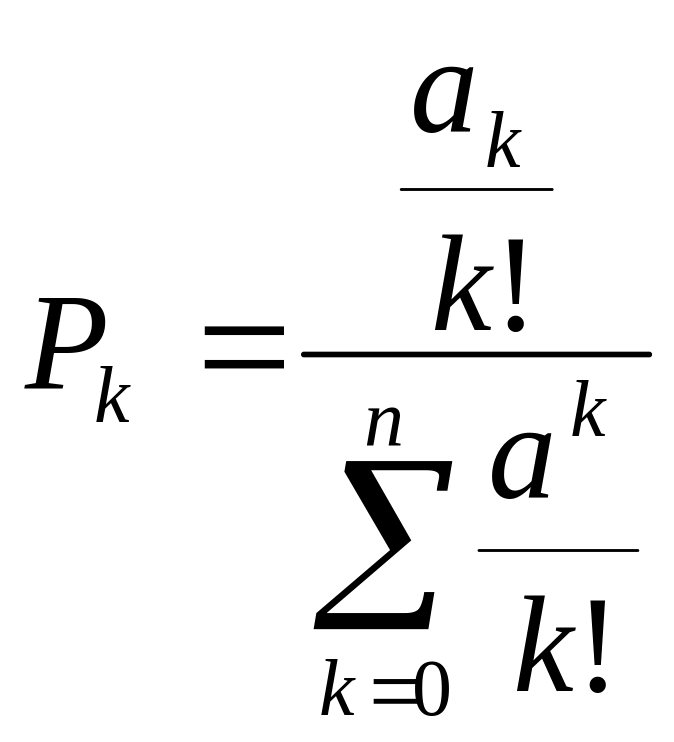, якщо , тоді .

Теорія масового обслуговування використовується при дослідженні операцій. Вона грунтується на методах математики і теорії ймовірностей і розробляє точні способи кількісної оцінки організації масового обслуговування.

Методи теорії розкладів у прийнятті управлінських рішень

Однією з перших математичних моделей теорії розкладів є відома в теорії заощаджень найпростіша модель оптимальної партії поставки, яку можна використати для визначення оптимальної партії випуску виробів. Завдання пов'язані з впорядкуванням операцій. Вони виникають при виборі черговості їх виконання.

Оптимальні параметри моделі:

1. Розмір партії або .

де q – розмір партії; K – накладні витрати, пов’язані з розміщенням замовлення і постачання партії; S – витрати на зберігання продукції за одиницю часу; T – час реалізації проекту; Q – загальні витрати матеріалів; V – середня потреба матеріалів в рік.

2 . Оптимальний інтервал між постачаннями:

або або .

3. Сумарні витрати на формування постачань і зберігання запасів за час будівництва:

або або .

4. Місце розташування замовлення (величина кінцевого запасу, за якого подається замовлення на поповнення):

.

5. Початковий запас, шо гарантує бездефіцитне споживання:

.

Моделі оптимального розміру партії постачання при дефіциті (теорія розкладів):

1. Оптимальна партія постачання знаходиться за формулою:

де d — дефіцит.

1. Максимальна величина заборгованого попиту:

.

3. Оптимальний інтервал між постачаннями:

.

4. Місце розташування замовлення (величина кінцевого запасу, за якого подається замовлення на поповнення):

.

5. Витрати циклу, що включають витрати на розміщення замовлення, зміст запасу і втрати від дефіциту:

.

Методи управління запасами

Основна модель. Найважливішу роль у наших розглядах відіграватиме функція зміни запасів. Це зв'язок між кількістю одиниць товару на складі (потначимо його через Q) і часом t. Вважатимемо, що маємо один вид товару.

Якщо на товар є попит, то функція зміни запасу Q = Q(t) зменшується. Якщо товар, навпаки, завозять на склад, то ця функція зростає. Вважатимемо за можливе миттєве поповнення запасу.

Витрати, що пов'язані із запасами, можна розділити на три частини:

A. Вартість товару.

Б. Організаційні витрати. Це - витрати, пов'язані з оформленням товару, його доставкою, розвантаженням тощо.

В. Витрати на збереження товару. Це - витрати на оренду складу, амортизацію в процесі збереження тощо.

Розглянемо основні величини і припущення відносно них, прийняті в рамках основної моделі. Використовуватимемо як одиницю виміру коштів умовні одиниці (УО); як одиницю виміру часу - рік, хоча можна було б узяти місяць, квартал тощо.

1. Ціна одиниці товару - с. Ціна постійна, розглядається один вид товару.

2. Інтенсивність попиту - d одиниць товару в рік.

3. Організаційні витрати - s за одну партію товару. Вважатимемо, що організаційні витрати не залежать від розміру постачання, тобто від кількості одиниць товару в одній партії.

4. Витрати на збереження запасу - h на одиницю товару в рік. Вважатимемо ці витрати постійними.

5. Розмір однієї партії товару є постійний - q одиниць. Партія надходить миттєво в той момент, коли виникає дефіцит, тобто коли запаси на складі дорівнюють нулю.

Параметри с, d, s, h вважаються заданими і потрібно. Задача управління запасами складається у виборі параметра q в такий спосіб, щоб мінімізувати річні витрати.

Отже, загальні витрати С обчислюються за формулою:

.

Ще раз нагадаємо, що в рамках моделі параметри с, d, s, h вважаються заданими і потрібно знайти таке число q*, щоб функція С=С(q) приймала найменше значення на безлічі q>0 саме в точці q*:

.

Отримана формула називається формулою оптимального запасу, чи формулою Харріса.

Знайшовши оптимальний розмір замовлення, можна визначити оптимальну кількість постачань за рік п* і відповідну тривалість циклу зміни запасу t*:

; днів.

Метод виробничих постачань. В основній моделі передбачалося, що надходження товарів на склад відбувається миттєво. Це припущення достатньо добре відображає ситуацію, коли товар поставляється протягом одного дня (чи ночі). Якщо товари поставляються з працююча виробничої лінії, необхідно модифікувати основну модель. У цьому разі до параметрів с, d, s, h додається ще один - продуктивність виробничої лінії р (одиниць товару в рік). Вважатимемо її заданою і постійною.

Ця нова модель називається моделлю виробничих постачань. Величина q, як і раніше, позначає розмір партії. На початку кожного циклу відбувається "підключення" лінії, що продовжується до нагромадження у одиниць товару. Після цього поповнення не відбувається доти, поки не виник дефіцит.

Загальні витрати С(q), як і в основній моделі, складаються з трьох частин та обчислюються за формулою:

.

Оптимальний розмір постачань q * одержуємо з рівняння:

.

Знайшовши оптимальний розмір замовлення, можна визначити оптимальну кількість постачань за рік п* і відповідні тривалість постачання τ* і тривалість циклу поповнення запасу t*:

; днів; день.

Метод постачань зі знижкою. Розглянемо ситуацію, описувану в цілому основною моделлю, але з однією особливістю, що полягає в тому, що товар можна поставляти за пільговою ціною (зі знижкою), якщо розмір партії досить великий. Іншими словами, якщо розмір партії q є не менший від заданого числа q_о, товар поставляється за ціною с_о, де с_о < с.

Функція загальних витрат С(q) задається в такому випадку у спосіб:

Обидві функції мають мінімум у точці, де .

Для з'ясування питання про те, який розмір партії оптимальний, варто порівняти значення функції С(q) у точці і та точка, де функція С(q) приймає менше значення, буде оптимальним розміром партії у моделі постачань зі знижкою.